化妆品网站建设规模设想刷排名的软件是什么
有时候我们在导入项目,如果手动在IDEA中指定jdk版本,往往启动项目会报错误。
因此当我们新引入项目启动不了时可以检查一下自己IDEA中的jdk版本是否正确。
下面以配置jdk版本为11显示步骤:
1、配置 Project Structure
1.1、通过快捷键"ctrl+shift+alt+s" 打开Project Structure配置面板或者点击这个按钮。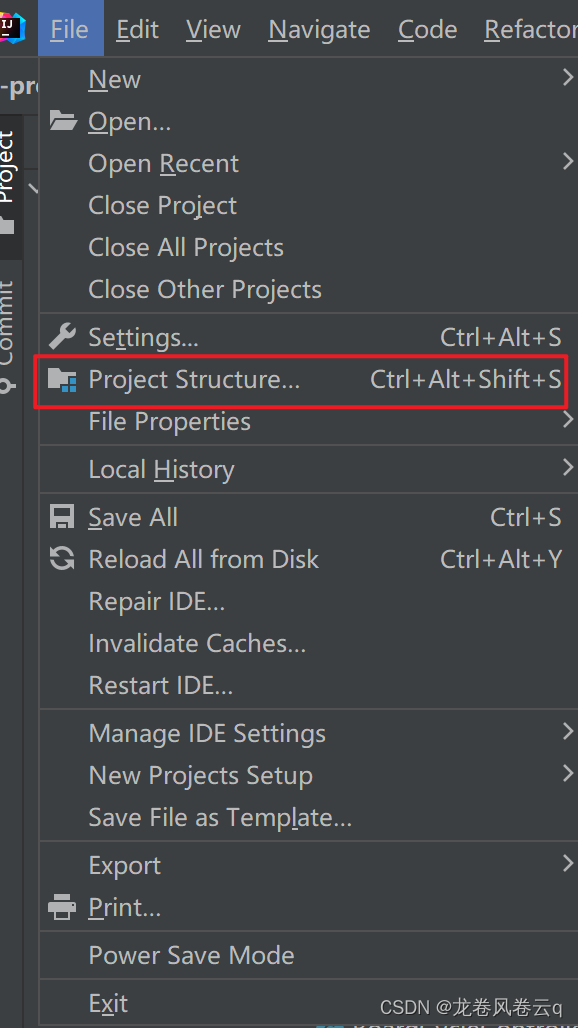
1.2、配置Project -> Project SDK为JDK11。

1.3、配置Project -> Project language level为11。

1.4、配置Modules -> Sources -> Language level为11。
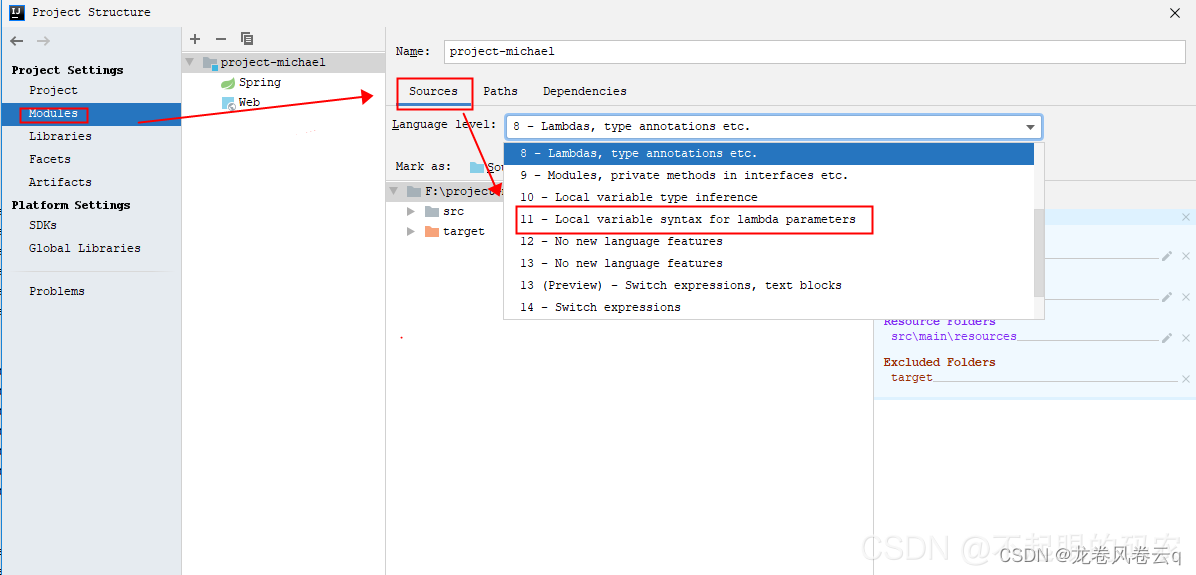
1.5、配置Modules -> Dependencies ->Module SDK为JDK11。
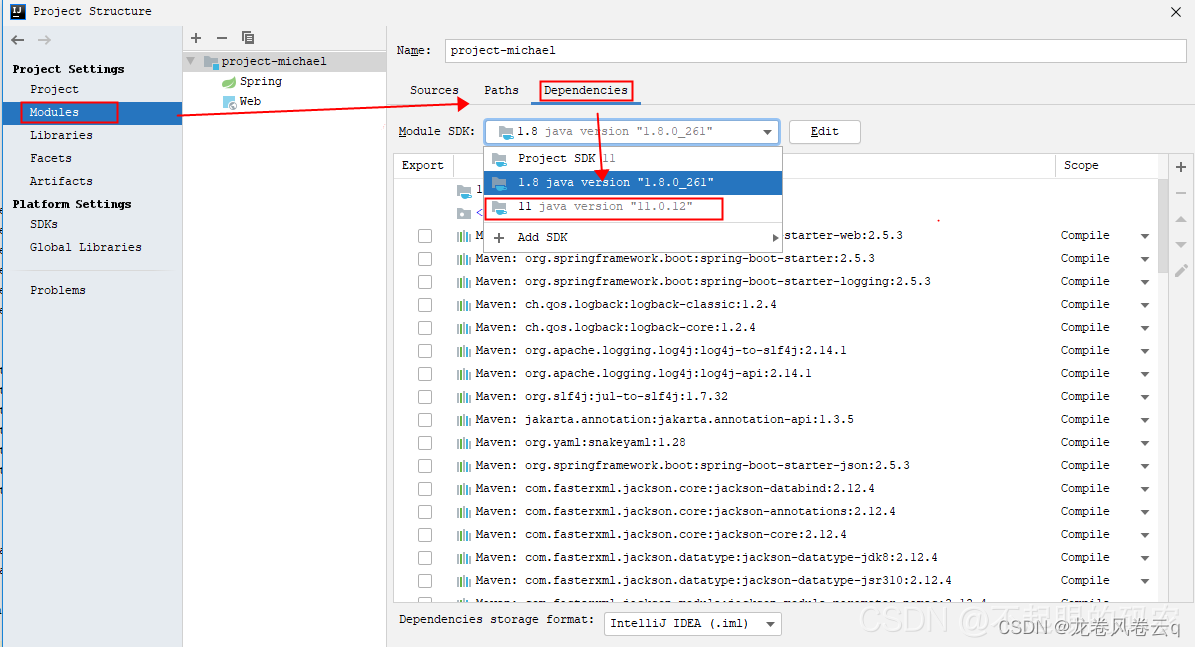
1.6、在SDKs中,选择11。

2、配置 Settings
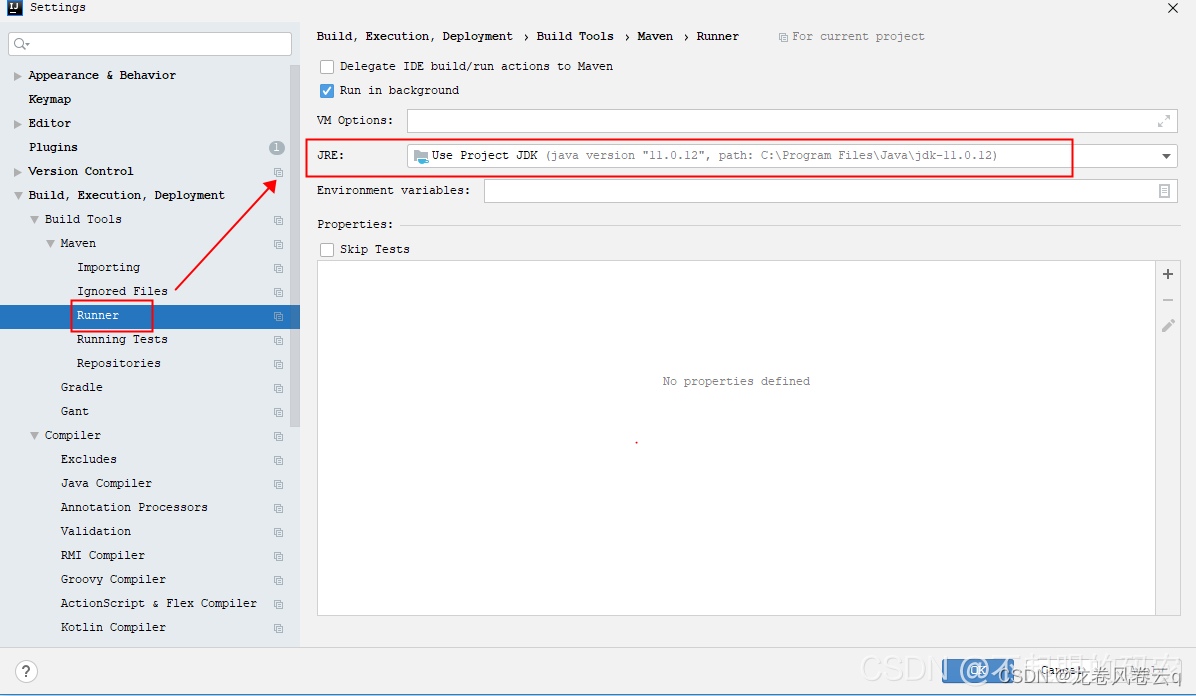
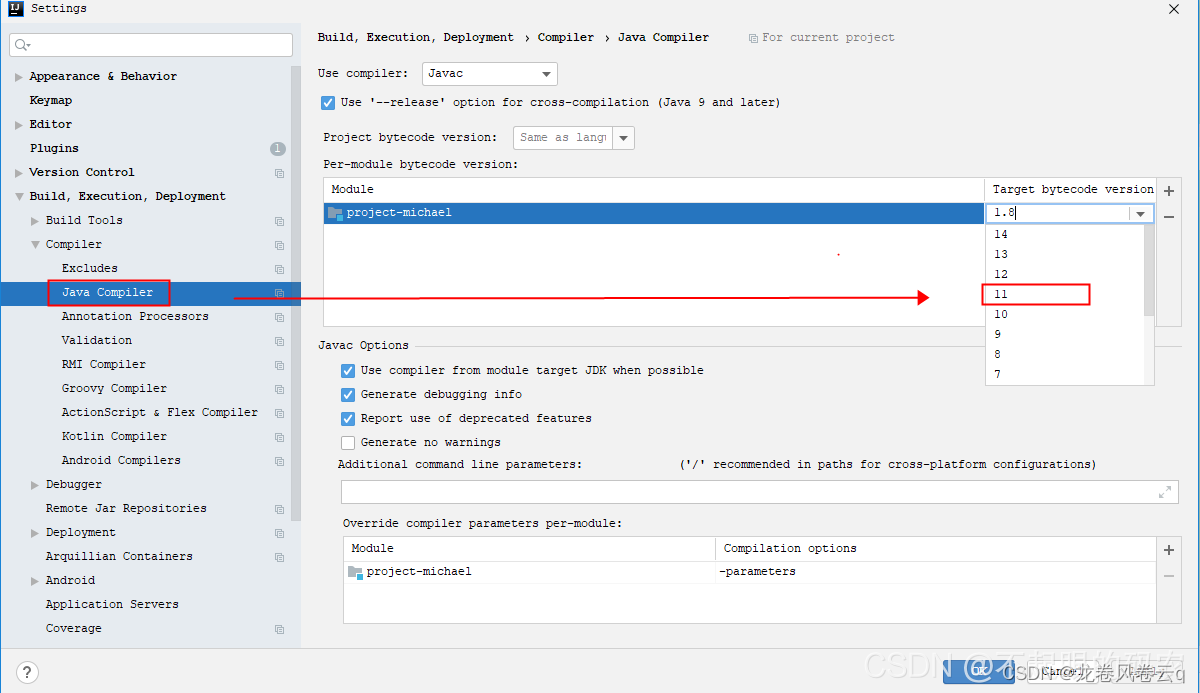
2.1、File -> Settings…打开Settings配置界面,配置以下内容,不多说了,直接上图。