做一个购物网站怎么找关键词
1、如何像windows一样看磁盘?
不断的在上层文件夹显示,找到最上层,拖拽到左侧,方便之后找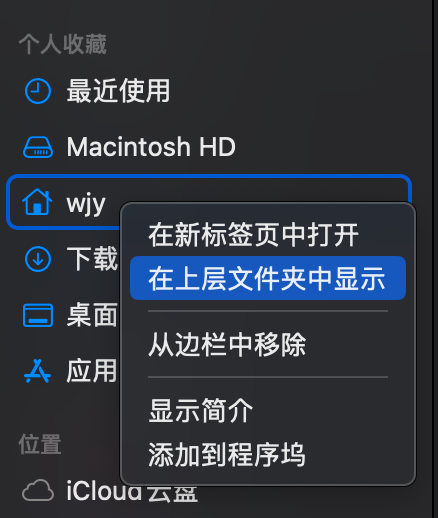
2、Macintosh HD显示隐藏文件夹方法
终端窗口:
defaults write com.apple.finder AppleShowAllFiles true
killall Finder
或者:按住 Shift + Command + .(点号键)
3、如果打开一个程序时候显示:无法打开“clickhouse-macos”,因为无法验证开发者
那么在finder找到这个文件,接着按着control,点确定打开即可
4、如何查看HomeBrew是否安装了某个程序?
brew list
5、查看这个程序的位置:
brew info 程序名
6、添加环境变量
举个例子:
添加 ClickHouse 可执行文件路径到环境变量:
打开终端,并编辑您的 shell 配置文件(例如 ~/.zshrc)。
添加以下行到文件中,将 <clickhouse_bin_path> 替换为 ClickHouse 可执行文件的路径(从上一步获得):
Copy
export PATH=“<clickhouse_bin_path>:$PATH”
保存文件并关闭编辑器。
在终端中运行 source ~/.zshrc 命令,以使更改生效。
资料来源:poe-chatGPT
