触屏版网站css网络推广费用计入什么科目
应用层
再谈 "协议"
协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢?
为什么要转换呢?
如果我们将struct message里面的信息分别作为独立的内容将这个4个信息分别传过去可以吗?
什么是序列化和反序列化?
为什么需要进行序列化和反序列化?
我们之前的tcp,udp通信,有没有进行任何的序列化和反序列化呢?
如何进行序列化和反序列化呢?
网络版计算器
Sock.hpp
CalServer.cc
CalClient.cc
测试结果
存在的问题
json
如何进行序列化和反序列化?
json的使用
序列化
反序列化
我们对计算器进行优化(内置序列化和反序列化)
Protocol.hpp
Makefile
CalServer.cc
CalClient.cc
测试:
对网络计算器的总结
HTTP协议
认识URL
url字段解析
urlencode和urldecode
转义的规则如下
HTTP协议格式
HTTP请求
请求行
请求报头
空行
请求正文
如何理解普通用户的上网行为?
http的响应
状态行
响应报头
空行
响应正文
请求与响应的整体格式
http request和http response 被如何看待?
如何解包和封包呢?
如何分用?
HTTP操作
http中面向字节流读的函数recv
最简单的HTTP服务器
测试
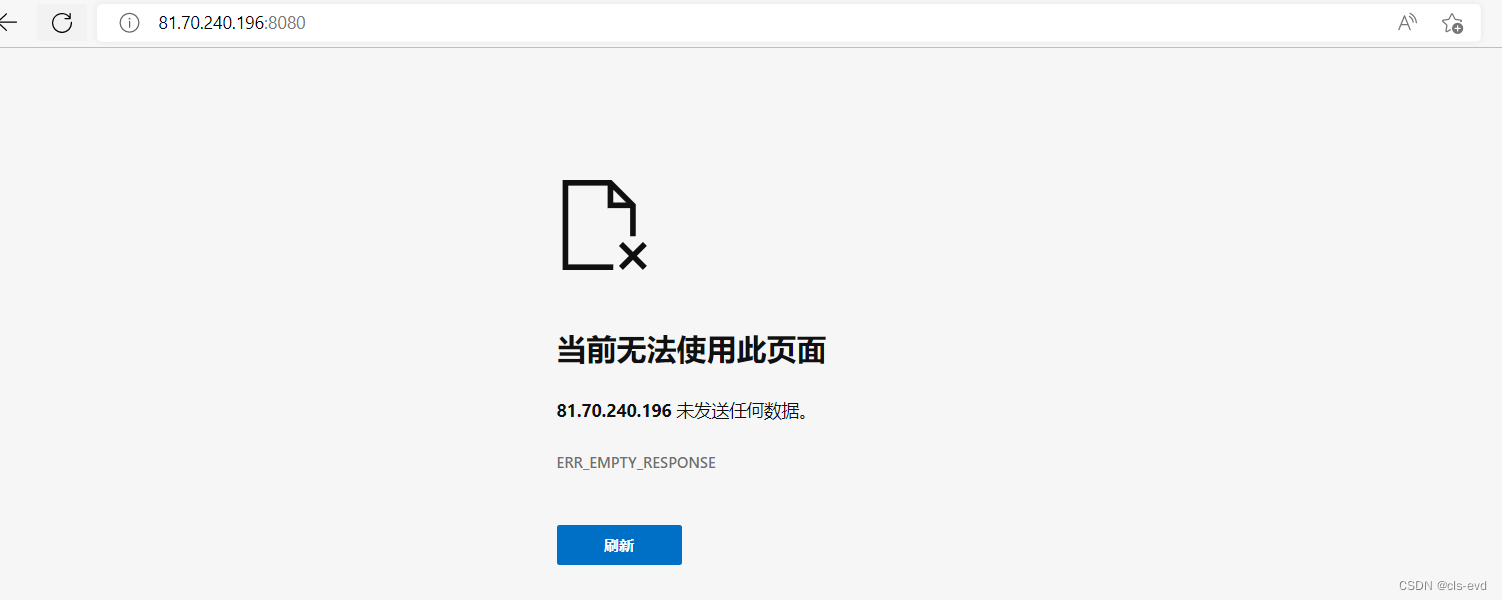
为什么客户端发了多条请求呢?
HTTP请求
这个http的请求和响应为什么都带了版本呢?
对于HTTP请求的报头字段的解释
服务器构建响应
send
Sock.hpp
HTTP.cc
测试
HTTP的请求与响应总结
观察百度的网页
再谈http请求的细节
HTTP请求
理解Content-Length
读取要求
你怎么保证你每次读到的是一个完整的http呢?
假设有正文的话,你如何知道空行之后有多少个字符呢?
如何读到一个完整的http协议?
HTTP响应
HTTP的请求方法
短链接
早期的http1.0为什么用短链接呢?
HTTP的方法
/ (根目录)
实验
响应报头部分
响应正文
完整代码
测试:
验证GET和POST方法
GET方法
html的表单
制作表单
POST方法
GET和POST的区别
通过抓包观察GET与POST
抓包的原理
fiddler查看POST 方法
fiddler查看GET
GET和PSOT
概念问题
区别
如何选择
所谓的文本分析
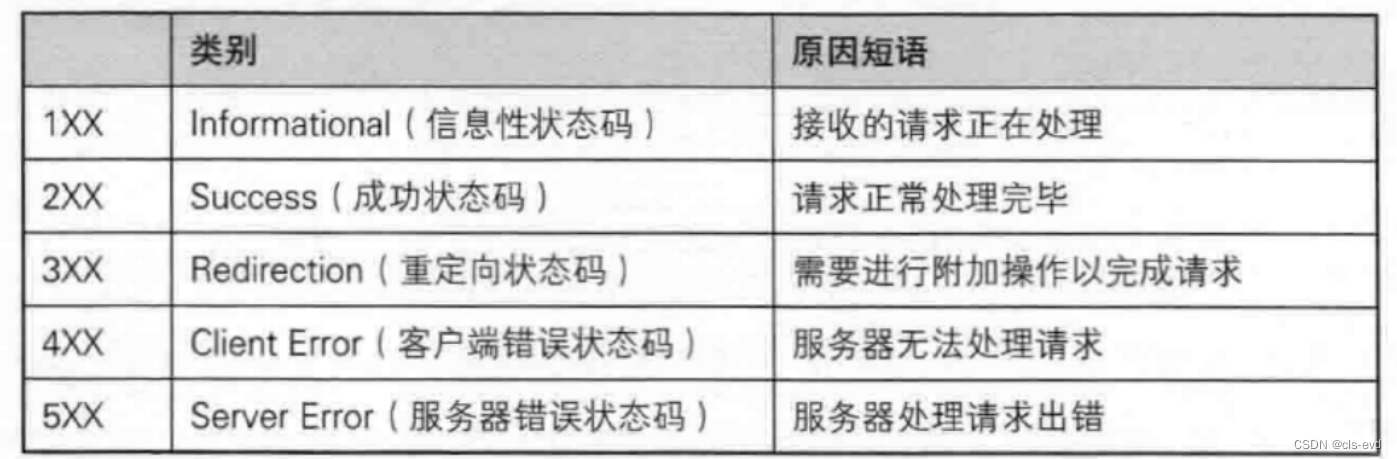
HTTP常见的状态码
具有指导意义的状态码
404的错误属于客户端问题,还是服务器问题?
服务器的问题有哪些呢?
3开头的状态码
重定向是什么?
什么叫做永久重定向,什么叫做临时重定向?
模拟重定向
测试302,临时重定向
永久重定向遗留的问题
再谈HTTP常见Header
长连接与短连接
短连接
长连接
Connection
背景引入
问题引入
Cookie
对我们来讲,http是不记录上下文的是无状态的,那网站是如何认识我的呢?
会话与会话管理
session
为什么私密信息会被盗取呢?
session处理策略
再谈http无状态
为什么网站需要认证用户,也就是为什么登录这个网站的时候它需要永久的认识用户呢?
HTTPS
背景认识一
背景认识二(数据的加密方式)
1.对称加密
2.非对称加密
背景认识三
假设现在有一篇论文,那么如何防止文本中的内容被篡改?以及识别到是否被篡改?
我是一个通信端,我现在要发送这段文本,我怎么保证这段文本没有被篡改?
校验
https是如何通信的呢
如何选择加密算法
方案一
方案二
对称加密
非对称加密
两对非对称秘钥的问题
实际中的加密方法
什么叫做安全
中间人
那么在服务端把公钥给客户端的时候,可不可能出现问题呢?
证书
证书是什么
CA机构
创建证书
有了证书后,请求该怎么做呢?
编辑数字签名中间人改不了吗?
如果中间人也是一个合法的服务方呢?
客户端是如何知道CA机构的公钥信息呢?
应用层
我们程序员写的一个个解决我们实际问题, 满足我们日常需求的网络程序, 都是在应用层.
再谈 "协议"
协议是一种 "约定". socket api的接口, 在读写数据时, 都是按 "字符串" 的方式来发送接收的. 如果我们要传输一些"结构化的数据" 怎么办呢?

这就是曾经我们在写C/C++定义出来的对象,我们要把它发出。我们要把数据发送到网络当中,肯定不是直接就把这样的结构化数据放到网络里传过去让对方收到。因为这些消息里,大家的大小,长度,都是变长的,都是不一样的,所以我们在实际发给对方的时候,是不方便统一发送的,那我们实际上就需要把这里的各种结构化信息,我们要把它转化成一个长的“字符串”(实际上应该转化成一个长的字节流或者数据包发出去)
为什么要转换呢?
我们的message是一个结构体,之前我们存在一个概念是结构体的内存对齐,那么如果我是一个message,那么将来你接收的时候,也一定是struct message。但是发送方和接收方的message的大小不一定一样,其中双方里面字段开辟的长度也都不一定一样。所以直接把信息传过去这种做法是不正确的。我们需要将其转化成一个长字符串。
如果我们将struct message里面的信息分别作为独立的内容将这个4个信息分别传过去可以吗?
从技术实现上,如果你想分别传过去,这个时候每一个信息就是一个独立的信息,整体就不是结构化数据了,因为这样成本太高了,假如有成百上千的人给我们这样单独的一条一条发信息,那么我们最后还得组合区分,哪几条是组合在一起的。所以我们一般不会这么做,我们需要将它转换成对应的长字符串,也就是把它打包。
什么是序列化和反序列化?
所以我们要把这种结构化的数据,转化成某种长字符串的信息,传递给对方,对方在根据这里的长字符串,以此定义一个message对象,然后将数据由一个字符串转化成一个结构化的数据。其中我们把从结构化数据转换成长字符串的过程我们就叫做序列化的过程。当我们把长字符串转化上来的时候 ,新的结构体里面就会有各种信息,这些信息我们再由我们的分析算法,把字符串里面的内容在一个个的分析出来,然后填入到结构体当中,在形成一个新的结构化的数据,这个过程我们称之为反序列化的过程。
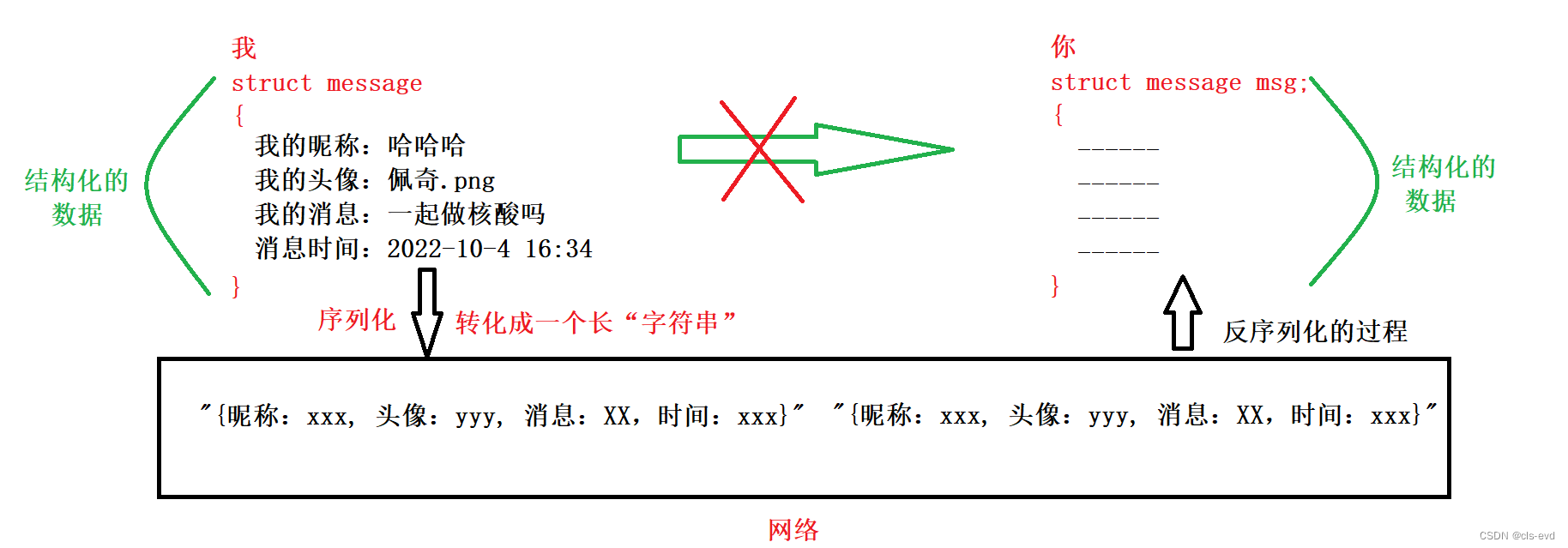 说白了就是我们要将结构化的数据转换成字符串,然后再将字符串反序列化变成结构化的数据,这是我们在网络通信里必须得做的。
说白了就是我们要将结构化的数据转换成字符串,然后再将字符串反序列化变成结构化的数据,这是我们在网络通信里必须得做的。
为什么需要进行序列化和反序列化?
答:1.这种结构化的数据是不便于网络传输的。结构化的数据在网络上不好传输,但我把整个对象转成一个字符串,字符串里面包含了你的每一个字段的信息,到了对方以后,我再把字段的信息一个个提出来形成一个对象,整个就是序列化和返反序列化的过程。字符串便于网络传输。归根结底就是为了应用层网络通信的方便。
2.序列和反序列化不是目的,在我们两个人的上层,还有其他应用,比如,图形界面显示要拿你的昵称,头像,消息,时间,因为是结构化的数据,所以我们可以用类名+方法就把他的属性拿到了。如果我们在对端,只拿这个字符串去用,上层就需要把这个字符串解析的工作全部由我们自己再次完成,这太麻烦了,所以我们先反序列化得到结构化的数据,就方便我们一次一次的向上层去拿。总结:为了方便上层进行使用内部成员,将应用和网络进行了解耦!应用压根不关心网络发送,作为应用我只关心,结构体数据里的成员,结构化的数据怎么在网络里传输,如何序列化和反序列化,应用层压根不关心。这就完成了解耦。
我们之前的tcp,udp通信,有没有进行任何的序列化和反序列化呢?
压根就没有,原因就是我们没有应用场景,我们不知道我们要干什么,我们就不知道应用场景是什么,就没办法定制序列和反序列化的一些结构化数据,也就不需要字符串的序列和反序列化的过程,所以之前我们并没有。
这里结构化的数据本质就是协议的表现,就好比QQ软件就知道昵称对应的信息是什么样子的,头像是连接还是文件,时间是以什么格式展示的...这就叫做协议
如何进行序列化和反序列化呢?
像xml,json,protobuff就是专门用来负责做序列化和反序列化这样的过程的。
网络版计算器
目的: 我们需要实现一个服务器版的加法器. 我们需要客户端把要计算的两个加数发过去, 然后由服务器进行计算, 最后再把结果返回给客户端.
约定方案一:
- 客户端发送一个形如"1+1"的字符串;
- 这个字符串中有两个操作数, 都是整形;
- 两个数字之间会有一个字符是运算符, 运算符只能是 + ;
- 数字和运算符之间没有空格;
- ...
这就是约定,当客户端发送一个数据的时候,服务端立马就意识到,它一定有操作数和操作符,而且操作符左右两侧一定是数据没有空格,所以服务端收到1+1这样的字符串,就需要根据操作符把1和1解开。
我们这样去做的伪代码
这个过程是比较麻烦的,这个序列化和反序列化动作都是由我们自己做的
约定方案二:
- 定义结构体来表示我们需要交互的信息; (结构化的数据)
- 发送数据时将这个结构体按照一个规则转换成字符串, 接收到数据的时候再按照相同的规则把字符串转化回结构体;
- 这个过程叫做 "序列化" 和 "反序列化"
这种方式,发的时候发了一个结构体,收的时候也收了一个结构体,因为他俩成员一样,一旦收到内容后,就直接可以在上层拿到内容了。但是这种方式存在问题,因为这种方式是语言的特性做了序列化和反序列化,但是不太推荐。
我们接下来,就实现一个网络版本的计算器,我们利用约定方案二进行实现
Protocol.hpp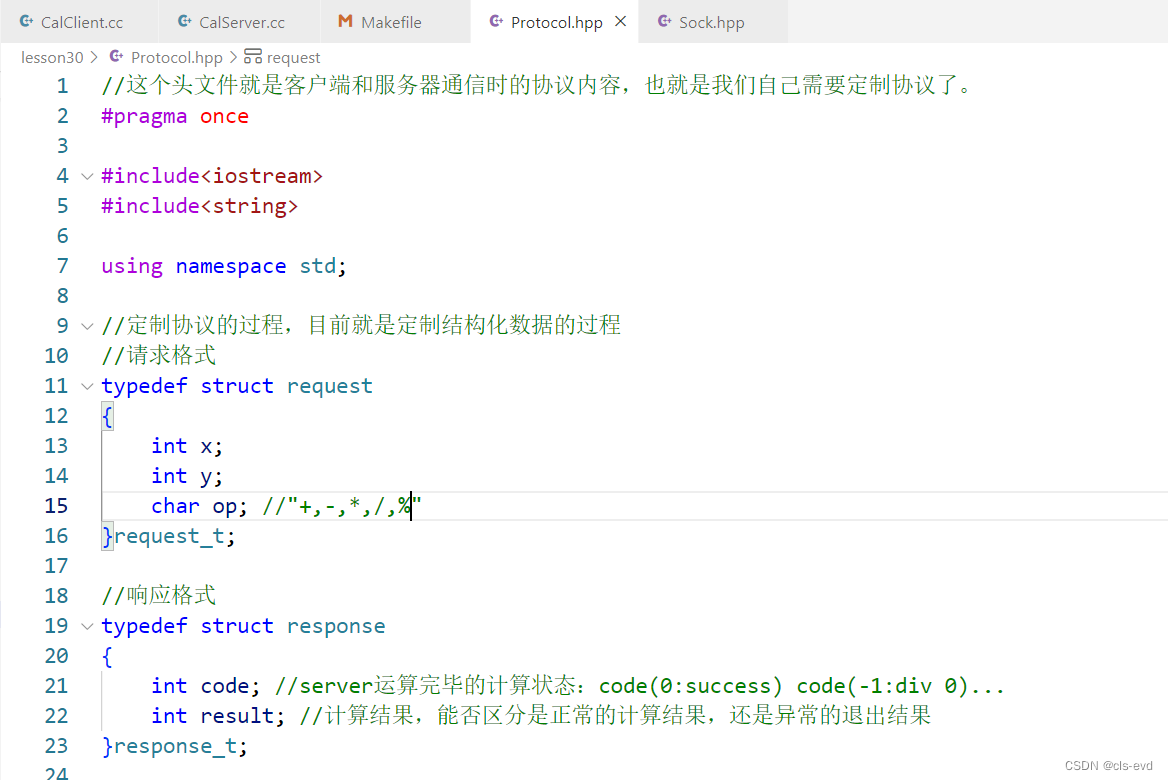
因为存在10/0或者10%0这样的错误操作,所以我们需要一个code代表运算完毕的状态。换言之,我将来想要拿到退出结果的时候,我们要做的第一件事情是先检查code,只有code是0的时候,result才有意义,否则result是没有意义的。
以上就定制好了我们的协议(双方通信时采用的数据格式),我们发的一定是request这种数据格式,收的一定是response这种格式,上面的这两种数据就叫做结构化数据,我们发的时候可以把request定义的对象直接发过去,但是这样发存在问题,客户端和服务器对于结构体的大小可能不一样,而且不同平台的大小也不一样,eg:这里的结构体里面用的是整形,有一天你将客户端发出去了,服务器升级了,一个int占64个比特位,这样的话客户端发过来的数据结构体大小就匹配不上了,就出问题了。所以我们需要序列化和反序列化的。
做一个套接字接口的封装
Sock.hpp
#pragma once#include<iostream>
#include<string>
#include<cstring>
#include<cstdlib>
#include<sys/socket.h>
#include<netinet/in.h>
#include<arpa/inet.h>
#include<unistd.h>using namespace std;
class Sock
{
public:static int Socket(){int sock = socket(AF_INET, SOCK_STREAM, 0);if (sock < 0){cerr << "socket error" << endl;exit(2); //直接终止进程}return sock;}static void Bind(int sock,uint16_t port){struct sockaddr_in local;local.sin_family = AF_INET;local.sin_port = htons(port);local.sin_addr.s_addr = INADDR_ANY;if (bind(sock, (struct sockaddr *)&local, sizeof(local)) < 0){cerr<<"bind error!"<<endl;exit(3);}}static void Listen(int sock){if (listen(sock, 5) < 0){cerr << "listen error !" << endl;exit(4);}}static int Accept(int sock){struct sockaddr_in peer;socklen_t len = sizeof(peer);int fd = accept(sock, (struct sockaddr *)&peer, &len);if (fd >= 0){return fd;}return -1;}static void Connect(int sock, std::string ip, uint16_t port){struct sockaddr_in server;memset(&server, 0, sizeof(server));server.sin_family = AF_INET;server.sin_port = htons(port);server.sin_addr.s_addr = inet_addr(ip.c_str());if (connect(sock, (struct sockaddr*)&server, sizeof(server)) == 0){cout << "Connect Success!" << endl;}else{cout << "Connect Failed!" << endl;exit(5);}}
};CalServer.cc
#include"Protocol.hpp"
#include"Sock.hpp"
#include<pthread.h>
static void Usage(string proc)
{cout << "Usage: " << proc << "port" << endl;exit(1);
}void* HandlerRequest(void* args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());//version1 原生方法,没有明显的序列化和反序列化的过程//业务逻辑,做一个短服务 request -> 分析处理 -> 构建response ->sent(response) ->close(sock)//1.读取请求request_t req;ssize_t s = read(sock, &req, sizeof(req));if (s == sizeof(req)){//读取到了完整的请求,待定//req.x,req.y,req.op// 2.分析请求 && 3.计算结果response_t resp = {0, 0}; //响应,默认设置0,0// 4.构建响应,并进行返回switch (req.op){case '+':resp.result = req.x + req.y;break;case '-':resp.result = req.x - req.y;break;case '*':resp.result = req.x * req.y;break;case '/':if (req.y == 0){resp.code = -1; //代表除0}else{resp.result = req.x / req.y;}break;case '%':if (req.y == 0){resp.code = -2; //代表模0}else{resp.result = req.x % req.y;}break;default:resp.code = -3; //代表请求方法异常break;}cout << "request: " << req.x << req.op << req.y << endl; write(sock, &resp, sizeof(resp));cout << "服务结束" << endl;}//5.关闭连接close(sock);
}// ./CalServer port
int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){cout << "get a new client..." << endl;int *pram = new int(sock);pthread_t tid;pthread_create(&tid, nullptr, HandlerRequest, pram);}}return 0;
}CalClient.cc
#include "Protocol.hpp"
#include "Sock.hpp"void Usage(string proc)
{cout << "Usage: " << proc << " server_ip server_port " << endl;
}//./CalClient server_ip server_port
int main(int argc, char *argv[])
{if (argc != 3){Usage(argv[0]);exit(1);}int sock = Sock::Socket();Sock::Connect(sock, argv[1], atoi(argv[2]));//业务逻辑request_t req;memset(&req, 0, sizeof(req));cout << "Please Enter Date One# ";cin >> req.x;cout << "Please Enter Date Two# ";cin >> req.y;cout << "Please Enter operator# ";cin >> req.op;ssize_t s = write(sock, &req, sizeof(req));response_t resp;s = read(sock, &resp, sizeof(resp));if (s == sizeof(resp)){cout << "code[0:success]: " << resp.code << endl;cout << "result: " << resp.result << endl;}return 0;
}测试结果
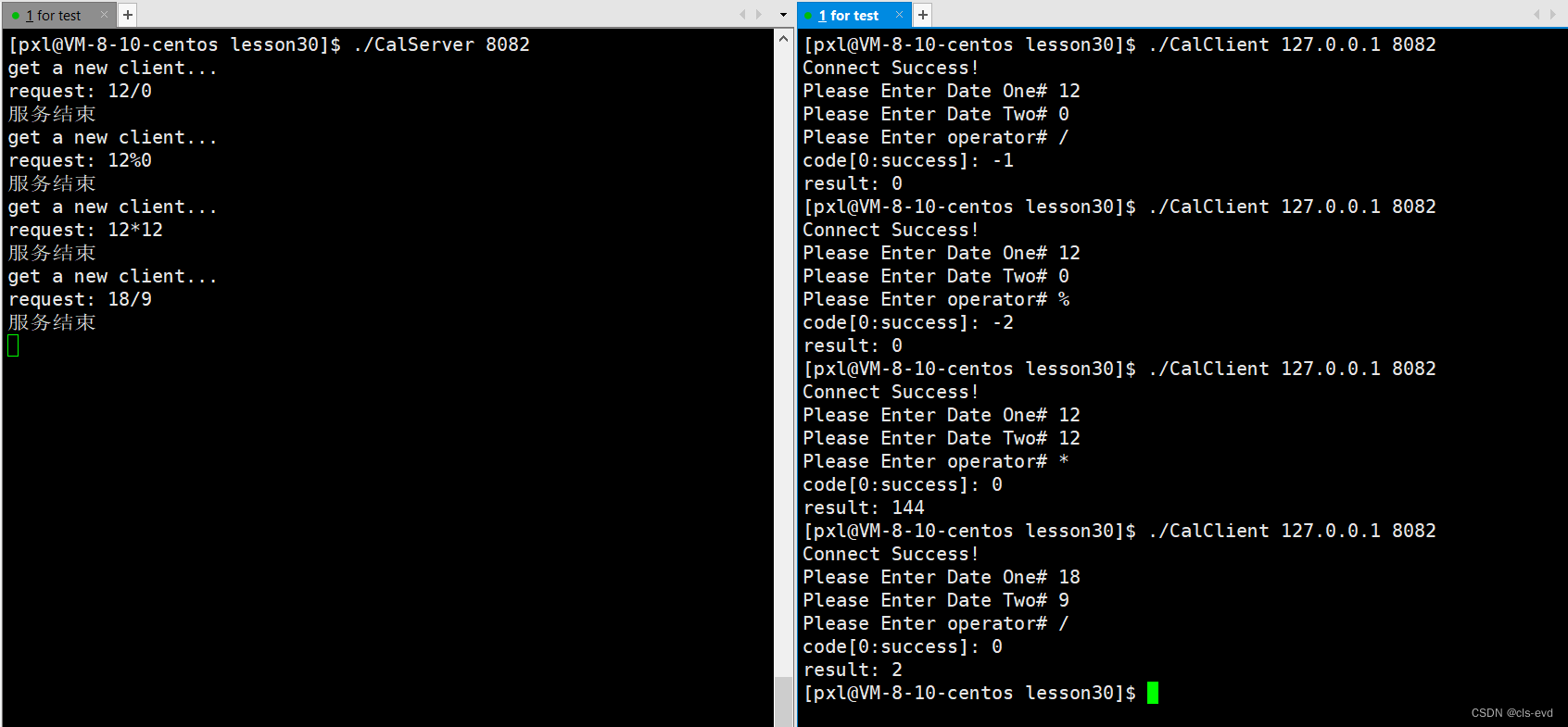
ps:如果你想改成长服务,你就需要在服务端,把刚刚做的那一批请求包裹在死循环中就可以了。
服务器怎么知道是x op y 呢?服务器怎么知道,op的+,-,*,/,%是什么含义呢?服务器怎么知道,code为0,1,2,3的意思呢?我怎么知道,客户端和服务器又怎么知道?
这就叫做约定,所以我们刚刚用结构化的数据,又结合我们自己的约定,然后我们就定义了一个简单的协议,这就叫做约定。
存在的问题
我们今天的协议逻辑上是没有问题的,不过如果客户和服务器使用这样的原生结构体的方式,发送二进制数据的内容(一个结构化的数据发过去到对方),事实证明这样是行的。但是能起效果,仅仅会满足90% 的情况。当我们正常通信的时候,客户端和服务器如果软件版本是迭代的,那么如果现在你有一个老的客户端,你用这样的方式,比如以前结构体的内存对齐方式,结构体的大小,使用的是标准A,后来经过5年,10年的发展,计算机不断进步,内存对齐的方式变得和之前不一样了,客户端已经发给客户了,那么作为客户来讲,客户就喜欢老东西,就喜欢老的客户端,但你的服务器早就升级成了很高很高的版本,那么当客户端发来消息的时候,那么如果哪怕有一个字节发生变化,那你的协议就跑不起来了。所以这样的方案并不好,而且并不适合后序大型的业务处理。在应用层,这种结构化的数据直接发,虽然在我们目前看来可行,但我们不建议,因为我们少了序列化和反序列化的步骤。
json
如何进行序列化和反序列化?
jsoncpp是C++当中使用频率很高的一个进行序列化和反序列化的一个组件。
云服务器通过该条指令进行安装
sudo yum install -y jsoncpp-devel这条命令就是安装我们的开发包。
安装完毕。

这就是我们安装的json,安装一个库说白了就是安装一堆对应头文件,和它对应的一堆库,我们就可以直接使用这个库了。
json的使用
序列化
#include<iostream>
#include<string>
#include<jsoncpp/json/json.h>typedef struct request
{int x;int y;char op;
}request_t;int main()
{request_t req = {10, 20, '*'};//进行序列化Json::Value root; //可以承装任何对象,json是一种kv式的序列化方案root["datax"] = req.x;root["datay"] = req.y;root["operator"] = req.op;//FastWriter, StyledWriterJson::StyledWriter writer;std::string json_string = writer.write(root);std::cout << json_string << std::endl;return 0;
}执行结果:编译的时候要指明链接的动态库
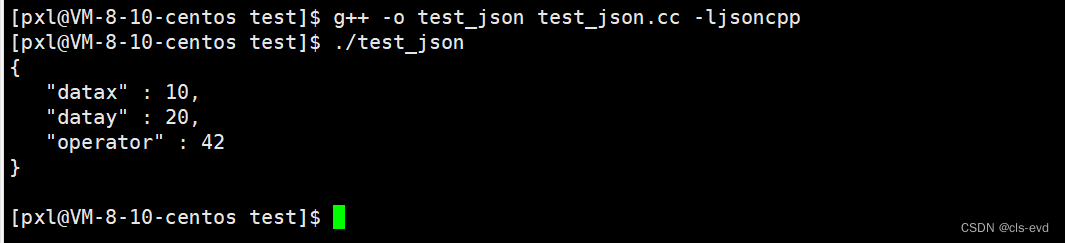
此时我们就形成了一个序列化的结果,有人说这不还是结构化的数据吗,事实上已经完成不一样了,我们自己写的结构体是一个二进制的数据,也就是内存是什么样子,网络里就是什么样子,但我们的运行结果是一个字符串的数据。
我们将StyledWriter改为FastWriter,我们再次运行。
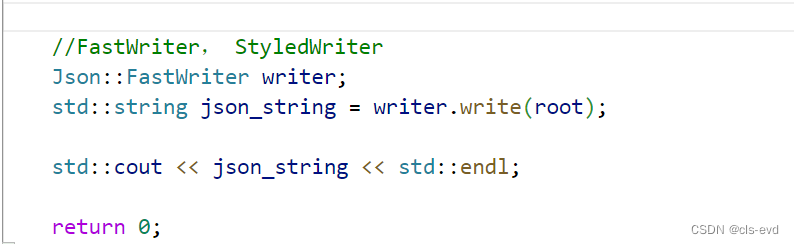
 这个时候得到的就像一个字符串了(实际上人家就是一个字符串),其中每一个字段,datax就是10,datay是20,operator是42(*的ASCII是42),这就是一种kv的方案。这就是序列化的过程,我们通过网络发送的不是我们自己定义的结构体,发送的是我们的运行结果。
这个时候得到的就像一个字符串了(实际上人家就是一个字符串),其中每一个字段,datax就是10,datay是20,operator是42(*的ASCII是42),这就是一种kv的方案。这就是序列化的过程,我们通过网络发送的不是我们自己定义的结构体,发送的是我们的运行结果。
反序列化
序列化是把结构化的数据转换成一个字符串,反序列化的目的就是把一个字符串转换成一个结构化的数据。
运行结果:
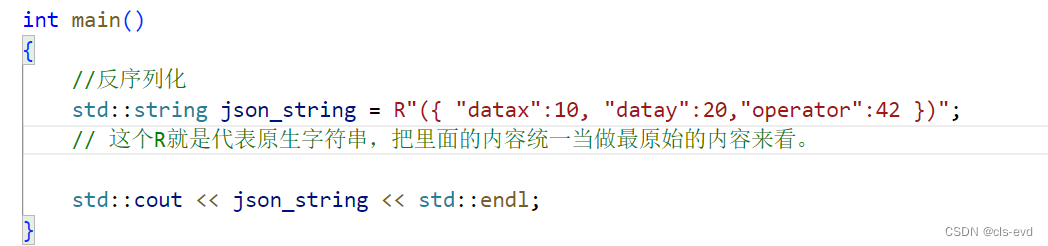
ps:关于R
新的C++标准可以在代码里嵌入一段原始字符串,该原始字符串不作任何转义,所见即所得,这个特性对于编写代码时要输入多行字符串,或者含引号的字符串提供了巨大方便。
先介绍特性如下:
原始字符串的开始符号 :R"( , 原始字符串的结束符号:)"。R" 与 ( 之间可以插入其它任意字符串。
eg2:
int main()
{//反序列化std::string json_string = R"({ "datax":10, "datay":20,"operator":42 })";// 这个R就是代表原生字符串,把里面的内容统一当做最原始的内容来看。 Json::Reader reader;Json::Value root;reader.parse(json_string, root);request_t req;req.x = root["datax"].asInt();req.y = root["datay"].asInt();req.op = (char)root["operator"].asInt();std::cout << req.x << " " << req.op << " " << req.y << std::endl;
}执行结果:

我们对计算器进行优化(内置序列化和反序列化)
Protocol.hpp
//这个头文件就是客户端和服务器通信时的协议内容,也就是我们自己需要定制协议了。
#pragma once#include<iostream>
#include<string>
#include<jsoncpp/json/json.h>using namespace std;//定制协议的过程,目前就是定制结构化数据的过程
//请求格式
//我们自己定义的协议,client&&server都必须遵守!这就叫做自定义协议。
typedef struct request
{int x;int y;char op; //"+,-,*,/,%"
}request_t;//响应格式
typedef struct response
{int code; //server运算完毕的计算状态:code(0:success) code(-1:div 0)...int result; //计算结果,能否区分是正常的计算结果,还是异常的退出结果
}response_t;//序列化 request_t -> string
std::string SerializeRequest(const request_t &req)
{Json::Value root; //可以承装任何对象,json是一种kv式的序列化方案root["datax"] = req.x;root["datay"] = req.y;root["operator"] = req.op;// FastWriter, StyledWriterJson::FastWriter writer;std::string json_string = writer.write(root);return json_string;
}//反序列化 string -> request_t
void DeserializeRequest(const std::string &json_string,request_t &out)
{Json::Reader reader;Json::Value root;reader.parse(json_string, root); out.x = root["datax"].asInt();out.y = root["datay"].asInt();out.op = (char)root["operator"].asInt();}std::string SerializeResponse(const response_t &resp)
{Json::Value root;root["code"] = resp.code;root["result"] = resp.result;Json::FastWriter writer;std::string res = writer.write(root);return res;
}void DeserializeRequest(const std::string &json_string, response_t &out)
{Json::Reader reader;Json::Value root;reader.parse(json_string, root);out.code = root["code"].asInt();out.result = root["result"].asInt();
}Makefile
.PHONY:allall: CalClient CalServerCalClient:CalClient.cc g++ -o $@ $^ -std=c++11 -ljsoncppCalServer:CalServer.cc g++ -o $@ $^ -std=c++11 -lpthread -ljsoncpp.PHONY:clean
clean:rm -rf CalClient CalServerCalServer.cc
#include "Protocol.hpp"
#include "Sock.hpp"
#include <pthread.h>
static void Usage(string proc)
{cout << "Usage: " << proc << "port" << endl;exit(1);
}void *HandlerRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());// version1 原生方法,没有明显的序列化和反序列化的过程//业务逻辑,做一个短服务 request -> 分析处理 -> 构建response ->sent(response) ->close(sock)// 1.读取请求char buffer[1024];request_t req;ssize_t s = read(sock, buffer, sizeof(buffer) - 1); //读到buffer里面if (s > 0){buffer[s] = 0;cout << "get a new request: " << buffer << std::endl; //看到反序列化之前的结果std::string str = buffer;DeserializeRequest(str, req); //反序列化请求//读取到了完整的请求,待定// req.x,req.y,req.op// 2.分析请求 && 3.计算结果response_t resp = {0, 0}; //响应,默认设置0,0// 4.构建响应,并进行返回switch (req.op){case '+':resp.result = req.x + req.y;break;case '-':resp.result = req.x - req.y;break;case '*':resp.result = req.x * req.y;break;case '/':if (req.y == 0){resp.code = -1; //代表除0}else{resp.result = req.x / req.y;}break;case '%':if (req.y == 0){resp.code = -2; //代表模0}else{resp.result = req.x % req.y;}break;default:resp.code = -3; //代表请求方法异常break;}cout << "request: " << req.x << req.op << req.y << endl;// write(sock, &resp, sizeof(resp)); //这次就不能直接写入了,你得先序列化std::string send_string =SerializeResponse(resp); //序列化之后的字符串write(sock, send_string.c_str(), send_string.size());cout << "服务结束" << send_string << endl;}// 5.关闭连接close(sock);
}// ./CalServer port
int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for (;;) //创建线程完成,服务器就周而复始的运行,每来一个请求,它就创建线程,分离现场,然后进行业务处理{int sock = Sock::Accept(listen_sock);if (sock > 0){cout << "get a new client..." << endl;int *pram = new int(sock);pthread_t tid;pthread_create(&tid, nullptr, HandlerRequest, pram);}}return 0;
}CalClient.cc
#include "Protocol.hpp"
#include "Sock.hpp"void Usage(string proc)
{cout << "Usage: " << proc << " server_ip server_port " << endl;
}//./CalClient server_ip server_port
int main(int argc, char *argv[])
{if (argc != 3){Usage(argv[0]);exit(1);}int sock = Sock::Socket();Sock::Connect(sock, argv[1], atoi(argv[2]));//业务逻辑request_t req;memset(&req, 0, sizeof(req));cout << "Please Enter Date One# ";cin >> req.x;cout << "Please Enter Date Two# ";cin >> req.y;cout << "Please Enter operator# ";cin >> req.op;std::string json_string = SerializeRequest(req);ssize_t s = write(sock, json_string.c_str(), json_string.size());char buffer[1024];s = read(sock,buffer,sizeof(buffer)-1);if(s > 0){response_t resp;buffer[s] = 0;std::string str = buffer;DeserializeRequest(str,resp);cout << "code[0:success]: " << resp.code << endl;cout << "result: " << resp.result << endl;}// response_t resp;// s = read(sock, &resp, sizeof(resp));// if (s == sizeof(resp))// {// cout << "code[0:success]: " << resp.code << endl;// cout << "result: " << resp.result << endl;// }return 0;
}在客户端,我们输入了一下数据,然后把构建的请求序列化成字符串,然后就发字符串,发送字符串后,对端收到了,然后就响应,响应后我们就读,读的时候读到的一定是响应字符串,然后我们再对响应字符串进行反序列化,反序列化到response,然后就拿到了response的结果。对于server来讲,就是先进行读取,读取到的内容一定是序列化后的请求,然后我们先对请求进行反序列化,然后得到对应的结果并进行分析,分析完后得到响应,响应得到之后,再对响应进行序列化,然后把它写回去。所以我们就在代码中植入了序列化和反序列化的过程。
测试:
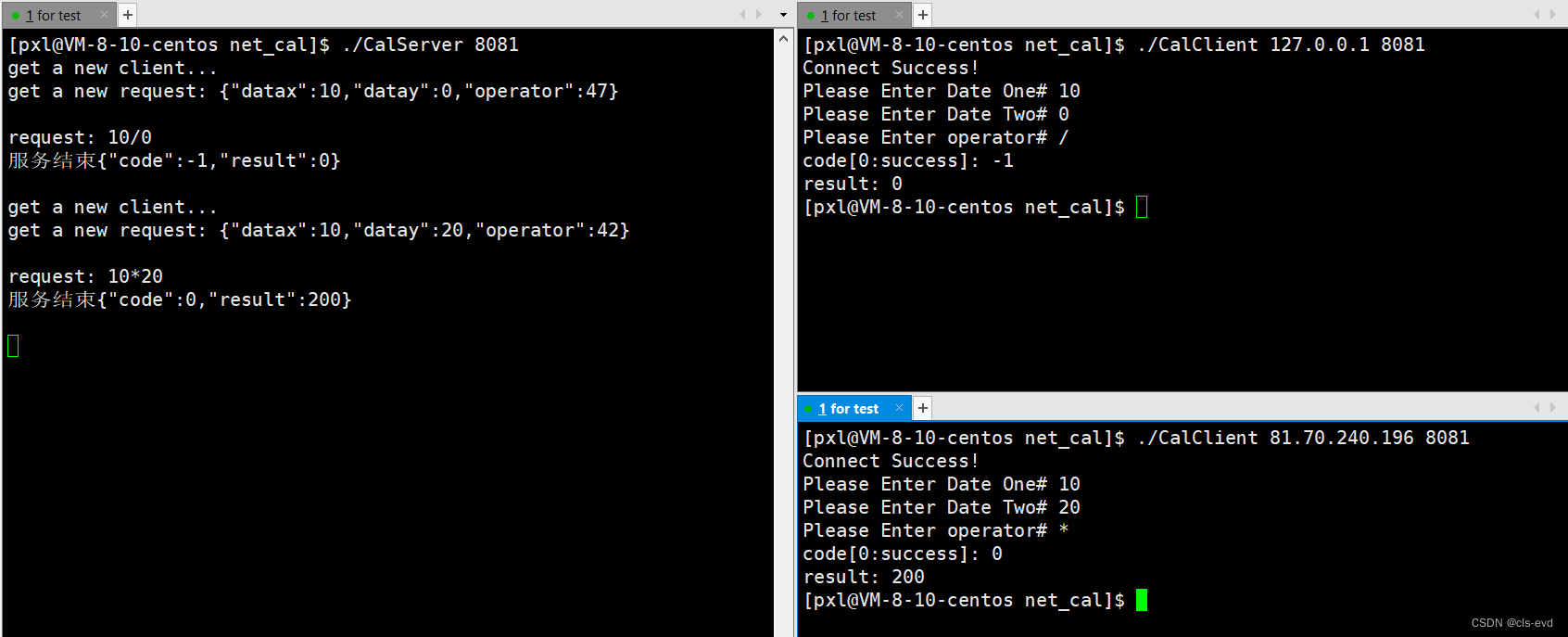
这就是序列化和反序列化,我们的最终目的是让网络程序在通信的时候,我们不想让他们直接传递结构化的数据,而是让他们进行互相发送字符串(方便我们后序做调整)。
对网络计算器的总结
我们刚刚写的cs模式的在线版本计算器本质就是一个应用层网络服务,我们的客户端用的是我们对应的linux的客服端,服务器是我们自己写的服务器。
我们所做的工作 :
1.基本通信代码是自己写的(一堆socket);
2.序列和反序列化是我们用组件完成的;
3.业务逻辑是我们自己定的;
4.请求,结果格式,code含义等约定是我们自己做的!
这就叫做我们完成了一个自定义的应用层网络服务。
结合上述,我们在看看OSI的七层协议
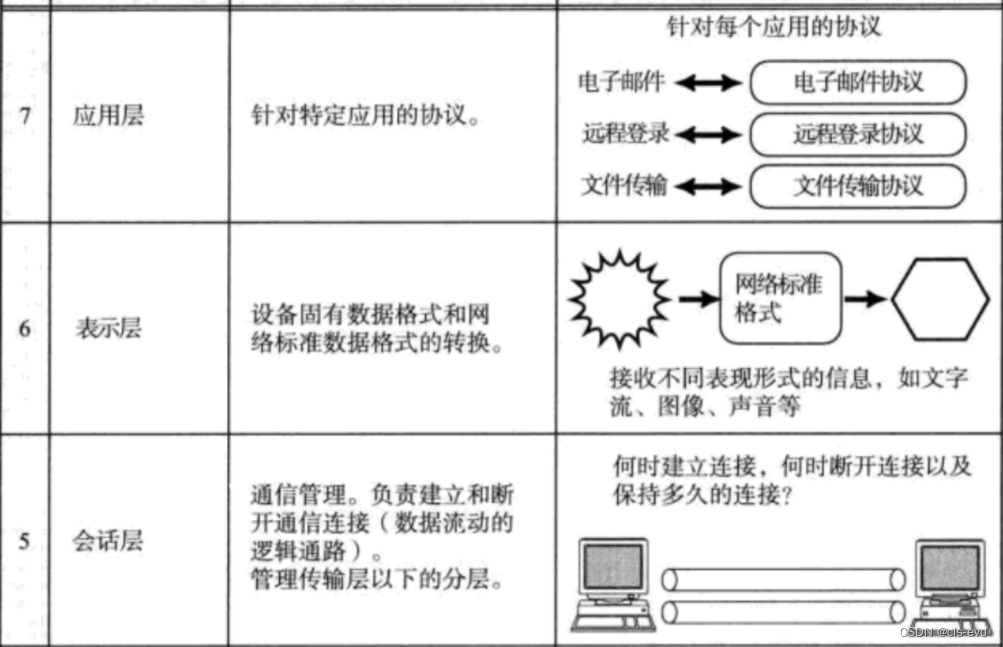
OSI和TCP/IP的差别无非就是上三层,TCP/IP上三层就叫做应用层。会话层就对应了我们做的工作1,让我们能进行正常的网络通信。表示层对应了工作2。应用层对应我们的工作3,4。OSI考虑的就是这个点,可是实际做下来后我们发现,这三层很多都是我们写的,甚至是用别人的组件写的。OSI制定的这三层是不可能完成独立开的,也不能写到内核当中,所以我们就把它三个在TCP/IP里放到应用层。说白了就是上层应用层我不写了你自己实现吧。所以就有了基本套接字,序列化和反序列化的基本组件,然后还有特定应用场景的各种协议的出现。
HTTP协议
虽然我们说, 应用层协议是我们程序猿自己定的.
但实际上, 已经有大佬们定义了一些现成的, 又非常好用的应用层协议, 供我们直接参考使用. HTTP(超文本传输协议) 就是其中之一.
http协议,本质上,在定位上和我们刚刚写的网络计算器,没有区别,都是应用层协议。
http的网络通信,序列化和反序列化,协议细节,都是http协议内部需要自己实现的。
认识URL
平时我们俗称的 "网址" 其实就是说的 URL.网址是定位网络资源的一种方式。
我们请求的图片,html,css,js,视频,音频,标签,文档,等这些我们都称之为资源。服务器后台使用linux做的。目前我们可以用ip+port唯一的确定一个进程。但是我们无法唯一的确认一个资源!公网IP地址是唯一确定一台主机的,而我们所谓的网络“资源”,都一定是存在与网络中的一台linux机器上!linux或者传统的操作系统,保存资源的方式,都是以文件的方式保存的。
eg:你今天刷的抖音,在抖音的服务器上一定是一个个的短视频,今天刷的视频,音频看的文档查看的网页全部是在linux当中以文件的方式存的。但linux系统,标识一个唯一资源的方式,我们通过路径进行!
所以,IP+linux路径就可以唯一的确定一个网络资源!!!
ip通常是以域名的方式呈现的。路径可以通过目录名+分隔符确认。
URL全称Uniform Resource Location,译为统一资源定位符。它就是通过网址确认哪一个资源在哪一个服务器上。
eg:
url字段解析
https:就是请求该资源的方法,说白了就是使用的协议 。
所以一个基本的URL构成就是通过协议,域名+资源路径可能还会带参,这样的方式去构成的URL。URL存在的意义叫做确认全网中唯一的一个资源。
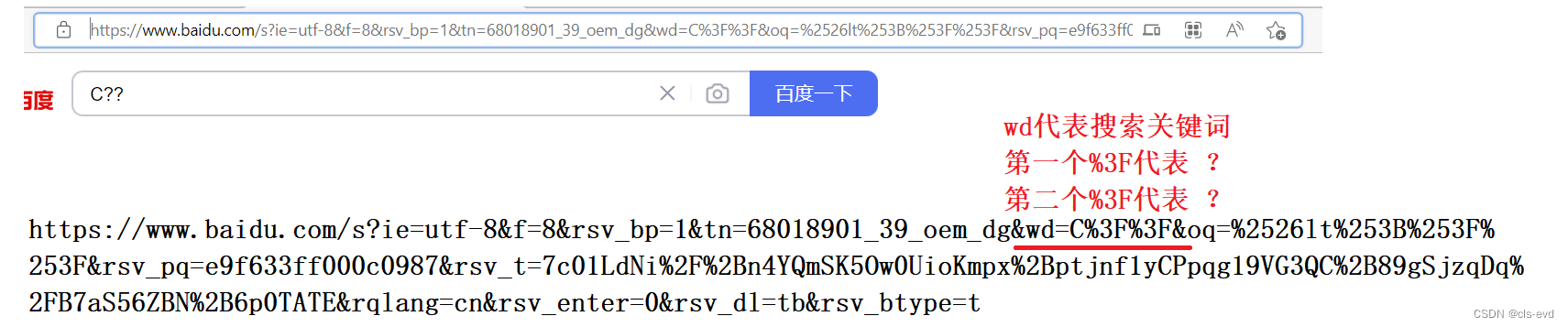
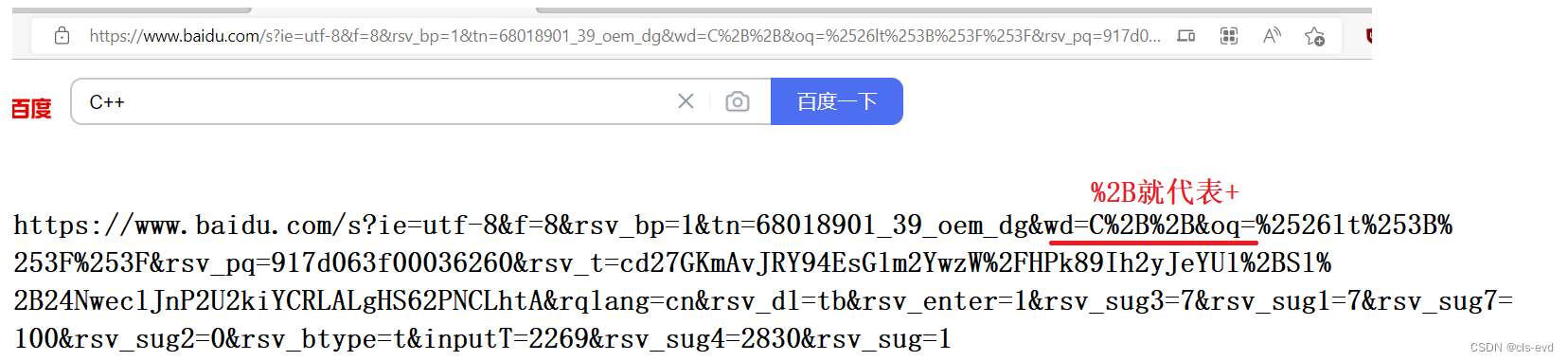
urlencode和urldecode
像 /, ?, : 等这样的字符, 已经被url当做特殊意义理解了. 因此这些字符不能随意出现.
比如, 某个参数中需要带有这些特殊字符, 就必须先对特殊字符进行转义.
eg:
说明我们在URL处理的时候,有些特殊符号是需要被特殊处理的,其中我们把像+,?这些在URL中不能直接出现的符号,由原始的字面值的样子,转化成这种16进制方案,我们称之为urlencode.叫做对字符进行转码。
将C??转化成C%3F%3F,这种样子,我们称之为encode(编码)。
将C%3F%3F转化成C??我们叫做decode(解码)。编码和解码是由浏览器自动帮我们编码,服务器收到之后可能要自己解码,但是我们一般不自己做。
这样处理的根本原因就是它其实不想让这些特殊字符在URL中出现,而影响URL本身的合理性。
转义的规则如下
将需要转码的字符转为16进制,然后从右到左,取4位(不足4位直接处理),每2位做一位,前面加上%,编码成%XY 格式
eg:
HTTP协议格式
简化对请求和响应的认识
无论是请求还是响应,基本上http都是按照行(\n)为单位进行构建请求或者响应的!
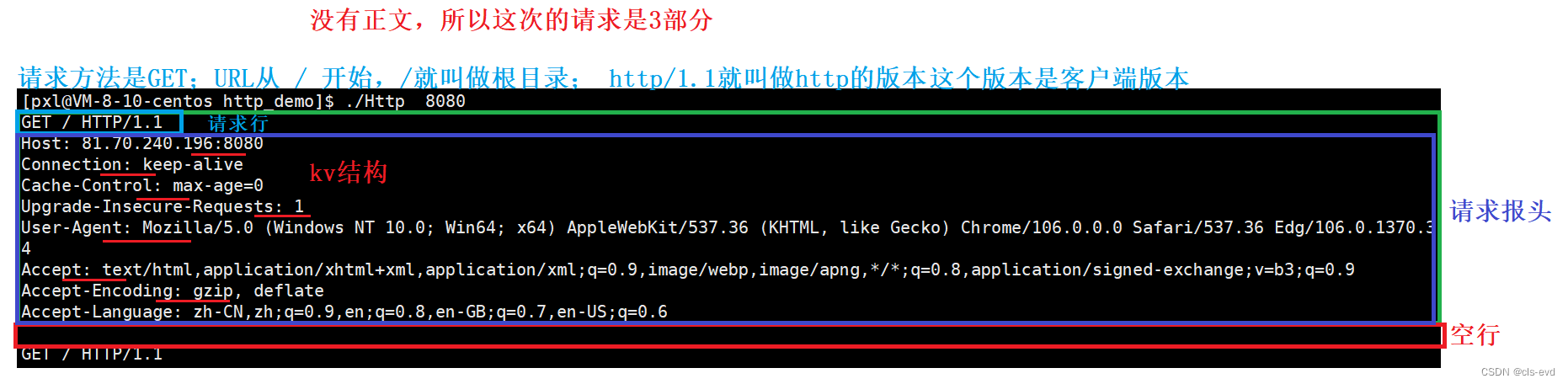
无论是请求还是响应,几乎都是由3或者4部分组成。
HTTP请求
http request的格式

http的请求的所有内容都是字符串(传视频,音频可能有二进制,但在它的报头里面我们不考虑)
请求行
请求行一般分为三部分:
请求方法;
URL(请求的资源定位服务);
http version(http协议的版本);
常见的方法比如get方法,URL一般是去掉域名之后的内容(也就是你要访问的网络的一个路径资源),http version也是一个字符串。
eg:http / 1.1。这三部分都已字符串的形式构成一个请求行,这个请求行中间以空格作为分隔符,分成三个区域,最后以\n结束。
请求报头
第二大块我们称之为请求抱头,这里画这么大仅仅是因为这里有多个请求抱头,实际上每个请求抱头依旧是以行为单位进行陈列的,构建成多行内容。每一行都是以key:value的方式呈现的。它的请求抱头是由一个一个的kv形式的属性构成。每一个属性的结束符都是\n。站在http服务器读取的时候,这部分全部是一行内容。
空行
第三部分是空行
请求正文
第四部分是请求正文(如果有的话)常见的请求正文主要是用户提交的数据。
如何理解普通用户的上网行为?
我们这个答案是简洁版本。仅仅分为两步
1.从目标服务器拿到你要的资源。
2.向目标服务器上传你的数据。
我们现在所有上网行为仅仅分为这两步。
eg:你平时刷抖音,抖音的视频可不是在你的手机上的,而是在服务器上,通过网络传的,所以那些资源是在服务器上的。你平时用的淘宝,京东,只要你是你看到的东西,基本是从服务器拿下来的。
比如我们进行登录,注册,支付,下单,再比如上传一个抖音,发朋友圈,这全部都叫做上传一个数据。
我们所有的上网行为无外乎这两种。这个行为对应到计算机当中就是IO的过程。而且人的所有上网行为本质都是进程间通信,进行间通信的过程(你给我发,我给你发,对我来讲就是IO)。
所有用户提交的数据,比如说是你要进行登录,注册...这样的信息,包括你上传的视频,音频都是在正文部分。
综上就是http的请求内容。
http的响应
http的响应的构成和请求在宏观上的构成是一毛一样的,它也是由三部分构成。
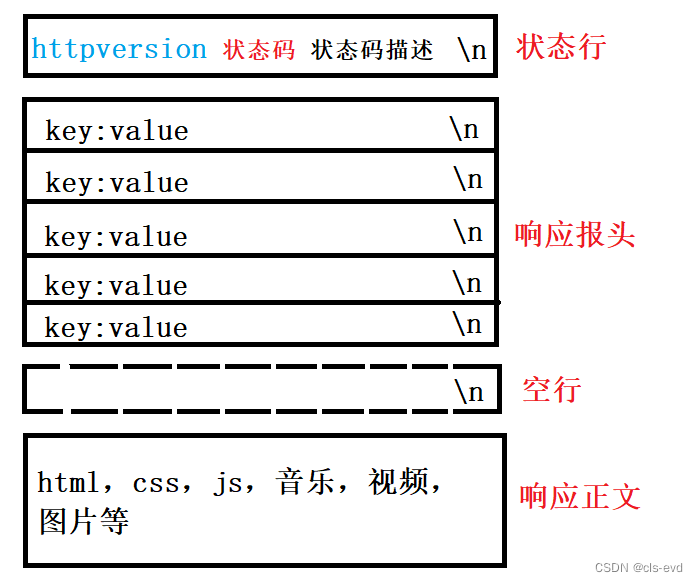
状态行
状态行也由三部分构成:
http version的版本;
状态码;
状态码描述;
http version比较常见的也是http/1.1 。状态码,最常见的一个就是404,404就是资源找不到,我怎么知道404是什么含义呢?所以404的状态码描述就叫做not found,表示你的资源找不到。
响应报头
同请求报头
空行
整行就是一个空行
响应正文
响应正文:比如你今天要进行数据请求的时候,你要进行登录,最后登录成功的时候,我要给你响应的时候,返回的肯定是登录成功之后我的网站的首页。所以这个响应里面经常是html,css,js,音乐,视频,图片等这些就叫做响应正文。
请求与响应的整体格式
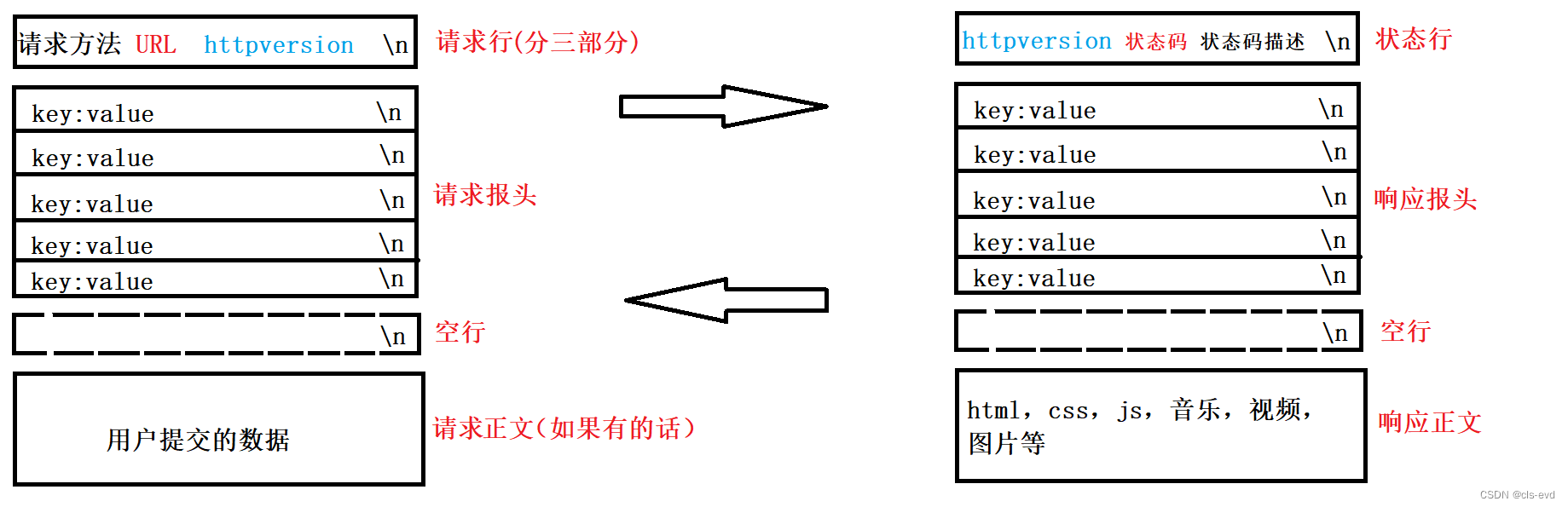
思考:无论请求还是响应最终所有的内容都是以行呈现的,http也是一个完整的协议。上面的两部分是服务器或者浏览器关心的,下面正文部分是人关心的。

我们需要讨论的问题
1.http如何解包,如何分用,如何封装?
2.http请求或者响应,是被如何读取的?
3.http请求是如何被发送的?
2,3结合就是一个问题,http request和http response 被如何看待?
http request和http response 被如何看待?
我们可以将请求和响应整体看做一个非常大的字符串!!!
 所以对于http来讲,但是http是由很多行构成的,看起来我们需要一行一行进行发送,但是实际上我们看他的时候就是一个长字符串,它只是文本格式是一行一行的。一旦它被看做一个大的字符串,那么它的读取和发送都是按照字符串进行读取和发送的。换句话说,越靠近头部的地方一定是越先被发送的,越靠近尾部的地方,越后被发送或者接受。
所以对于http来讲,但是http是由很多行构成的,看起来我们需要一行一行进行发送,但是实际上我们看他的时候就是一个长字符串,它只是文本格式是一行一行的。一旦它被看做一个大的字符串,那么它的读取和发送都是按照字符串进行读取和发送的。换句话说,越靠近头部的地方一定是越先被发送的,越靠近尾部的地方,越后被发送或者接受。
如何解包和封包呢?
在众多行中出现了一个空行,空行是一个特殊字符(空行什么都不写换一行,结束时\n再换一行),用空行可以做到将长字符串一切为二,这个大字符串以空格为分割符将它分为前半部分和后半部分。所以当我们解包一个http的时候,我们按行进行读,只要我们读到的一行内容是空行,我们就认为我把报头读完了,剩下的全部都是有效载荷。所以我们就能做到解包。封装的时候要构建http请求,请求行和报头全加上,最后再带上一个空行,然后在跟上正文,这就叫做封装。这就是http的请求,响应也同样如此。所以我们的http用来区分报头和有效载荷在编码层面上是通过一个特殊字符来区分报头和有效载荷的。
如何分用?
分用就是把你的有效载荷交给谁,这个问题不是http解决的,是具体的应用代码解决,http需要有接口来帮助上层获取参数。
http的请求和响应,在我看来是以行为单位罗列了一大批内容,在网络看来它就是一个大字符串,然后这个字符串左半部分和右半部分是通过空行分割的,所以我们能做到封装了,封装的时候就是报头+空行+正文,解析的时候一直读,只要读到空行,前半部分全都它的报头,后半部分就是正文。
HTTP操作
1.看看http请求
2.发送一个响应
http底层采用的依旧是tcp协议
http中面向字节流读的函数recv
这个函数是专门来进行网络读取所定制的一个函数。这个函数和read的使用几乎没有任何的差别,recv唯一多了一个flags,这个参数可以让我们以阻塞非阻塞包括读取后序的解密指针这样的一些东西,不过我们全程不设置或者默认为0.
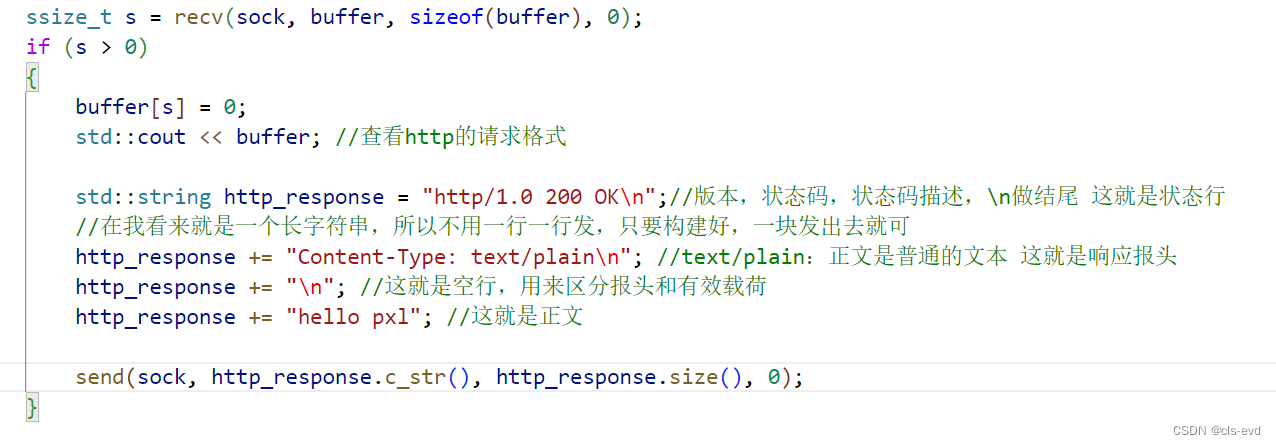
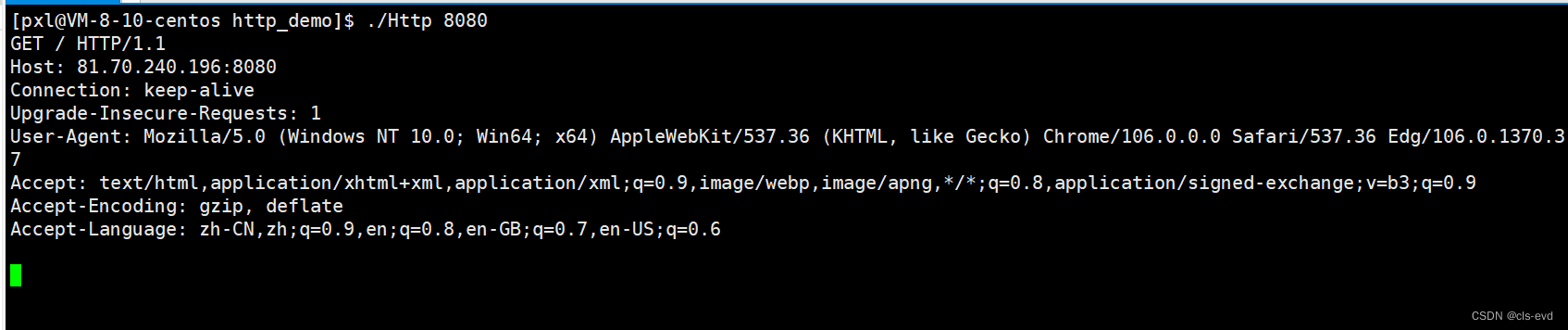
最简单的HTTP服务器
实现一个最简单的HTTP服务器, 目前我们的服务端啥也不干;
#include"Sock.hpp"
#include<pthread.h>
void Usage(std::string proc)
{std::cout << "Usage: " << proc << "port" << std::endl;
}void *HandlerHttpRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer << std::endl; //查看http的请求格式}close(sock);return nullptr;
}int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}}
}测试
我们运行是这个样子的
然后我们借助浏览器,在搜索栏输入服务器的ip+:+port
此时因为没响应,没给他发任何数据,但是此时我已近向服务器发送了多条http请求了
为什么客户端发了多条请求呢?
主要是因为http server得不到响应,所以它把自己请求在重复的发送。只要点击这个域名,就能把你的请求发送到我的云服务器上了。
HTTP请求
这就是一个较为完整的http请求
如果我们把换行符去掉,我们就能看到两个请求之间只空一行
这个http的请求和响应为什么都带了版本呢?
因为客户端是个软件,服务器也是个软件,两个都有版本。
eg:所有的软件都会升级,包括OS也会升级,现在有些人升级了微信,有些人没升级,作为服务器,是不会给新微信和就微信分别提供一个server提供服务的。而是根据你的微信的版本,如果你是老版本给你提供一些功能,如果你是新版本在给你提供一些功能。软件的版本决定它所能看到的功能,对于服务器来讲就可以统一使用一套服务来处理所有的新老客户端了。
对于HTTP请求的报头字段的解释
- Host:代表这个请求你想访问谁,后面跟着的就是我的公网ip和port。
- Connection:代表的是连接类型,我们都是基于短链接的
- Cache-Control:代表双方通信时的一些缓存信息
- Upgrade-Insecure-Requests:代表协议升级情况
- User-Agent:代表我们的浏览器访问时客户端的信息,比如平时我们下载软件的时候
User-Agent详解
它有很多的OS,默认给我们选中的就是windows,这就是因为你的http请求里就包括了User-Agent,里面就写了你的客户端信息。
博主用手机进行访问
我们可以看出 User-Agent显示的就是博主手机的信息。
所以我们用不同的设备去访问网站的时候,浏览器会自动根据你的本地平台帮你去识别你的主机,客户端是什么,然后服务端收到这些请求之后它可以识别这些信息,尤其是下载平台,它会根据你的设备给你推测出你的设备所适合下载的软件。
- Accept-Encoding:代表接受的编码类型
- Accept-Language: 代表接受的语言类型
服务器构建响应
现在我们的程序已经见到这个请求了,接下来我们想在服务端构建一个响应。
我们现在的响应就是无论请求什么,我都返回hello这样的字符串内容。返回时候就是向客户端写入,写入我们可以采用write。但是这里我们推荐send,这个是在linux中特有的,针对于tcp设计的接口。
send
除了多了一个参数,其他的和write一毛一样。
这样就可以直接进行发送响应吗,答案是不可以,因为我们是在模拟http的行为,你要写的可是一个http的响应,一个响应由三部分构成,我们不能只把响应正文给它,状态行,报头,空行我们都要带上。
当我们读这个http的响应或者请求时,是从上往下读的,也就是一行一行的去获取的,其中Content-Type属于响应报头的属性之一,所以我是如何知道你的有效载荷是什么类型呢?Content代表内容,Type代表类型。Content-Type就代表的是我的请求或者响应如果携带了正文,那么正文的类型是什么,就叫做Content-Type。
Sock.hpp
#pragma once#include<iostream>
#include<string>
#include<cstring>
#include<cstdlib>
#include<sys/socket.h>
#include<netinet/in.h>
#include<arpa/inet.h>
#include<unistd.h>using namespace std;
class Sock
{
public:static int Socket(){int sock = socket(AF_INET, SOCK_STREAM, 0);if (sock < 0){cerr << "socket error" << endl;exit(2); //直接终止进程}return sock;}static void Bind(int sock,uint16_t port){struct sockaddr_in local;local.sin_family = AF_INET;local.sin_port = htons(port);local.sin_addr.s_addr = INADDR_ANY;if (bind(sock, (struct sockaddr *)&local, sizeof(local)) < 0){cerr<<"bind error!"<<endl;exit(3);}}static void Listen(int sock){if (listen(sock, 5) < 0){cerr << "listen error !" << endl;exit(4);}}static int Accept(int sock){struct sockaddr_in peer; //对端的信息socklen_t len = sizeof(peer);int fd = accept(sock, (struct sockaddr *)&peer, &len);if (fd >= 0){return fd;}return -1;}static void Connect(int sock, std::string ip, uint16_t port){struct sockaddr_in server;memset(&server, 0, sizeof(server));server.sin_family = AF_INET;server.sin_port = htons(port);server.sin_addr.s_addr = inet_addr(ip.c_str());if (connect(sock, (struct sockaddr*)&server, sizeof(server)) == 0){cout << "Connect Success!" << endl;}else{cout << "Connect Failed!" << endl;exit(5);}}
};HTTP.cc
#include"Sock.hpp"
#include<pthread.h>
void Usage(std::string proc)
{std::cout << "Usage: " << proc << "port" << std::endl;
}void *HandlerHttpRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));// 这种读法是不正确的,只不过现在没有被暴露出来罢了ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer; //查看http的请求格式std::string http_response = "http/1.0 200 OK\n";//版本,状态码,状态码描述,\n做结尾 这就是状态行//在我看来就是一个长字符串,所以不用一行一行发,只要构建好,一块发出去就可http_response += "Content-Type: text/plain\n"; //text/plain:正文是普通的文本 这就是响应报头http_response += "\n"; //这就是空行,用来区分报头和有效载荷http_response += "Shi Jiayi is a beautiful and hard-working girl"; //这就是正文send(sock, http_response.c_str(), http_response.size(), 0);}close(sock);return nullptr;
}int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}}
}测试

我们就在浏览器上看到了刚刚写的hello pxl.这就叫做http的响应。这就叫做http的简单响应和简单请求。
HTTP的请求与响应总结
http的请求就是请求行,请求报头,空行,请求正文;
响应就是状态行,响应报头,空行,响应正文 。
对我们来讲就是3~4部分,中间用空行作为区分,我们就能很快的区分清楚他们之间的一个格式要求。实际上在编码层面上,你发过来的请求都是被我读到buffer里面,从前向后读。虽然你的请求和响应是行状的格式,但是在我看来就是一个大字符串,所以我就可以在读取的时候对我们的协议内容做读取分析。所以http协议,如果自己写的话,本质是,我们要根据协议内容进行文本分析!(因为协议别人已经给我们定好了)得到对应的响应,然后将响应构成字符串,在响应回别人。
观察百度的网页
我们登录一下百度的服务器.没有telent命令我们可以手动安装一下
sudo yum install telnet telnet-server
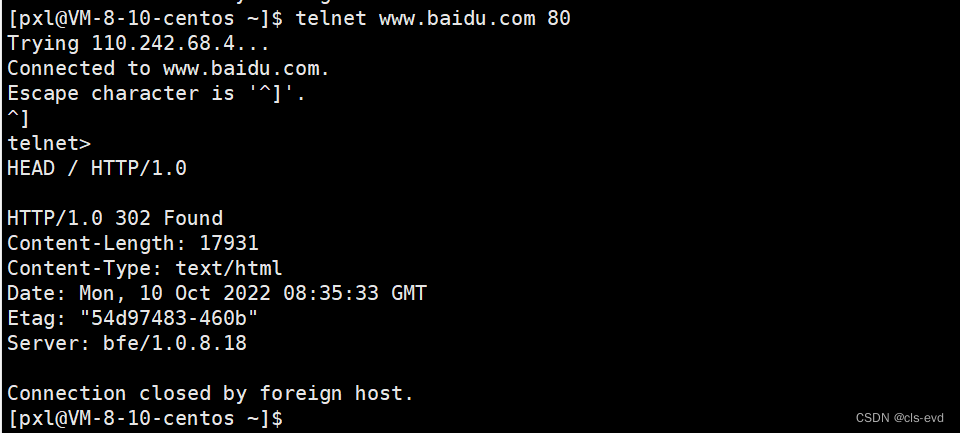
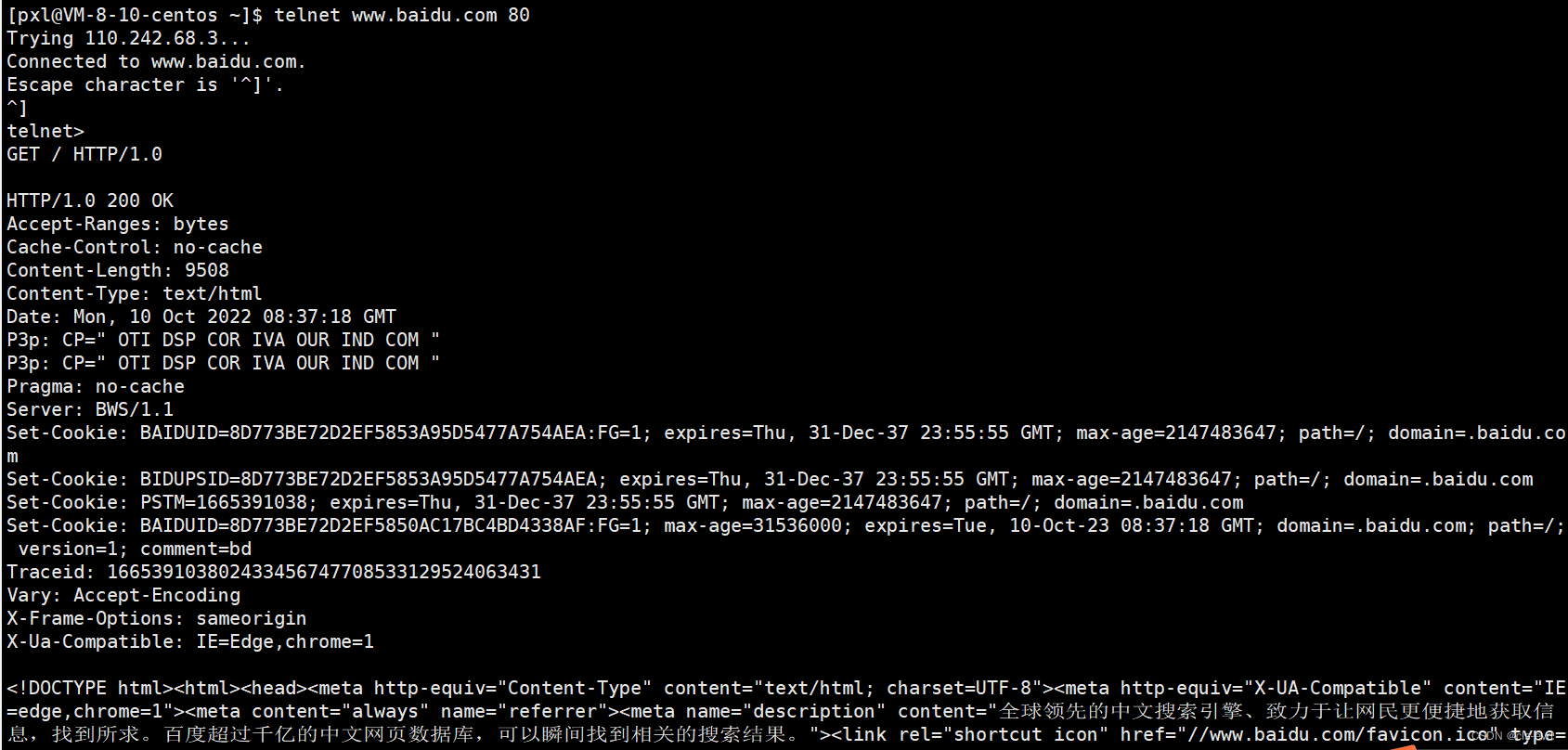
手动的用Telnet构建一个请求
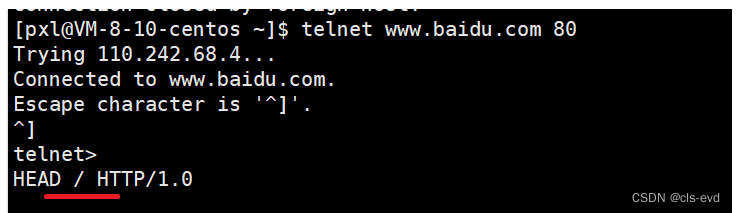
1.telnet www.baidu.com 80
2.Telnet窗口中按下“Ctrl+]”;
3.先按下回车,输入
GET / HTTP/1.0
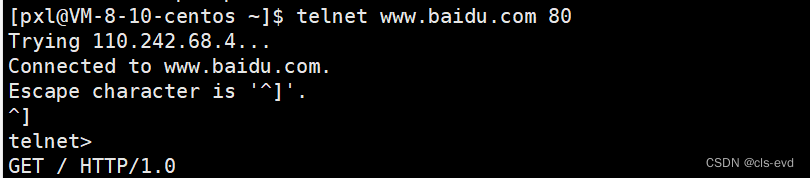
此时就得到了百度对应的响应
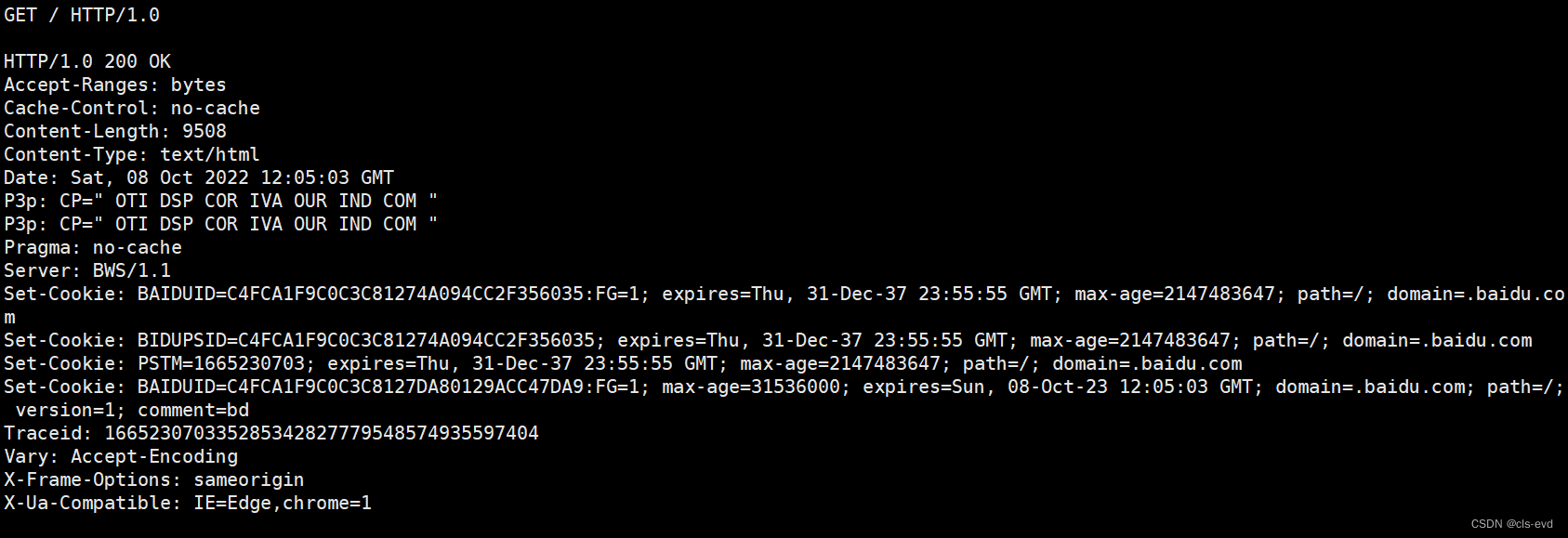 百度的http版本是1.0,状态码是200,状态描述是OK(这是百度的老的服务器)紧接着就是百度一堆的响应报头,包括了Content-Type,时间,Server等。紧接着就是传说之中的网页
百度的http版本是1.0,状态码是200,状态描述是OK(这是百度的老的服务器)紧接着就是百度一堆的响应报头,包括了Content-Type,时间,Server等。紧接着就是传说之中的网页

这些就是给我们压缩之后的一些html网页,它里面内置了很多html,js的内容。
我们在浏览器(Edge)打开百度官网 ,然后进入开发人员工具
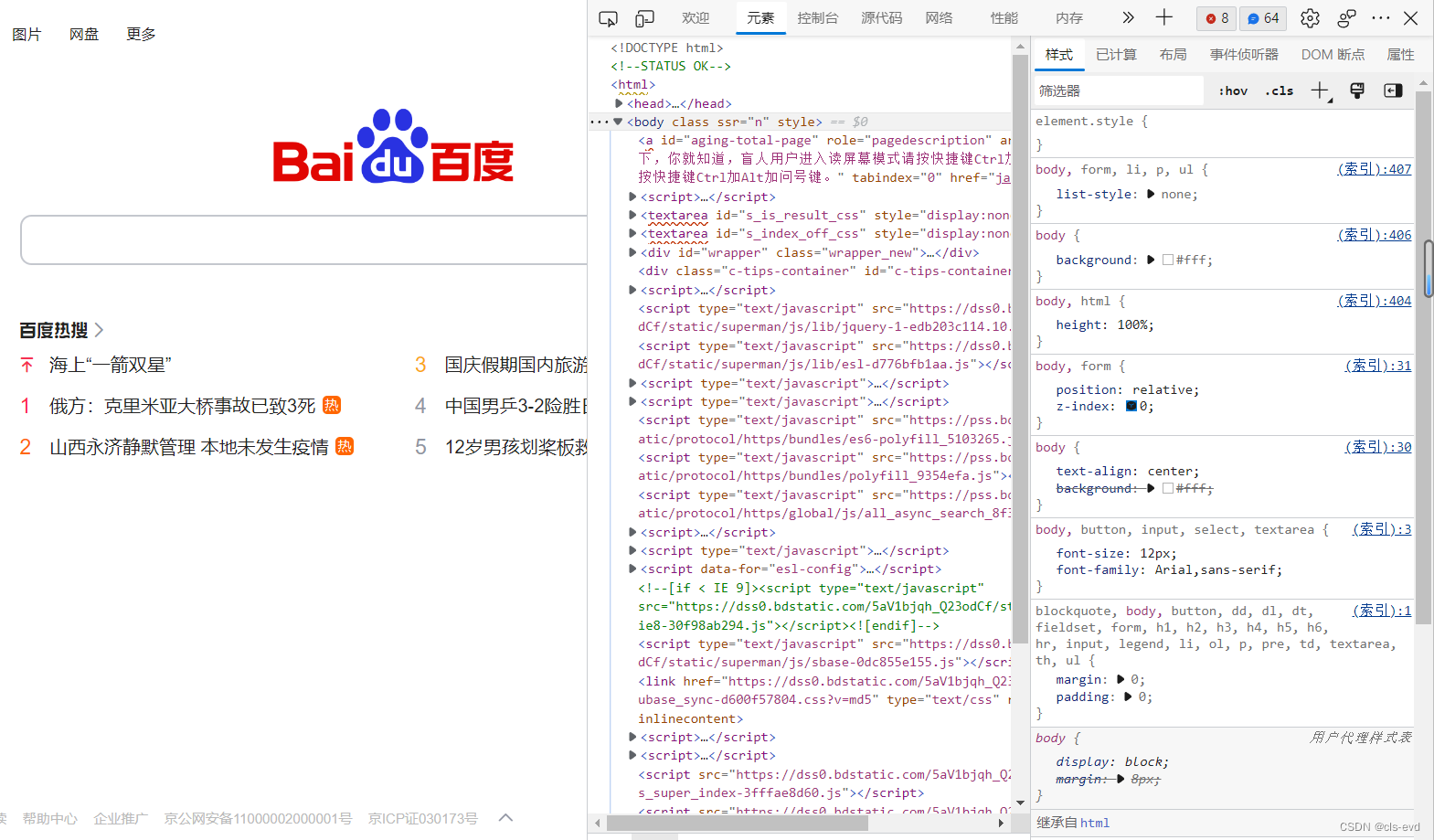
这个元素里面就是百度的网页内容对应我们linux的那一大段内容(linux是为了效率,减少成本,把\n,空行全部去掉了,所以看起来乱) 。
总结一下:我们实际上在http请求时,它响应的正文部分一般都是我们的网页内容。包括图片视频这些。所以才有了http响应标识的这部分。
再谈http请求的细节
http请求没有使用json或者没有直接使用json,那么它的整个报头或者正文用空行作为分隔符,然后整体以行为单位,这种也算一个序列化,这种和发送结构体不一样,http本身所有的文本行都是按行陈列的,那么其中写入的时候一行一行去写,读取再一行一行去读,本质上就是一种序列化和反序列化的过程,只不过没有显示化的把他显示出来。http里有很多的方法,包括很多的属性。
HTTP请求
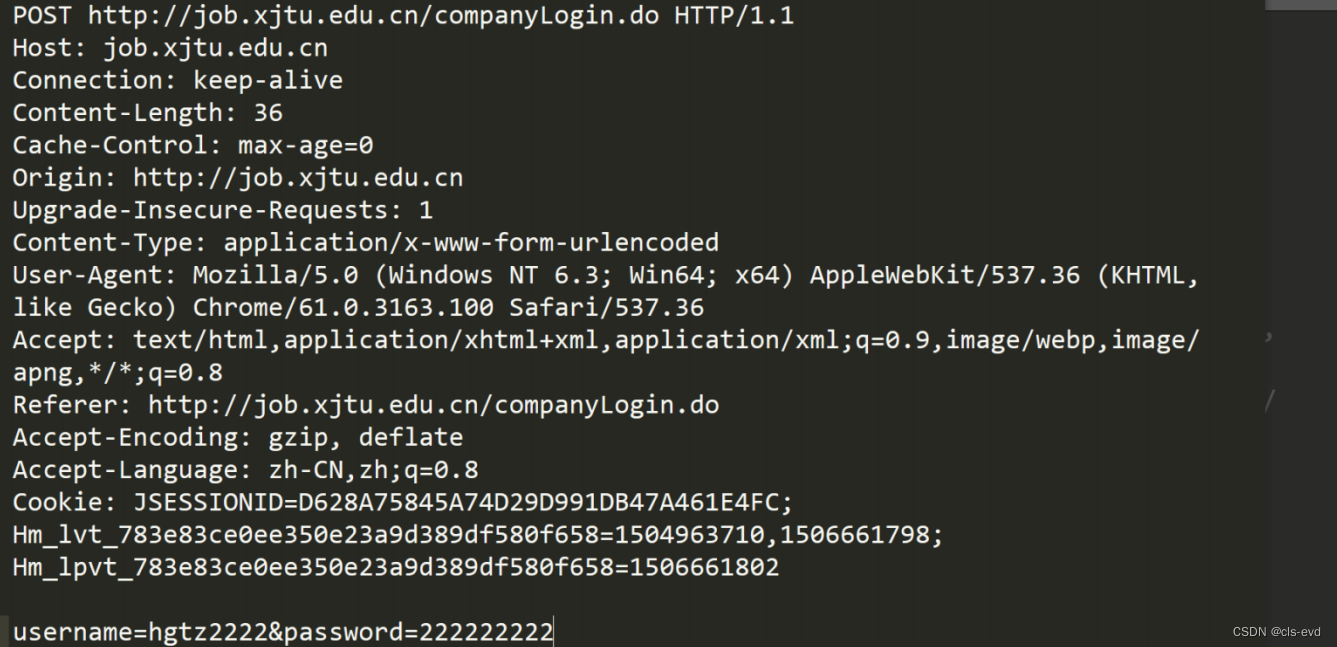
- 首行: [方法] + [url] + [版本] 像如图这种的URL,有时候服务器要做一个代理服务器要拿去你要访问资源的全的URL,大多数的URL还是像之前一样去掉域名的那种。
- Header: 请求的属性, 冒号分割的键值对;每组属性之间使用\n分隔;遇到空行表示Header部分结束。
- Body: 就是http请求或者响应的正文;空行后面的内容都是Body. Body允许为空字符串. 如果Body存在, 则在Header中会有一个Content-Length属性来标识Body的长度。
理解Content-Length
实际上我们代码在读取http请求的时候,这种recv的读法是不对的,只不过现在没有被暴露出来

http的请求是通过多行的方式呈现的,每一行用\n作为分隔符。我们今天考虑的是server端进行读取,当我们读取的时候,一次是定义了一个大的缓冲区。当你在recv的时候,这个请求一定在底层,http的底层就是tcp,当你在进行recv时,无论是从网络里读,还是从tcp里读,一定是tcp协议给你的数据,那么其中你在recv的时候,你定义的是1024*10个字节。
实际上:
1.当http发来请求的时候实际上并不是像你所想一样,一个一个发送的,有可能http客户端会以某种方式向我们发送多个请求。
2.你今天的缓冲区定义的是1024*10这个大小,如果它是多个请求的话,每个请求是1024的大小,你一次就把所有请求一起读完了。如果缓冲区大小是1025这个大小,那么除了把整个报文读完,还把下一个报文多读了一个字节。
读取要求
第一:我们要保证每次读取都是读取完整的一个http请求。
第二:保证每次读取都不要将下一个http请求的一部分读到(我在读取的时候客户端有可能发送来多个http请求,我可能在读取的时候,一个http请求读完了,因为我缓冲区设置的问题,而导致它把下一个报文多读了,这个时候下面的报文是残缺的报文,上面的报文也不正确因为多了一块数据,这次就需要你自己去对他做分析,处理,这样是比较麻烦的,而且容易出问题)。
你怎么保证你每次读到的是一个完整的http呢?
当我们读取一个完整的http请求的时候,我们按行读取,如何判定我们将报头部分(包括请求行和请求报头)读完了呢?
读到空行,我们就可以确定报头全部读完了。
报头读完了就看后面还有没有正文,如果有正文,如何保证把正文全部读取完成呢?而且不要把下一个http的部分数据读到呢?
你要决定报头后面有没有正文,本质上是决定一个请求或者是一个响应,它对应的有没有涵盖它的请求或者响应的数据。报头后面有没有正文这个和请求方法有关。
假设有正文的话,你如何知道空行之后有多少个字符呢?
我不知道,但是当我读到正文的时候,我很清楚我已近把报头读完了,报头读完了,我们就能正确提取报头中的各种属性,其中包括一个字段,Content-Length。如果后面还有正文的话,那么报头部分有一个属性:这个属性就是Content-Length,它表明正文部分有多少个字节!!!
虽然没有学tcp,但是我们知道,所有的数据都是通过fd读取的!所以我无脑读,一直读到空行,我就能保证把http协议报头部分全部读上来,其中就包括了Content-Length,Content-Length就表明了如果有正文的话,正文部分的字节数。所以当我们正常读取的时候,一旦读到空行,然后我们再来看它的Content-Length,根据Content-Length确定读取多少个len自己的正文。Content-Length的存在就允许我们一字不差的吧它的正文部分全部读取到。
换句话说,报头读取的时候以空行为分隔符,把报头先得到,然后根据报头中的Content-Length在读取正文,这个正文我们就称之为http协议的有效载荷,Content-Length表明,http协议如果携带有效载荷,它的 有效载荷是多长。Content-Length也叫自描述字段。
如何读到一个完整的http协议?
1.有了空行,我们可以保证把报头全部读完
2.报头全部读完,我们就能分析方法和分析Content-Length,从而得出要不要读正文以及正文多长
3.正文是多少字节,我们按照Content-Length把正文全部读上来,
至此,我们就能读到一个完整的http请求或者响应。
- Content-Length:帮助我们读取到完整的http请求或者响应。同时根据空行能做到将报头和有效载荷进行分离(分离的过程就是解包的过程)。当你没有正文的时候,报头属性里面是不存在Content-Length属性的。这就是规定。
HTTP响应
- 首行: [版本号] + [状态码] + [状态码解释]
- Header: 请求的属性, 冒号分割的键值对;每组属性之间使用\n分隔;遇到空行表示Header部分结束
- Body: 空行后面的内容都是Body. Body允许为空字符串. 如果Body存在, 则在Header中会有一个Content-Length属性来标识Body的长度; 如果服务器返回了一个html页面, 那么html页面内容就是在body中.
同样的如果没有写Content-Length,浏览器也会正常显示,就比如我们自己实现的服务器发送的响应,这个就和浏览器的编写,应用层的支持是否严格有很大的关系,其实应用层实际上做了很多的约定,但是应用层要与人进行打交道,所以你曾经定好的再好的规则,只要是人参与进来了,它的支持度并不好,相当于我做了规定,但是有人就是不遵守,而且这个人还不少,那么不遵守只能让浏览器厂商针对这种情况做一些优化,但是一旦设计到内核,大家基本上都会遵守的。
HTTP的请求方法
http请求是包括请求的方法,URL和http的版本。http的版本最早的是1.0版本,使用最广泛的是1.1版,现在最新的还有2.0版。http 1.0和1.1最主要的区别是是否支持长连接。
短链接
短链接:一个请求,一个响应,close socket。客户端发起一个请求,服务器给一个响应,服务器响应完毕后把链接一关。我们刚刚缩写的就是短链接。http协议最早使用的就是短链接。一个请求,一般就是请求一个资源,比如一个请求就是请求一张网页,一个图片,一个视频,一个音频。请求完资源后链接关闭。
早期的http1.0为什么用短链接呢?
1.当时的网络资源并不丰富,主要以文本,最多是图片为主。
2.当时的服务器压力并不大,请求的资源都比较短小。网速比较好,服务器上的资源就比较大,网速特别差,服务器上的资源就比较小。eg:1,2G的时代我们能看文字,3G的时代我们能看图片,4G的时代我们可以看视频。资源变的越来越丰富,本质就是每一个资源的体积变的越来越大了。
最主要是因为短链接简单。
HTTP的方法
无论是请求还是响应都会携带http的版本。分别代表客户端和服务器采用的http版本。
http方法中,GET和POST方法是最重要的两个方法,没有之一。
GET大部分都是获取资源;
POST是传输资源;但其实他俩都可以进行获取和传输。
- PUT方法:你在浏览器上访问某些资源的时候,你一点击就自动给你下载了,实际上那个下载就对应的是PUT方法。
- HEAD方法:其实就是客户端告诉服务器,我不要正文,只要报头。
eg:
HEAD方法就只拿到了http的报头,没有正文。
用GET方法就拿到了报头和正文。
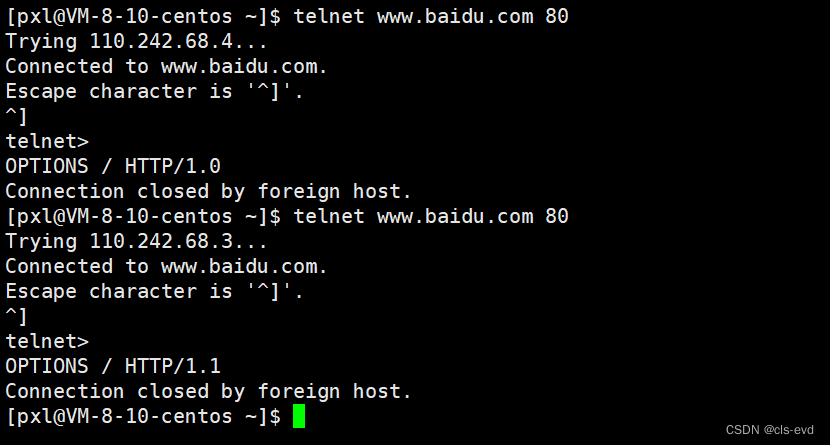
实际上HTTP看起来服务很多,但是对于一个web服务器来说,很多方法都是默认关掉的,
eg:OPTIONS,HTTP 1.1虽然支持,但有可能用协议的人把这个方法给禁掉了。
像PUT,DELETE,OPTIONS,TRACE,CONNECT这些方法http协议是支持的,但实际上不一定被使用协议的人所打开。别人就把这些方法禁止掉了,不让你用,一般的http协议,最多给你提供的方法就是GET,POST,HEAD。其他的不给你暴露出来。主要是为了防止出现一下恶意用户,比如你把PUT暴露出来了,有些恶意分子,不断像你的服务器上传数据,最后把你的磁盘打满,还有一些直接通过DELETE方法删除你的数据。这肯定是不行的,所以我们只给你暴露出有限的方法。
/ (根目录)
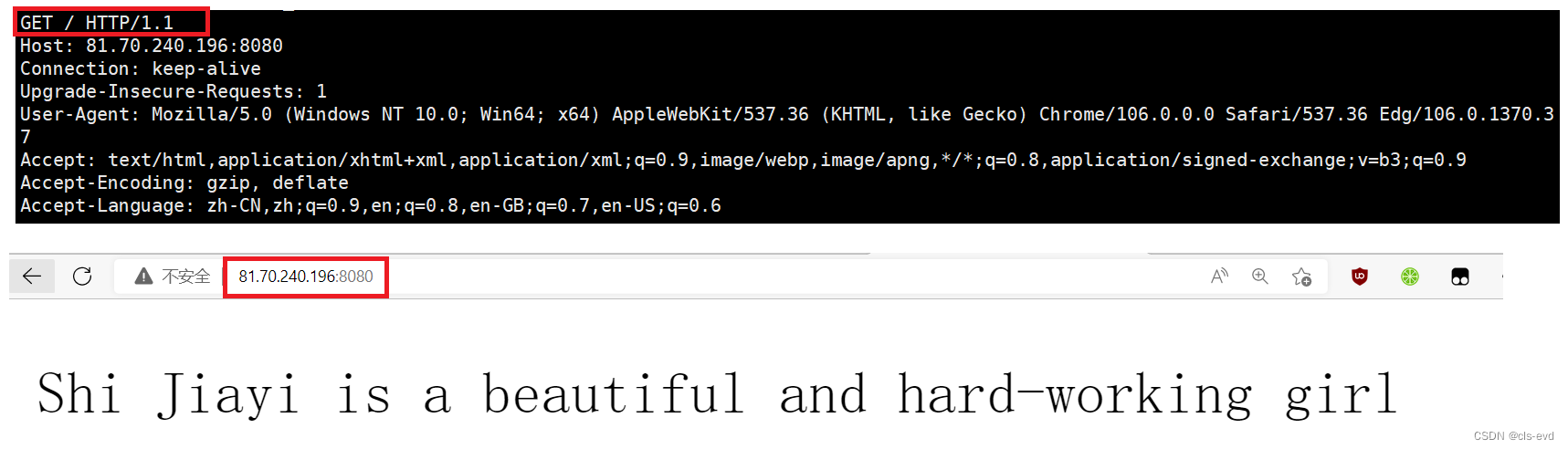
首先我们在做请求的时候,永远会带一个 / ,这个 / 叫做要请求的资源。
当我请求时,请求的就是这里的 / ,服务器是怎么看待这个 / 的,linux中这个 / 代表了根目录。但是在http请求中 / 并不是根目录,而叫做web根目录。
eg:我们再次运行我们的服务器:
如果请求默认是8080(8080后面啥也不带),我们看到对应的请求就是一个 /
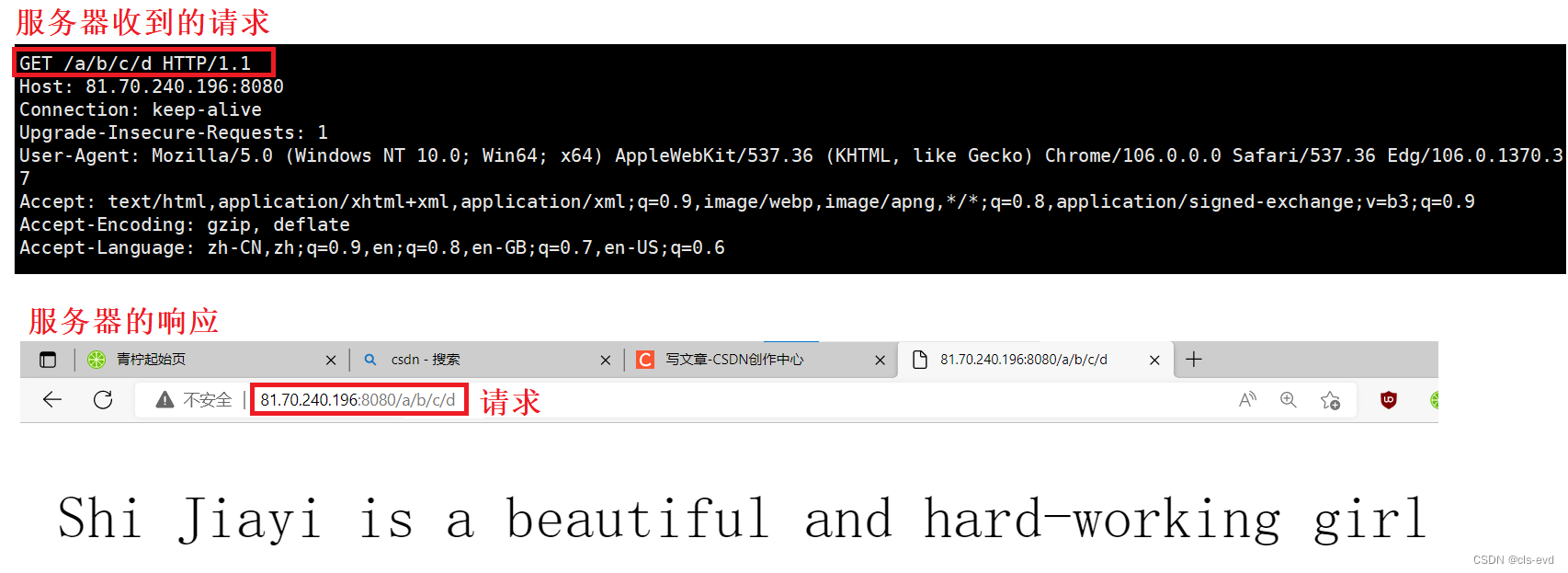
如果你后面带了对应访问服务器上的某个路径(/a/b/c/d),其中就会把路径显示到这里。
所以这个 / 就叫做我们要访问的资源所在的路径, 我们一般要请求的一定是一个具体的资源
比如:你要请求的是一个网页,图片。你给我一个 / ,意思就是说我要请求的是web根目录下的所有内容,我把这个网站的所有内容全部发给你。但是这样肯定是不行的,我们要具体指明网页或图片的路径。
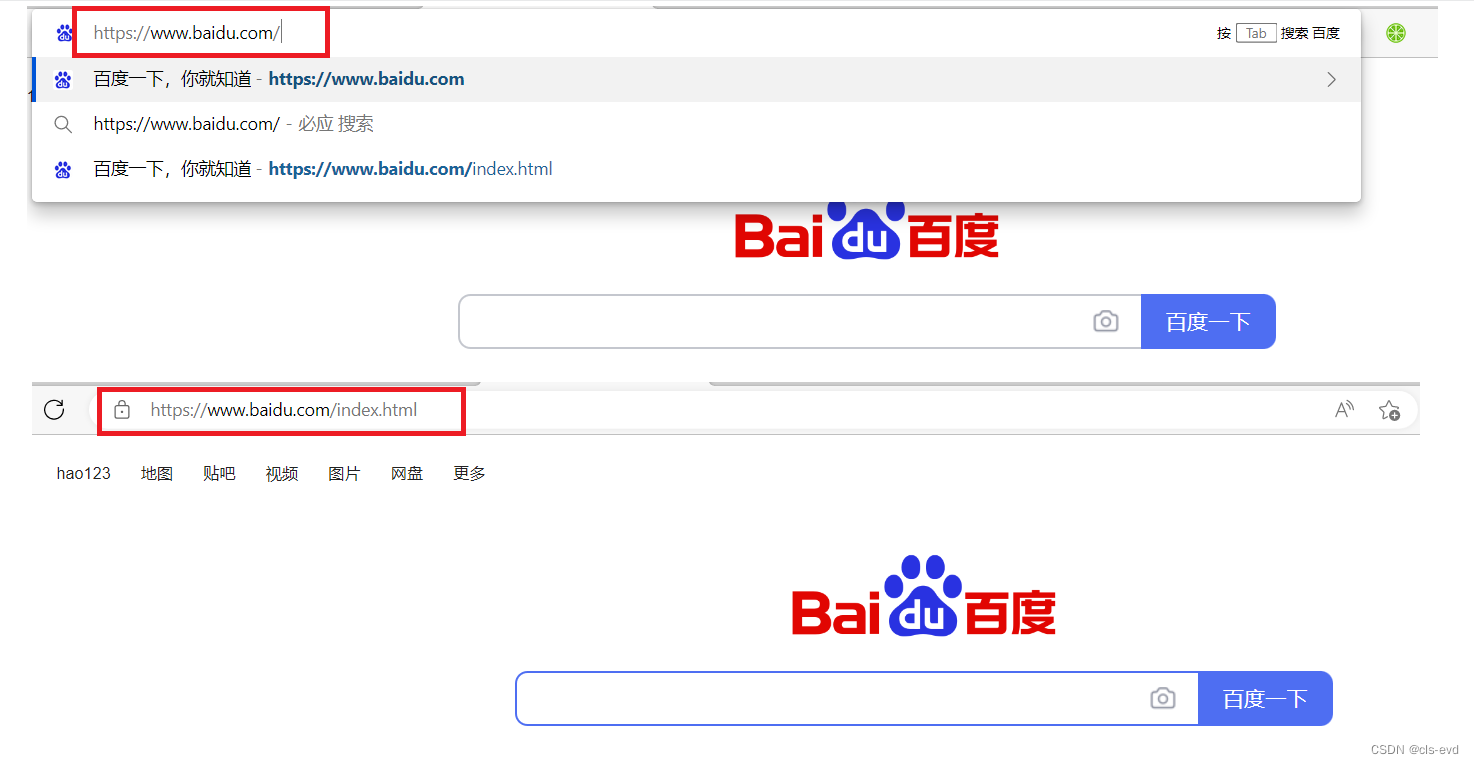
但是如果请求是 / ,意味着我们要请求该网站的首页!!!,首页一般叫做index.html ,或者是index.htm 。换句话说你是 / 这么请求的,别人的服务器可能最终默认的会把它的首页信息给你返回。
eg:我访问百度,两种访问的方式都能拿到百度的首页
实际上当你请求时,如果你的请求时 / ,我们的服务器它不会把web根目录下所有的内容给你返回,而是想办法给你把根目录下的首页返回,一般所有的网站,都要有默认的首页信息,对应的就是index.html这样的内容。
总结:当我们请求某个资源的时候,我可以通过带一个完整路径的方式,也可以直接请求 / ,默认就是首页。
实验
依然是基于我们上面的服务器代码
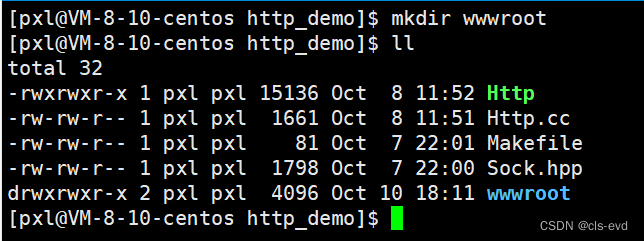
首先在当前路径下建立一个wwwroot目录,这个wwwroot我们就称之为http的web根目录
在该目录下我们新建一个index.html 就是http它的一个首页信息。
这个http请求就是当用户在请求时通过http协议来把我们所对应的当前目录下的web根目录下的网页信息给你返回。
响应报头部分
首先,我们指明访问文件的路径。此时别人给我请求时,我就可以把这个网页信息返回。

但是返回的时候,不仅仅返回正文网页信息,而是还要包括http的请求
Content-Type 代表正文部分的数据类型,今天我们响应回去的不是字符串,而是把web服务器的根目录的index.html响应回去。

ps:Content-Type 对照表
HTTP Content-type 对照表 (oschina.net)

接下来我们还可以带一个Content-Length,代表这个文件的大小。
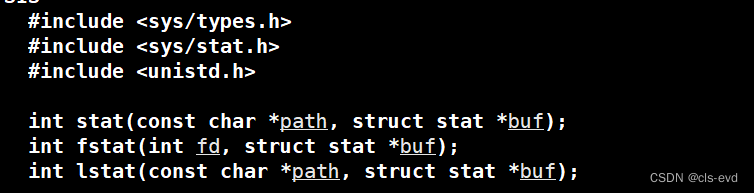
stat
我们今天用stat获取文件大小。
stat可以通过指定的文件路径,获取文件的指定属性 。-1就是失败,0是成功。这个stat的结构体是一个输出型参数,我们要把所有的属性获取出去。
st_szie就代表了文件的大小。
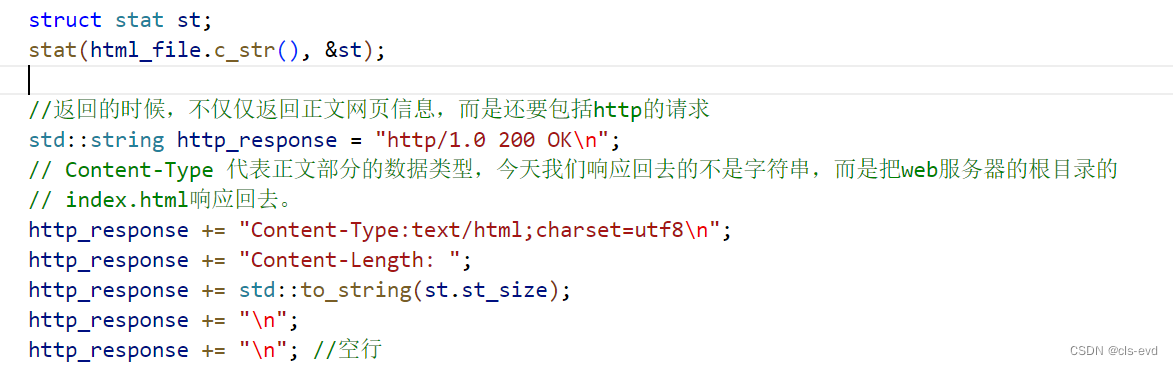
响应正文
接下来就是正文,上面的步骤就叫做构建一个响应.
这次的正文就是要拿的这个网页内容。
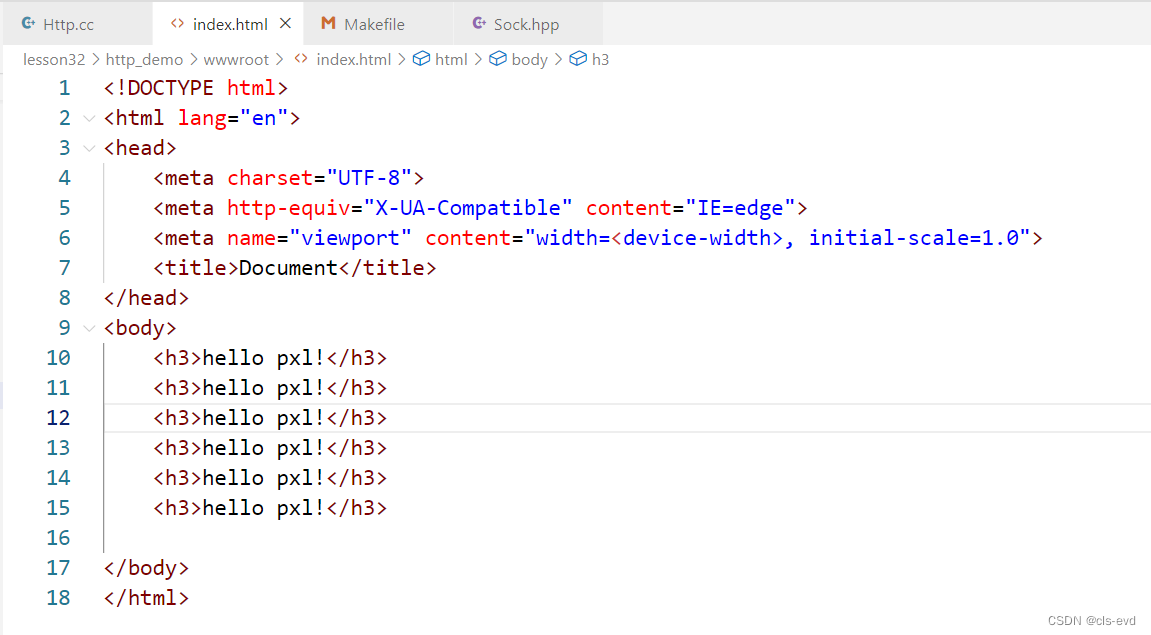
完整代码
Http.cc
#include"Sock.hpp"
#include<pthread.h>
#include<sys/types.h>
#include<sys/stat.h>
#include<unistd.h>
#include<fstream>#define WWWROOT "./wwwroot/"
#define HOME_PAGE "index.html"// 其中wwwroot就叫做web根目录,wwwroot目录下放置的内容,都叫做资源!
// wwwroot目录下的index.html就叫做网站的首页
void Usage(std::string proc)
{std::cout << "Usage: " << proc << "port" << std::endl;
}void *HandlerHttpRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));// 这种读法是不正确的,只不过现在没有被暴露出来罢了ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer; //查看http的请求格式// std::string http_response = "http/1.0 200 OK\n";//版本,状态码,状态码描述,\n做结尾 这就是状态行// //在我看来就是一个长字符串,所以不用一行一行发,只要构建好,一块发出去就可// http_response += "Content-Type: text/plain\n"; //text/plain:正文是普通的文本 这就是响应报头// http_response += "\n"; //这就是空行,用来区分报头和有效载荷// http_response += "Shi Jiayi is a beautiful and hard-working girl"; //这就是正文// send(sock, http_response.c_str(), http_response.size(), 0);std::string html_file = WWWROOT; //访问的文件在这个路径下html_file += HOME_PAGE;struct stat st;stat(html_file.c_str(), &st);//返回的时候,不仅仅返回正文网页信息,而是还要包括http的请求std::string http_response = "http/1.0 200 OK\n";// Content-Type 代表正文部分的数据类型,今天我们响应回去的不是字符串,而是把web服务器的根目录的// index.html响应回去。http_response += "Content-Type:text/html;charset=utf8\n";http_response += "Content-Length: ";http_response += std::to_string(st.st_size);http_response += "\n";http_response += "\n"; //空行//接下来才是正文std::ifstream in(html_file);if(!in.is_open()){std::cerr << "open html error!" << std::endl;}else{std::string content; //正文内容std::string line; while(std::getline(in,line)) //按行读取 {content += line; //正文就全部在content里面了。}http_response += content;in.close();send(sock, http_response.c_str(), http_response.size(), 0); //响应回去}}close(sock);return nullptr;
}int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}}
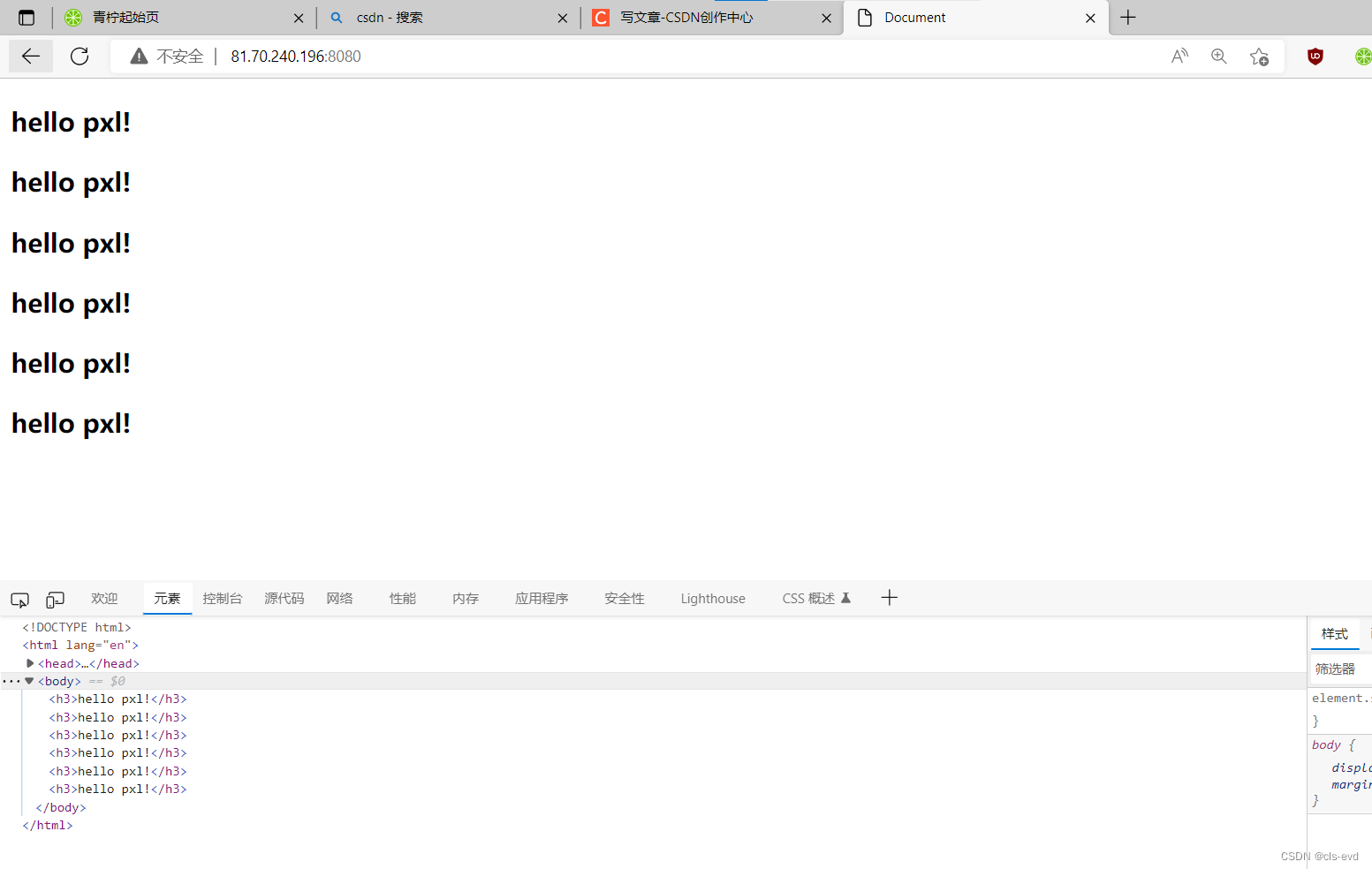
}测试:
ps:对于port,0-1023是系统内置的端口号,我们用不了,1024之后的随便用
比如我们将网页内容调整一下(服务器不用关闭,直接修改)
此时我们就看到了修改后对应的网页内容
其中wwwroot就叫做web根目录,wwwroot目录下放置的内容,都叫做资源!换句话说我将来可以在这个wwwroot下定义一个图片目录,网页目录,视屏目录...最后你要访问什么资源就是从这个wwwroot开始,来去访问你想访问的资源的。
eg:我们在访问网站的时候,上面是有对应的路径资,/ 这个一定是它的服务器上的web根目录,后面的就是具体路径
web根目录可以拷贝到linux下的任何目录下。wwwroot目录下的index.html就叫做网站的首页
当一个用户发起请求的时候,如果它的请求是根目录,服务器内部会对你的方法做判断,你访问的是 / ,就直接把你的路径改成web服务器下的首页信息。
验证GET和POST方法
上面我们做的事情就是就是把http的响应由字符串转换成了文件,实际上将来要访问很多资源,就是在web根目录下有很多的资源,让你去访问。
我们平时有注册或者登录的经历(输入账号和密码),就需要有一个输入框,你所看到的输入框实际上就是网页。
推荐学习前端网站:w3school 在线教程https://www.w3school.com.cn/
GET方法
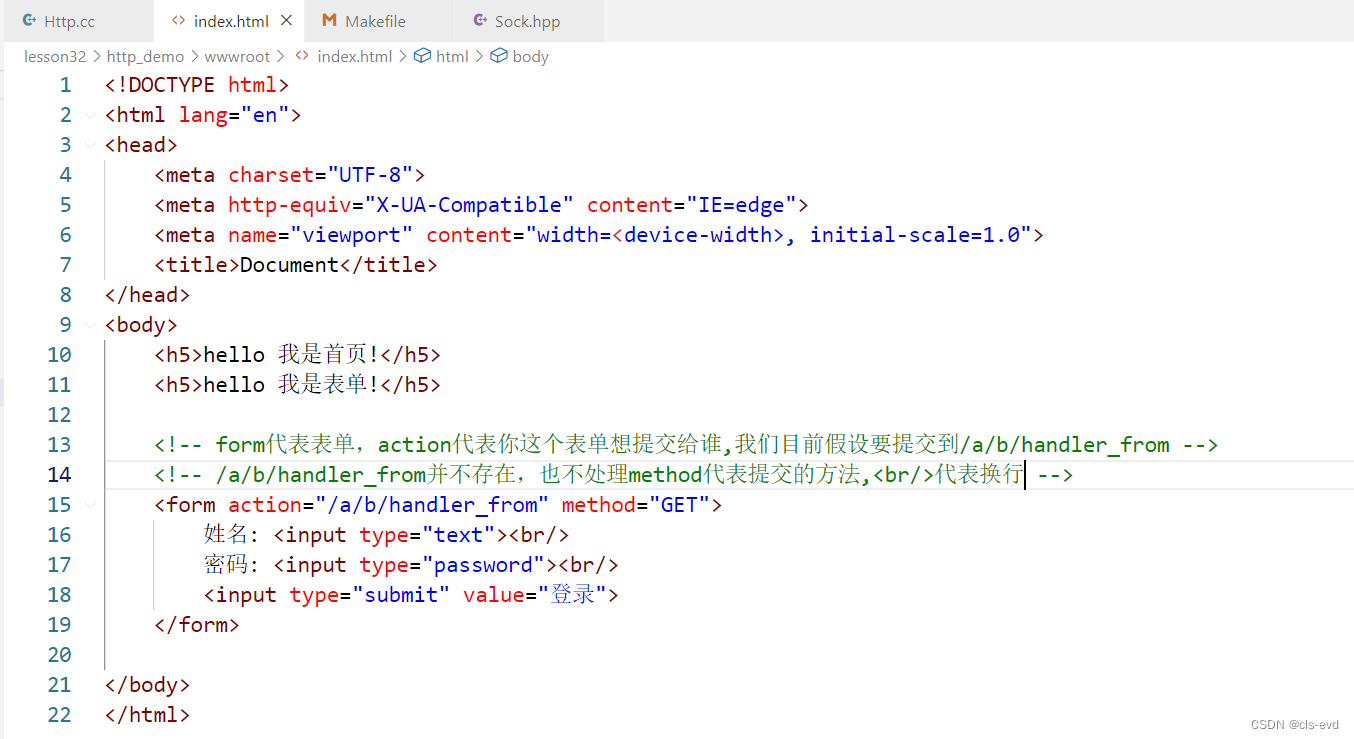
html的表单
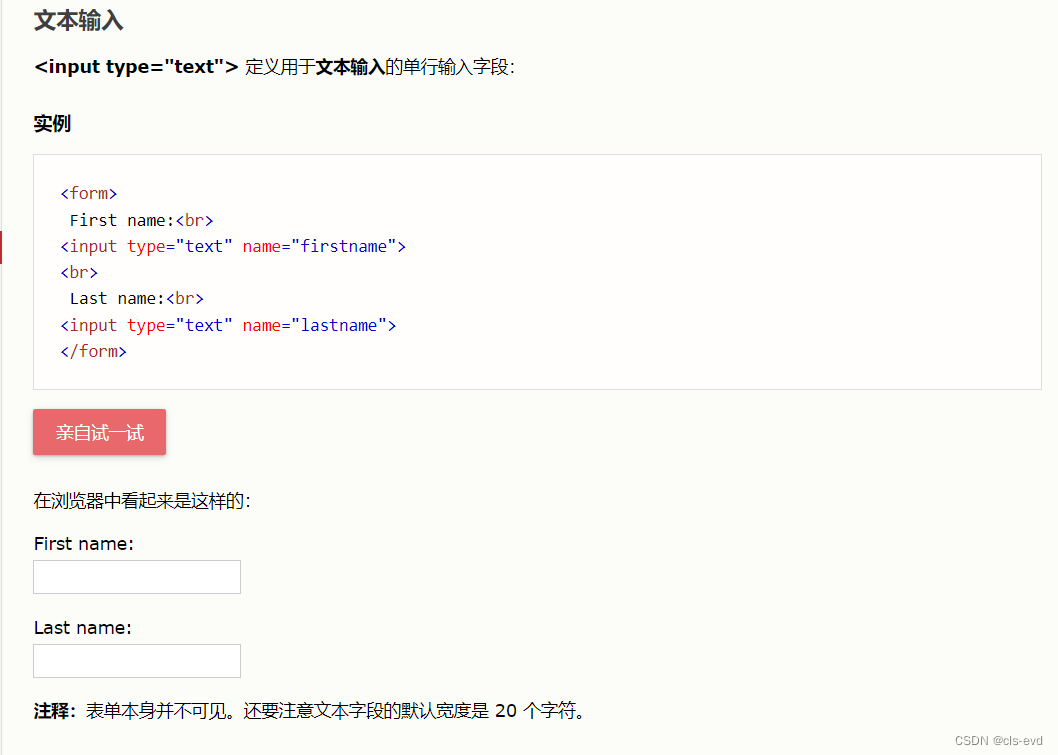
制作表单
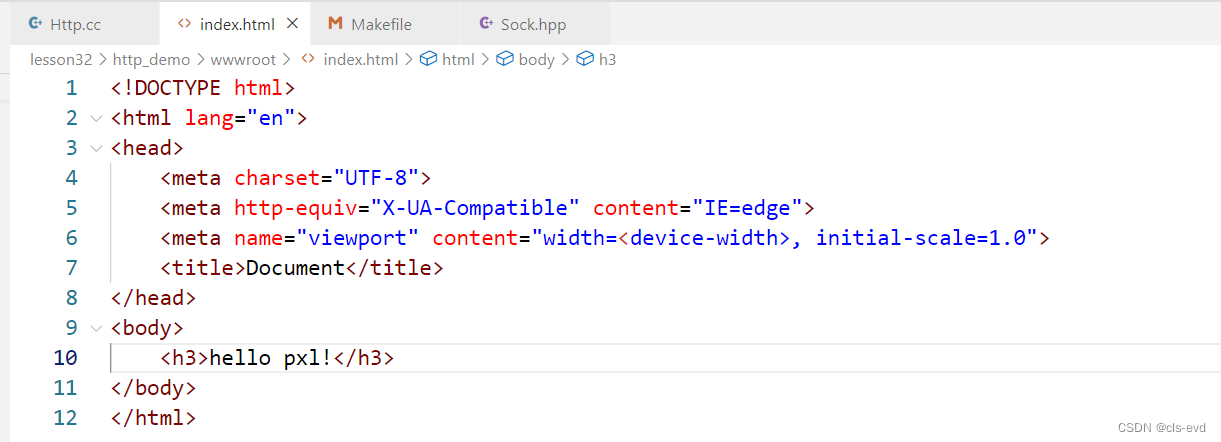
我们将我们的index.html首页进行修改
结果:
我们在增加一个登录选项
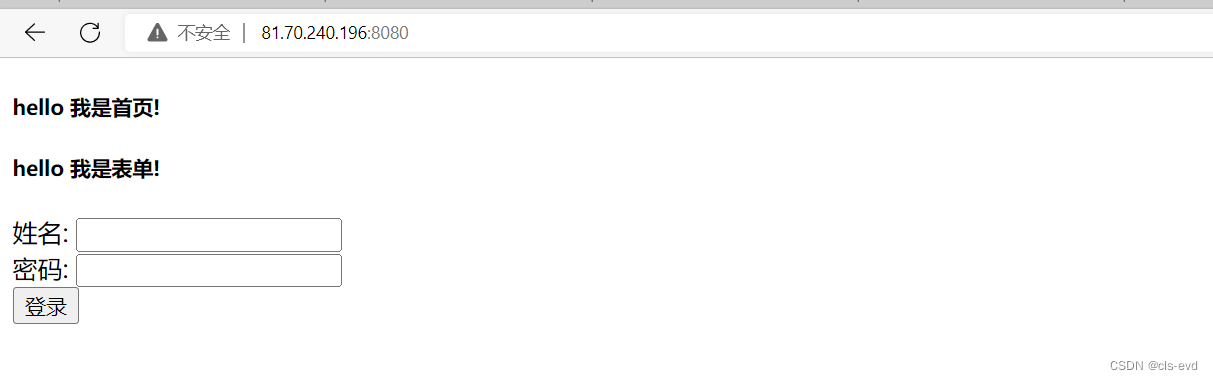
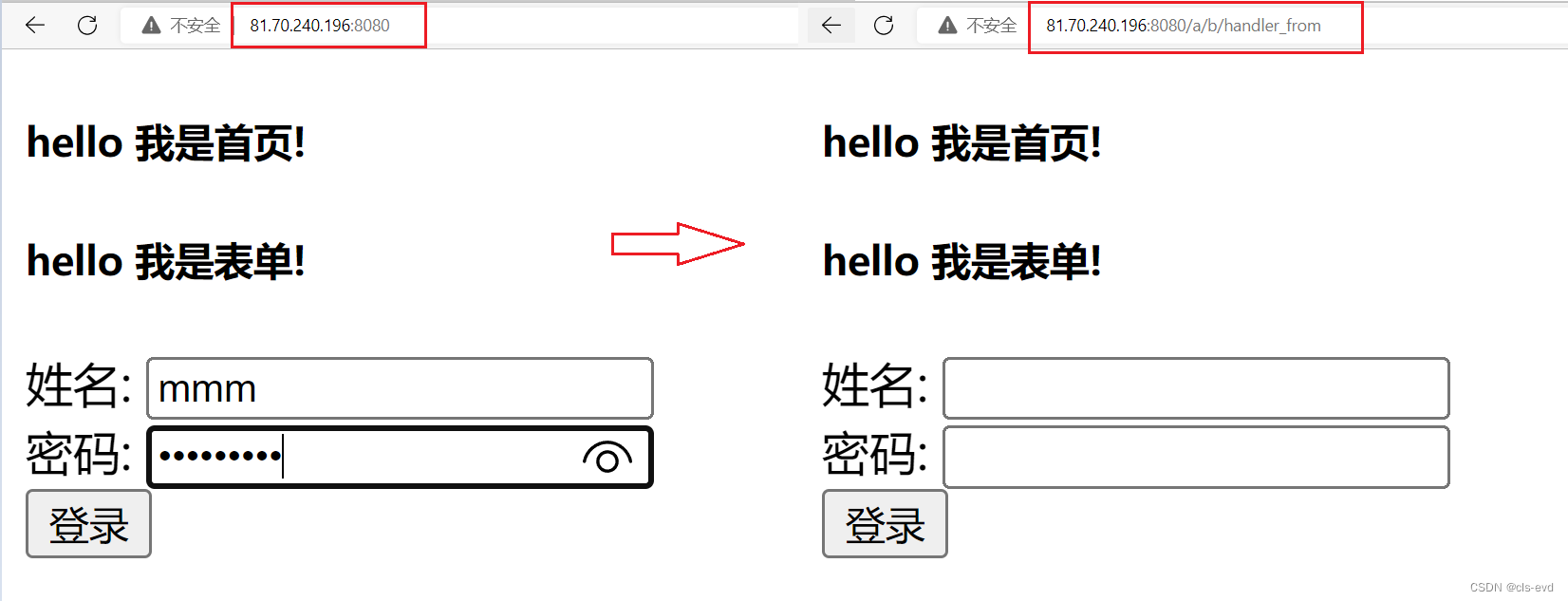
我们发现输入信息点击登录以后?后面没有任何内容,这是因为表单中这两个输入框,我们没有给他起名字,所以就无法获取参数
ps:URL 通过?来带参数,连接域名和参数,经常会用到
再次修改
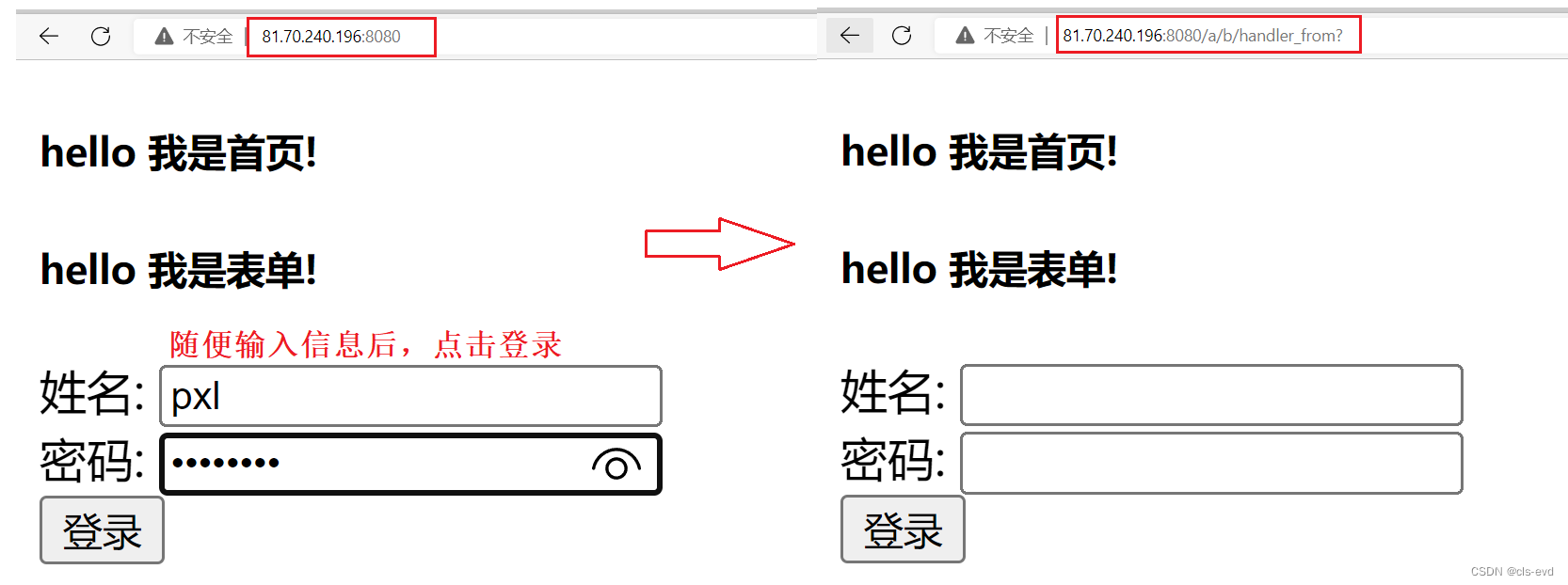
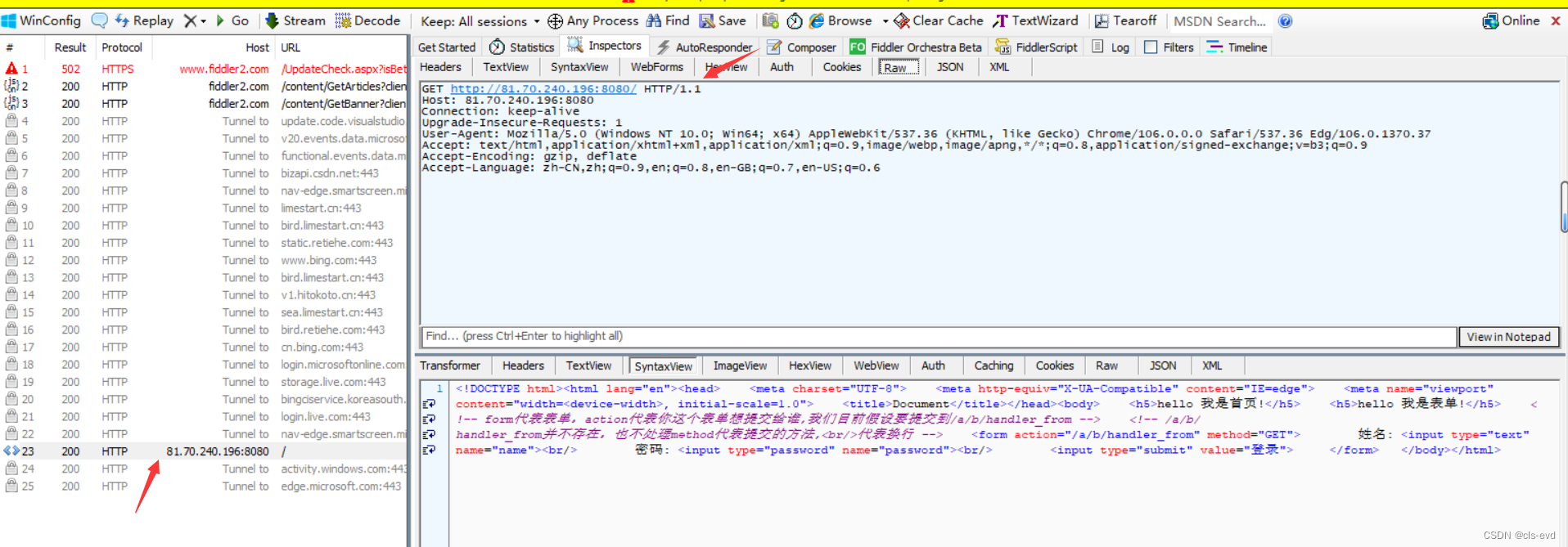
我们这里用的是GET方法,当我们传入参数,密码,一点击登录提交,它就会直接访问 /a/b/handler_from?name=pxl&password=123456。
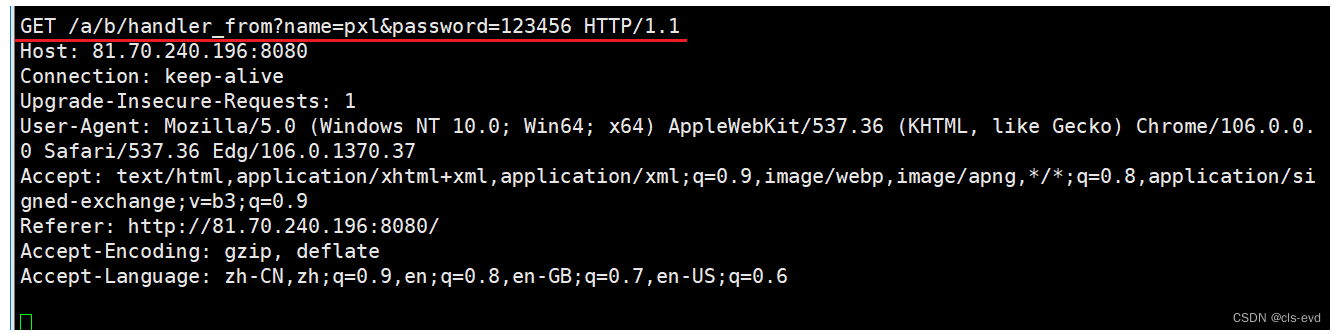
服务器的http请求
我们用的是GET方法,我们没有正文,提交的这两个参数是拼接在URL后面的以?作为分隔符,两个参数用&进行隔离 。
GET方法,如果提交参数,是通过URL进行提交的。
换句话说,实际上在服务器中,当我们输入表单提交,用的是GET方法的时候,提交参数的时候,浏览器自动把你的表单里的信息姓名和密码拼接在URL的后面,然后让你的http请求拿到这样的数据,这样的话,前端的数据就被后端的C++代码拿到了,我们实际上拿到的这个请求,参数是在我们读到的这个请求当中的,所以数据就被C++程序拿到了,C++程序拿到后就可以做字符串分割,提取出用户名和密码,再继续用C++在服务器后端做一些连接数据库,访问数据库,和你输入上来的用户名,密码作对比,从而让你实现登录过程。
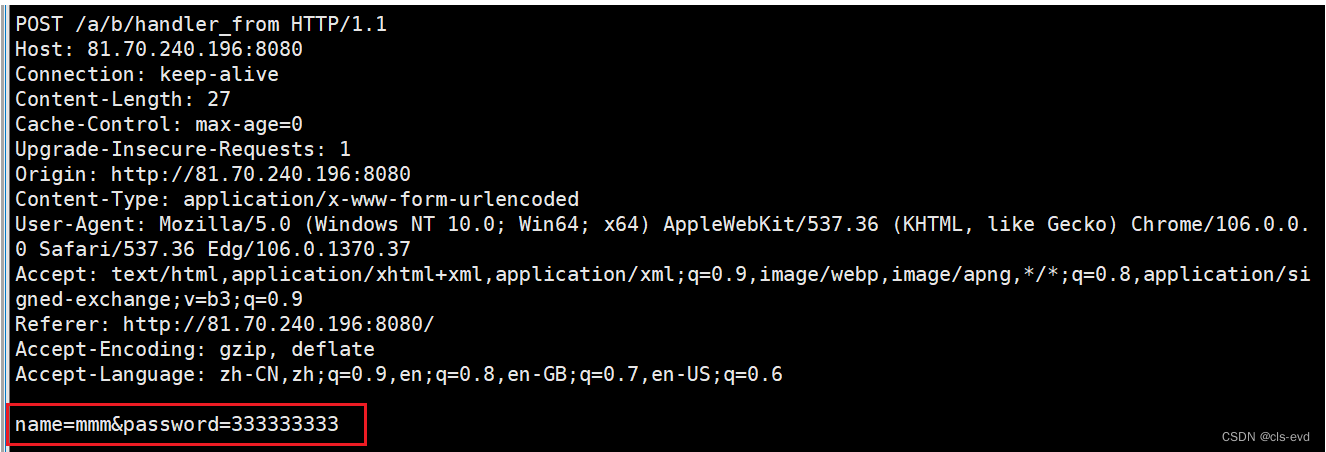
POST方法
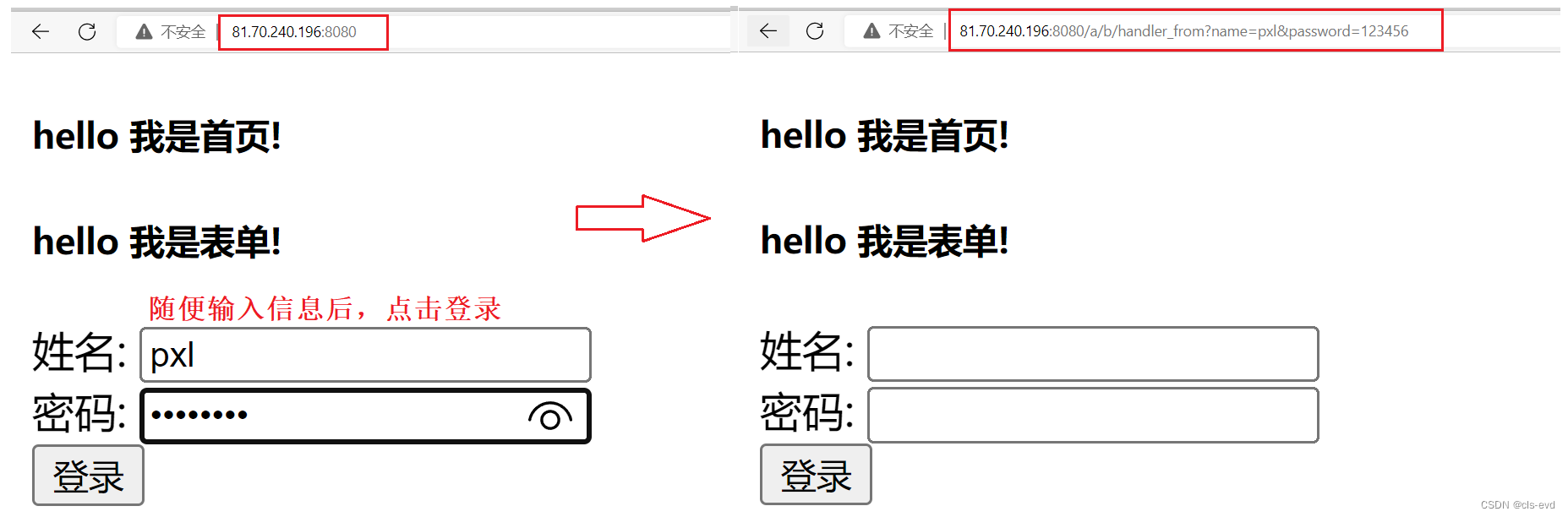
我们直接将method改成POST
这次我们发现上面什么也没有。
我们查看下服务器的请求
POST请求的资源还是在URL中,但是它的参数在正文当中,所以POST方法是通过提交正文提交参数的。
GET和POST的区别
这就是GET和POST的区别。GET和POST都可以提交参数,只不过,GET是将参数拼接到URL后的,POST是通过正文提交参数的。
通过抓包观察GET与POST
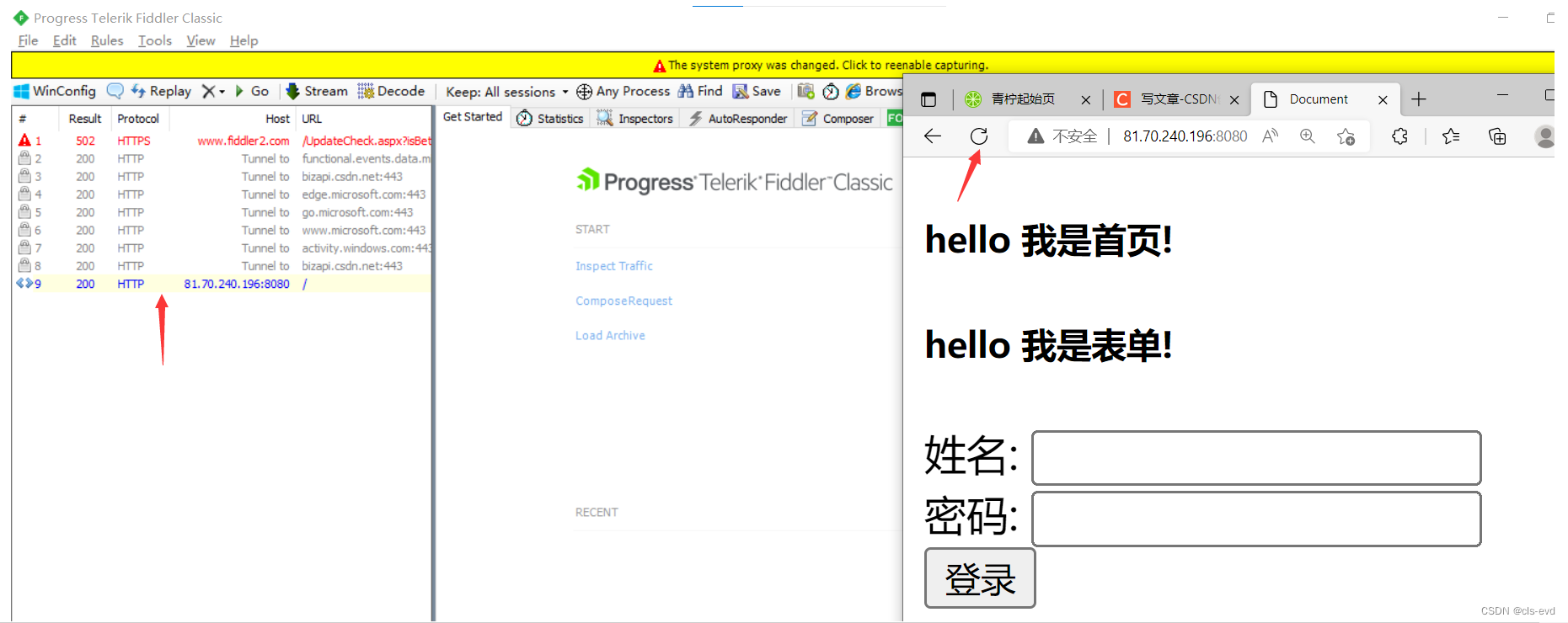
接下来我们使用Fiddler Classic工具,这是一个抓包工具,它是可以抓http的
我们直接打开该工具,刷新下我们自己的网页,就可以看到当前就抓到了第一个报文81.70.240.196:8080这个端口
双击后我们就能看到发起的请求及得到的响应
我们输入密码后进行登录
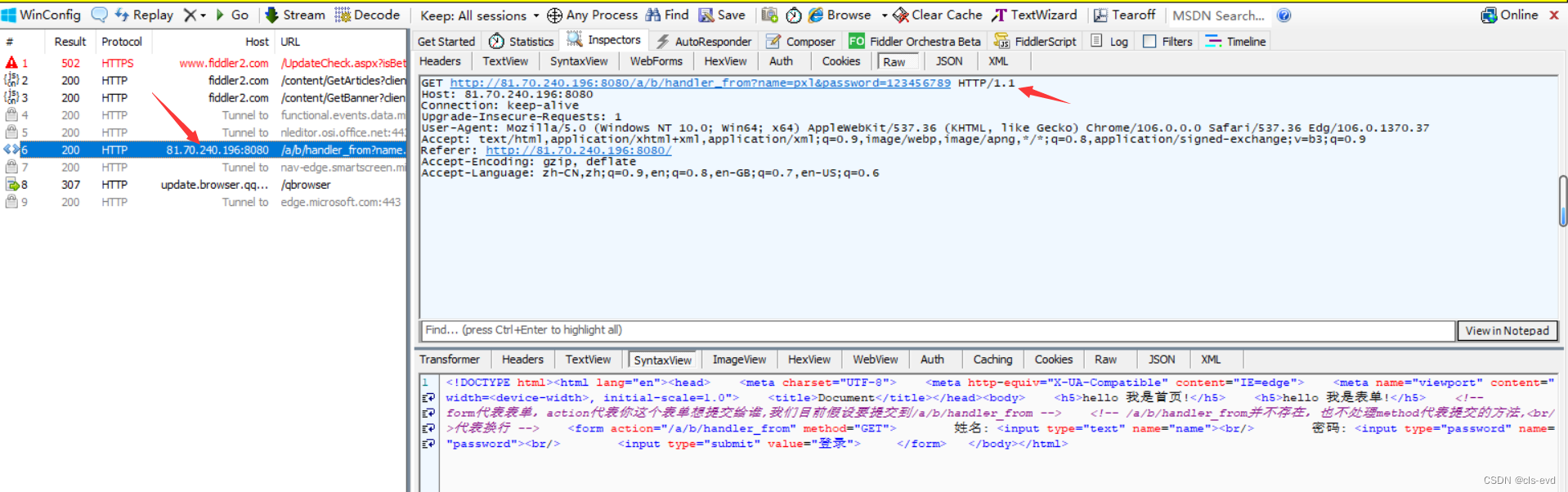
就能看到我们提交的请求,因为我们用的fiddler,所以它的URL那样显示。
抓包的原理
本来我的client直接请求服务器,服务器直接给client响应,现在变成了我的client先把请求交给fiddler,然后fiddler在帮我们去请求,server给的响应再给fiddler,fiddler再给我们的client对应的浏览器,所以所有的http请求都会流经fiddler,所以fiddler就可以抓包。因为fiddler要帮助客户端去请求server,所以它的URL显示的是该样式,http://81.70.240.196:8080/a/b/handler_from 前面就是我的公网ip,因为它要给我请求。
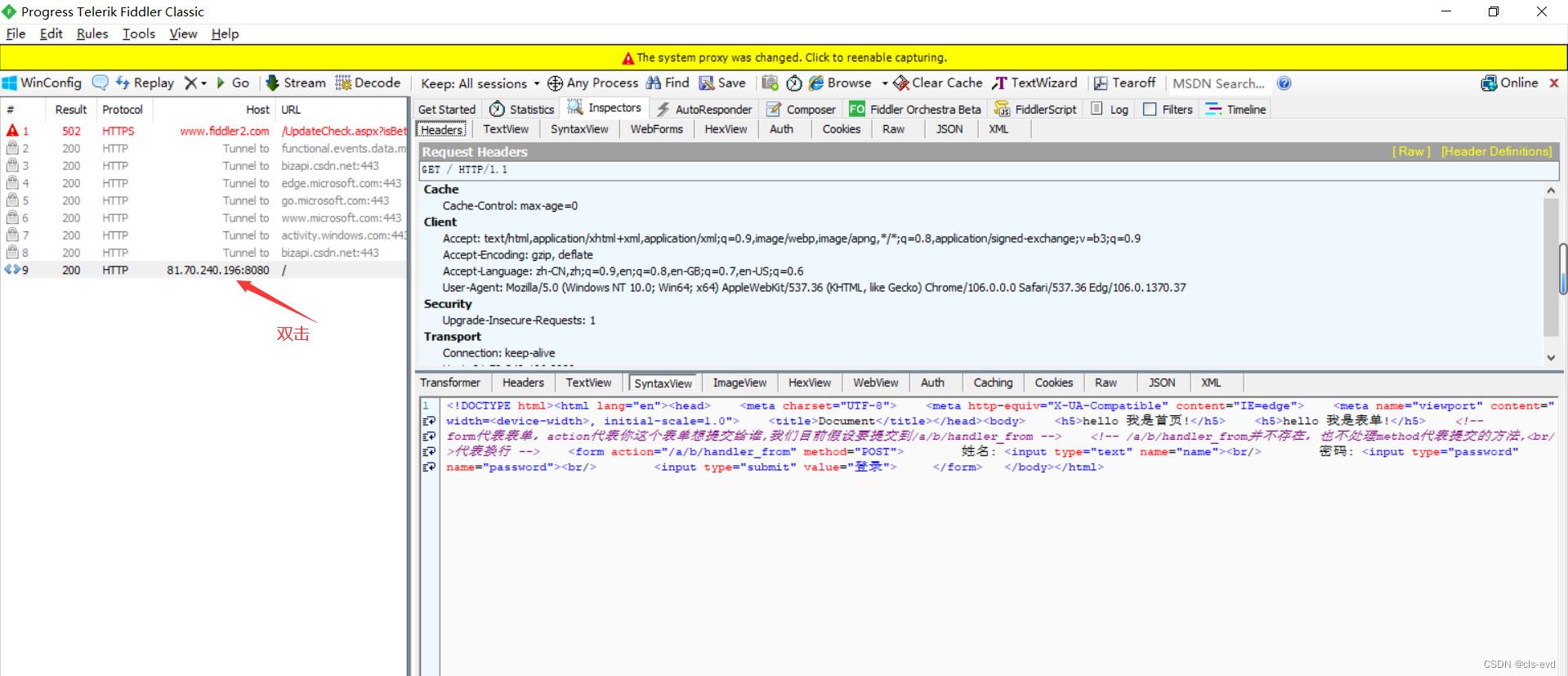
fiddler查看POST 方法

fiddler查看GET
同样我们输入用户名,密码后进行登录
这个就是GET方法,fiddler把参数都抓到了,正文部分没有。
总结:首先请求的时候,请求的是什么资源都是会出现在URL当中,只不过POST和GET传参,如果你进行提取参数的时候,通常参数的位置是不一样的,GET就在URL后,POST在正文部分。
GET和PSOT
概念问题
GET方法叫做,获取,是最常用的方法。默认一般获取所有的网页,都是GET方法,但是如果GET要提交参数(它也是可以进行提交的),是通过URL来进行参数拼接从而提供给server端。
POST方法叫做,推送,是提交参数比较常用的方法,但是如果提交参数,一般是通过正文部分提交的,但是你不要忘记,Content-Length:XXX 表示参数的长度
区别
参数的提交位置不同
1.参数提交的位置不同,POST方法比较私密(但是私密!=安全,很多人说POST传参更安全,这种说法是错误的,因为我们通过了fiddler抓包工具把他的数据给抓到了)因为它不会回显到浏览器的URL输入框!GET方法不私密,它是会将重要信息回显到URL的输入框中,增加了被盗取的风险。并不代表POST方法就没有被盗取的风险,所有在网络里传送的数据,没有经过加密,全部都是不安全的,随时都会被人直接扒出来。安全对我们来讲就是要进行加密!!!
2.GET是通过URL传参的,而URL是有大小限制的!和具体的浏览器有关!比如有的浏览器只允许你输入1024个长度的URL,那么你在请求时超过他就没办法显示了。POST方法,是由正文部分传参的,一般大小没有限制。
如何选择
1.GET:如果提交的参数不敏感,数量非常少,可以采用GET,
2.POST:提交的参数敏感,数量多,可以采用POST
所以选择时以GET为主,GET顶不住了,选用POST。
ps:HEAD方法就是当一个请求读上来后就是在buffer里面,当我知道它是HEAD以后,我把响应响应回去,正文部分不给他就可以了。
当我们在浏览器中输入数据,这叫做前端数据,当你一登录,以GET或者POST方法提交参数,那么这个参数不管是在URL当中,还是在正文里面,一定会保存到我们读取到的buffer里面。所以http协议处理,本质是文本分析。
所谓的文本分析
1.0 http协议本身的字段,比如:将你的第一行拿出来,空行一分,拆出来你的请求方法,请求的URL,请求的版本;空行之前的所有内容:kv值把他放在一个map里,我们就有了一个kv的请求报头。
2.0提取参数,如果有的话。有可能客户端是给我们提取参数的,最大的变化是前端的数据经过表单提交直接被你的C++程序,或者其他语言读到。读到之后就将前端数据,转换成了后端语言。然后我们就可以用后端语言处理。GET或者POST其实是前后端交互的一个重要方式。
HTTP常见的状态码
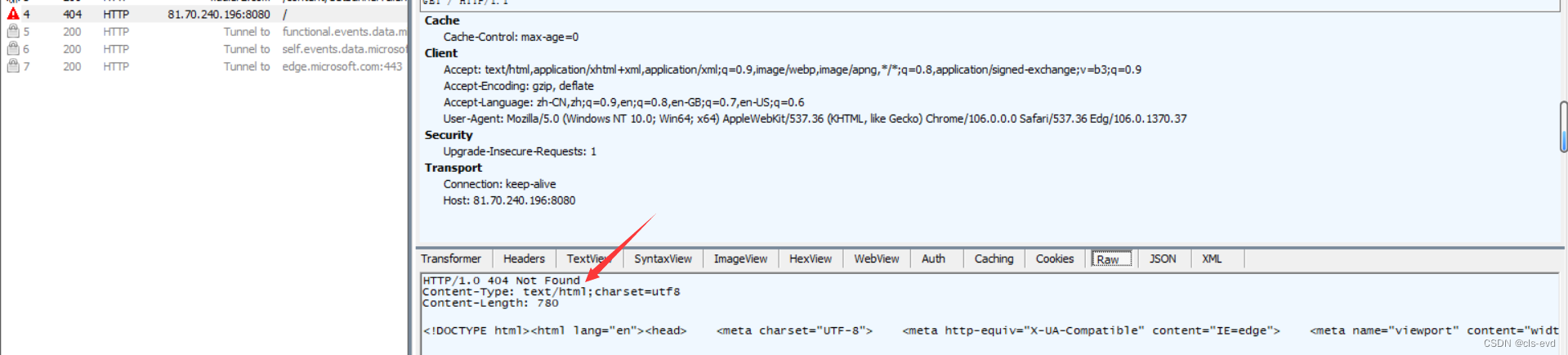
应用层是人要参与的,人的水平参差不齐,http的状态码,很多的人,根本就不清楚如何使用,又因为浏览器的种类太多了,导致大家可能对状态码的支持并不是特别好。
比如:我们把我们代码的响应的状态码改成404,状态描述改为Not Found;
我们通过fiddler看到响应是404 Not Found
但是访问服务器的时候,仍然是正常显示的,并没有做任何处理
类似于404的状态码,对浏览器没有任何的指导意义,浏览器就是正常的显示你的网页,你返回的网页是什么我就给你显示什么,浏览器不根据404做显示。
eg:类似于这种我们发现访问失联的网页并不是浏览器给你显示的,而是服务器给你显示的。也就是浏览器对404不做处理,就做一个正常的页面显示就完了。
具有指导意义的状态码
但是也存在一些状态码对我们是有指导意义的。
- 1开头的状态码,表示请求正在处理, 比如服务器收到一个请求,服务器处理要花很长时间,它要给你返回一个响应,就相当于说客户端不要着急,这个请求正在处理。1开头的用的非常少。
- 2开头最常见的是200(OK-请求正常处理完毕)。
- 3开头的状态码叫做重定向,有301,302,307,308。
- 4开头的最典型的是403(Forbidden禁止访问),404(Not Found)我们要处理404这种错误不要指望浏览器,而是说如果是404错误就需要自己进行处理,比如如果404,那么你就应该有一个404的相关处理,当你请求的资源不存在,你的服务器就应该构建一个正常的响应,告诉客户端我不存在。
- 5开头的状态码,表示服务器内部错误,最典型的右500,503,504。
eg:手动写一个404
我们将代码进行修改,专门弄一个不存在的路径
#include"Sock.hpp" #include<pthread.h> #include<sys/types.h> #include<sys/stat.h> #include<unistd.h> #include<fstream>#define WWWROOT "./wwwroot/" #define HOME_PAGE "index.html-back"// 其中wwwroot就叫做web根目录,wwwroot目录下放置的内容,都叫做资源! // wwwroot目录下的index.html就叫做网站的首页 void Usage(std::string proc) {std::cout << "Usage: " << proc << "port" << std::endl; }void *HandlerHttpRequest(void *args) {int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));// 这种读法是不正确的,只不过现在没有被暴露出来罢了ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer; //查看http的请求格式// std::string http_response = "http/1.0 200 OK\n";//版本,状态码,状态码描述,\n做结尾 这就是状态行// //在我看来就是一个长字符串,所以不用一行一行发,只要构建好,一块发出去就可// http_response += "Content-Type: text/plain\n"; //text/plain:正文是普通的文本 这就是响应报头// http_response += "\n"; //这就是空行,用来区分报头和有效载荷// http_response += "Shi Jiayi is a beautiful and hard-working girl"; //这就是正文// send(sock, http_response.c_str(), http_response.size(), 0);std::string html_file = WWWROOT; //访问的文件在这个路径下html_file += HOME_PAGE;//接下来才是正文std::ifstream in(html_file);if(!in.is_open()){std::string http_response = "http/1.0 404 Not Found\n";http_response += "Content-Type:text/html;charset=utf8\n"; http_response += "\n"; //空行http_response += "<html><p>你访问的资源不存在</p><html>";send(sock, http_response.c_str(), http_response.size(), 0); //响应回去}else{struct stat st;stat(html_file.c_str(), &st);//返回的时候,不仅仅返回正文网页信息,而是还要包括http的请求std::string http_response = "http/1.0 200 OK\n";// Content-Type 代表正文部分的数据类型,今天我们响应回去的不是字符串,而是把web服务器的根目录的// index.html响应回去。http_response += "Content-Type:text/html;charset=utf8\n";http_response += "Content-Length: ";http_response += std::to_string(st.st_size);http_response += "\n";http_response += "\n"; //空行std::string content; //正文内容std::string line; while(std::getline(in,line)) //按行读取 {content += line; //正文就全部在content里面了。}http_response += content;in.close();send(sock, http_response.c_str(), http_response.size(), 0); //响应回去}}close(sock);return nullptr; }int main(int argc, char *argv[]) {if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}} }
404的错误属于客户端问题,还是服务器问题?
404的错误属于客户端的问题,就好比你去京东去看抖音短视频,你请求的资源在京东服务器上是没有的。只要一个网站的资源是具体的,那么他一定是有限的,只要是有限的就一定会碰到没有的 资源。
服务器的问题有哪些呢?
比如:今天来了个新请求,创建线程失败了。处理请求时因为代码里存在问题,而导致程序崩溃,等等与服务器逻辑有关的错误,客服端请求是常规请求,但你服务器内部因为创建线程,创建进程...出错了,这就叫做服务器出错。
这就是5开头的状态码,表示服务器内部错误,最典型的右500,503,504。
3开头的状态码
3XX的状态码是有特殊含义的,3开头的状态码主要是叫做重定向。
重定向:
1.永久重定向 301
2.临时重定向 302或者307
重定向是什么?
当访问某一个网站的时候,会让我们跳转到另一个网址;
当我访问某种资源的时候,提示我登录,跳转到了登录页面,输入完毕密码,登录的时候,会自动跳转回来(登录,美团下单,)。比如你在淘宝上买个东西,你下单支付后,会告诉你支付成功,然后说3秒内,网页会自动跳转回去,你可选择立即跳转,你不管的时候,3秒以后它就会自动跳转回去。像这种现象,我们都叫做重定向。
比如:在访问力扣的时候,力扣想把老的网址废弃掉,让我们使用新的网址。如果它直接把老网站封掉,这样就会让很多老用户以为网站没了,所以力扣就在网站上做处理,直接访问新网址没有问题,访问老网站时会自动跳转到新网站(只不过力扣选择的是让我们手动点击跳转到新网站)这就叫做重定向。
什么叫做永久重定向,什么叫做临时重定向?
因为老网址的服务器配置太低了,所以我改了,改成新网站了。但是其他的老的用户只认识老网站,我不能直接把老网站关掉。所以我就在老网站的服务器中做了一个永久重定向。意思就是说,现在有3个老用户,依旧习惯访问老网站,当他访问时,老网站的服务器不对他们提供服务,而是直接告诉老用户,你请求的已经不是我了,而是叫做www.new.com,请你访问这个网站,所以这个客户不需要知道,它的浏览器会自动向新网站重新发起请求,然后新网站重新得到响应给用户提供服务。如果用户将来还想访问老网站,那么这种永久重定向会把用户以前记录的,比如说书签,你添加的这个书签是在浏览器里添加的,当浏览器收到,这个是永久重定向,除了让浏览器访问新网站后,还要浏览器把用户记录的书签,由新的域名替换调旧的域名。以后用户点击书签,就会直接去访问新网站,再也不访问就网站了。
永久性重定向通常用来进行网站搬迁,域名更换。对我们来讲就相当于,把以前的服务全部迁到了新网站上面,然后在老的服务上,添加一个重定向功能,然后一个客户来的时候,老的服务器不提供服务,直接通过永久性重定向告诉浏览器说我已近搬到最新的地方了。然后在更新下本地浏览器的缓存的一些数据,包括书签,当用户再次点击书签的时候,就可以跳转到新网站,不在访问老网站,随着老用户不断去访问旧网站,最后用户就全部被切换到了新网站中。这就是永久重定向。
比如说:我今天在美团上下单,支付成功了, 就提示我支付已经成功,正在返回中,我从A页面,跳转到支付页面,支付成功后又返回到B页面(商家接单的页面),但是对我们来讲一定是从一个页面跳转到另外一个页面,而且每次下单都有如此操作。这个跳转是为了完成某种业务的需求,比如我进行注册后,要给用户提供一个注册页面,注册成功后要返回到登录页面,登录成功后返回到首页,当每一次登录或者注册成功,不需要你自己手动的再去回到登录或注册首页,而是服务器自动让你回去。每次登录注册都需要重复做这个工作,属于业务的环节。这种情况就是临时重定向。
模拟重定向
重定向是需要浏览器给我们提供支持的,浏览器必须识别310,302,307这样的状态码。server要告诉浏览器,我应该再去哪里。http响应的报头属性,Location:新的地址
eg:服务器构建响应的时候,状态码是301,描述是永久重定向,Location:告诉我要重定向到哪里,我们以重定向到腾讯的官网。访问我的时候就直接跳转到腾讯。

完整代码
#include"Sock.hpp"
#include<pthread.h>
#include<sys/types.h>
#include<sys/stat.h>
#include<unistd.h>
#include<fstream>#define WWWROOT "./wwwroot/"
#define HOME_PAGE "index.html-back"// 其中wwwroot就叫做web根目录,wwwroot目录下放置的内容,都叫做资源!
// wwwroot目录下的index.html就叫做网站的首页
void Usage(std::string proc)
{std::cout << "Usage: " << proc << "port" << std::endl;
}void *HandlerHttpRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));// 这种读法是不正确的,只不过现在没有被暴露出来罢了ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer; //查看http的请求格式std::string response = "http/1.1 301 Permanently moved\n";response += "Location:https://www.qq.com/\n";response += "\n";send(sock, response.c_str(), response.size(), 0);}close(sock);return nullptr;
}int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}}
}测试:
从fiddler看出,别人给服务器请求,服务器给一个响应,直接就是301,永久重定向,Location填的就是腾讯官网,此时就直接跳转到了腾讯的官网,
这个过程对我们来讲,我们并不知道,你以为你当前访问的是这个服务器,实际上自动就别浏览器跳转到了新的网站。
测试302,临时重定向



永久重定向遗留的问题

做完301永久重定向这个实验后,我们会发现自己的浏览器把这个服务器端口记住了(这点还体现在你的服务端,只有第一次访问域名,服务器出现请求,之后多次进行访问,服务器并未出现任何请求),不管你的服务端时候运行,只要你访问这个域名就会直接给你重定向到腾讯官网,如何解决?
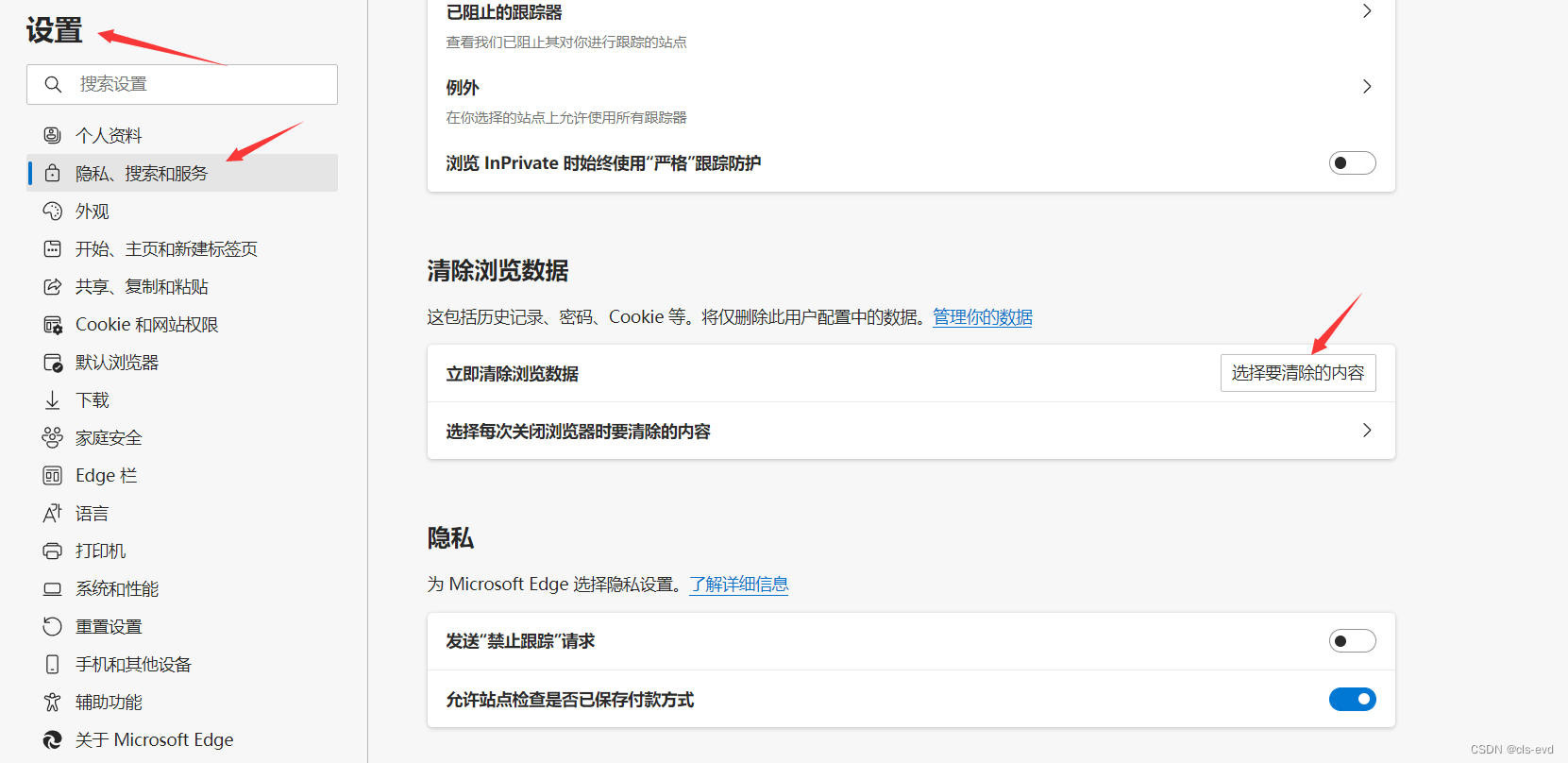
我们只需要清除一下301重定向这段时间内的浏览器缓存即可,博主的浏览器是Edge 。清除的内容不需要手动选择,浏览器默认的即可。清楚完毕后,我们就发现我们的域名不在进行重定向了。
再谈HTTP常见Header
- Content-Type: 数据类型(text/html等)
- Content-Length: Body的长度
- Host: 客户端告知服务器, 所请求的资源是在哪个主机的哪个端口上;
- User-Agent: 声明用户的操作系统和浏览器版本信息;
- referer: 当前页面是从哪个页面跳转过来的;
- location: 搭配3xx状态码使用, 告诉客户端接下来要去哪里访问;
- Cookie: 用于在客户端存储少量信息. 通常用于实现会话(session)的功能;
我们之前的所有实验,全部都是请求,响应,断开链接,服务器上有很多资源。
一个大型的网页内部,是由非常多个资源组成的!!!每个资源都要发起http请求!!!这个就是基于短连接的策略。所有http/1.0叫做短连接。http/1.1之后,我们引入了长链接。其中客户端发起请求要设置一个Connection字段,叫做Keep-alive叫做保持活,说白了就是这个连接要一直使用,长连接服务端构建响应也要包括Connection,双方就任务我们都是1.1以上的版本,就都用长连接,这样的话,双方通信时复用同一个连接,此时就不用再打开连接,关闭连接。这样的成本就降低了。
长连接与短连接
一般而言,一个大网页是由多个元素组成的。
短连接
http/1.0 采用的网络请求的方案是短连接。
短连接的运算规则:request->response->close。实际上进行一次http请求的时候,本质就是把你要访问的对应资源打开,返回一个资源,这个资源可能是一张网页,可能是网页里面的一张图片,可能是一个视频等。所以如果网页由多个元素构成,那么一次请求只返回一个资源,在访问一个由多个元素构成的网页的时候,如果是http/1.0,就需要多次进行http请求,比如我的网页构成里面有100个元素,此时就要重复的进行http的100次请求,而http协议是基于tcp协议的,tcp要通信必须执行以下步骤: 建立连接->传送数据->断开链接。每一次的http请求都要执行该步骤,整体比较耗时间,效率不高。短连接的效率比较低,所以就诞生了长连接的概念,http/1.1支持长连接。
服务端有一张网页,这个网页里面又有很多很多的其他资源,比如图片之类的。当我们的一个客户端发起请求的时候,它请求到这个网页,这个网页给他进行返回,返回之后,客户端拿到了这个网页本身,我们发现这个网页里面有很多的,包含第三方的链接或者另外一些资源,客户端发现这些资源还是在你的服务器上,所以客户端不断的进行请求和响应,得到多份资源,最后经过不断的重复请求连接得到对应的资源构建的一个网页,这叫做短连接。
长连接
长连接:建立好一条连接,双方进行请求,响应的时候都用这一条连接,就能把这个网站中的所用的各种资源全部拿下来,拿下来的时候,这条连接始终不关闭,这种技术就称之为长连接。
长连接主要解决的就是每一次请求都要进行请求建立tcp请求,而导致每一次请求资源都要重新建立连接这样的频繁建立连接的过程。长连接通过减少频繁建立tcp连接,来达到提高效率的目的!我们虽然不知道tcp如何建立连接,但是我们写tcp套接字,我们的客户端必须得connect,当connect成功,才必须进行后序访问(之前我们的实验中connect都很快,这是因为你的服务器资源本身只有你一个人用,没有人和你抢,还有就是你connect的次数并不多),如果tcp请求的频率特别高,然后连接建立的次数太频繁其实就会降低我们的效率,而我们通过长连接就可以直接通过一个连接把网页的所有资源得到,在浏览器中构建一个完整的网页。
Connection

有可能双方有一方不支持长连接,我们就可以通过报头里Connection这个选项,Connection如果携带了Keep-Alive表示它支持长连接。有时候没有这个Connection选项,或者这个选项是close,就代表它不支持长连接,只支持短连接。
类比生活中的例子:我现在要让你办5件事情,我通知第一件事情,我给你打一个电话,打完电话一挂,过来一会,我在给你打第二个电话,以此类推,让你办5件事情,就给你打5次电话,这5次电话,每一次都要重新给你拨号,然后你接通之后,我们两建立连接成功,在进行沟通对应的一件事情;现在变成了我给你打一次电话,你不要挂电话,然后一个电话就把5件事情全部说完了,这就是长连接。
cookie 与 session
背景引入
现实生活中,很多地方我们用的都是http协议,比如:我们登录某些网站,然后你会发现,你把浏览器关掉了,或者直接把网页关掉了,过一会再重复的访问这个网站的时候,第一次需要你进行账号,密码的登录,但是第二次,第三次在访问这个网站的时候,你就不需要在输入账号密码,就能直接登入了。
http协议本身是一种无状态的协议!就代表它很简单。
在比如我们打开一个视频网站,我要看一个电影,但是这个电影是VIP才能看的,我登录账号以后,这个视频网站是如何知道我是不是VIP呢?如果是VIP就直接播放电影,不是VIP就不能播放电影。
我们的日常经验:在网站中,网站是认识我的。当我访问一个网页就是发起了一次新的http请求,我打开一部电影也一定是跳转到一个新的网页中。各种页面跳转的时候,本质就是进行各种http请求,这个网站照样认识我!
但是http协议本身是一种无状态的协议,它的无状态的含义就是今天我发起第一次http请求,那么再发起第二次请求,这两次请求对于http的客户端和服务器来讲,它不知道曾经发起了第一次,也不关心即将发起的第二次,只关心当前次干了什么,也就是http协议它并不记录我们发起这次http请求的上下文信息,谁发的?什么时候发的?历史上有没有发过?全部都不关心,http只关心本次请求有没有成功,对历史上的请求,它不做任何的记录,这就叫做无状态。
问题引入
目前。上述两个知识比较矛盾,
1.经验告诉我们,你今天进行各种页面跳转,本质就是发起了各种http请求,让我们得到网页的内容,但是我们发现不管怎么跳转,网站都是认识我们的,我是不是VIP它一看就知道。
2.http协议本身是一种无状态的,也就是说http协议,它压根就不知道发起这次http请求的是谁,历史上这个人有没有发起过,历史上它发起的内容有哪些,通通不关心,每一次http请求就是从最原生的方式帮我们继续重新请求资源,历史上的信息它从来不记录,也就是说http请求,在任何一次请求的时候,都不知道是谁发起的请求,只要告诉我你要访问谁就可以了。
eg:你的男朋友容易失忆,你今天和他一起玩了,但是第二天他就不认识你的,去了什么地方,你是谁,他都不认识,因为你的男朋友不记录历史数据,他只记录这次谁陪我去玩了。这就是无状态。
Cookie
对我们来讲,http是不记录上下文的是无状态的,那网站是如何认识我的呢?
当我请求各种各样新的网页的时候,有的视频就是需要VIP才能播放的,我登录的时候,只是在登录页面发起http请求,当我再去访问新的VIP视频的时候,它怎么能认识我呢?
我们肯定是有新的技术保证客户始终在线,网站认识我并不是http协议本身要解决的问题,网站认识我和http无状态是两种层面上的东西,让网站认识我,http可以提供技术支持(但是我的http照样是无状态的),来保证网站具有“会话保持”的功能。说白了,假设今天的网站有10000个网页,http的角度这就是10000个网页,每个网页都是独立的,站在网站的视角,就是我要知道谁都访问了哪些网页。
我们让网站认识我,实际是一种cookie技术,cookie主要是用来做“会话保持的”,会话保持更高级的说法叫做"会话管理"。
会话与会话管理
会话:我们登录xshell的时候,输入账号,密码,xshell就认识我了,其中我登录的时候,就叫做一个建立会话的过程。
会话管理:同样的,我们登录一个网站的时候,一旦登录成功,网站记录你的个人信息,让你在这个网站中可以进行各种你的权限范围之内的各种资源访问,这就叫做会话管理。
http的核心功能主要是帮助我们解决网络资源获取的问题,这些会话保持的功能本身http不给你彻底解决,但是我可以给你提供技术支持,会话保持就需要你自己解决。
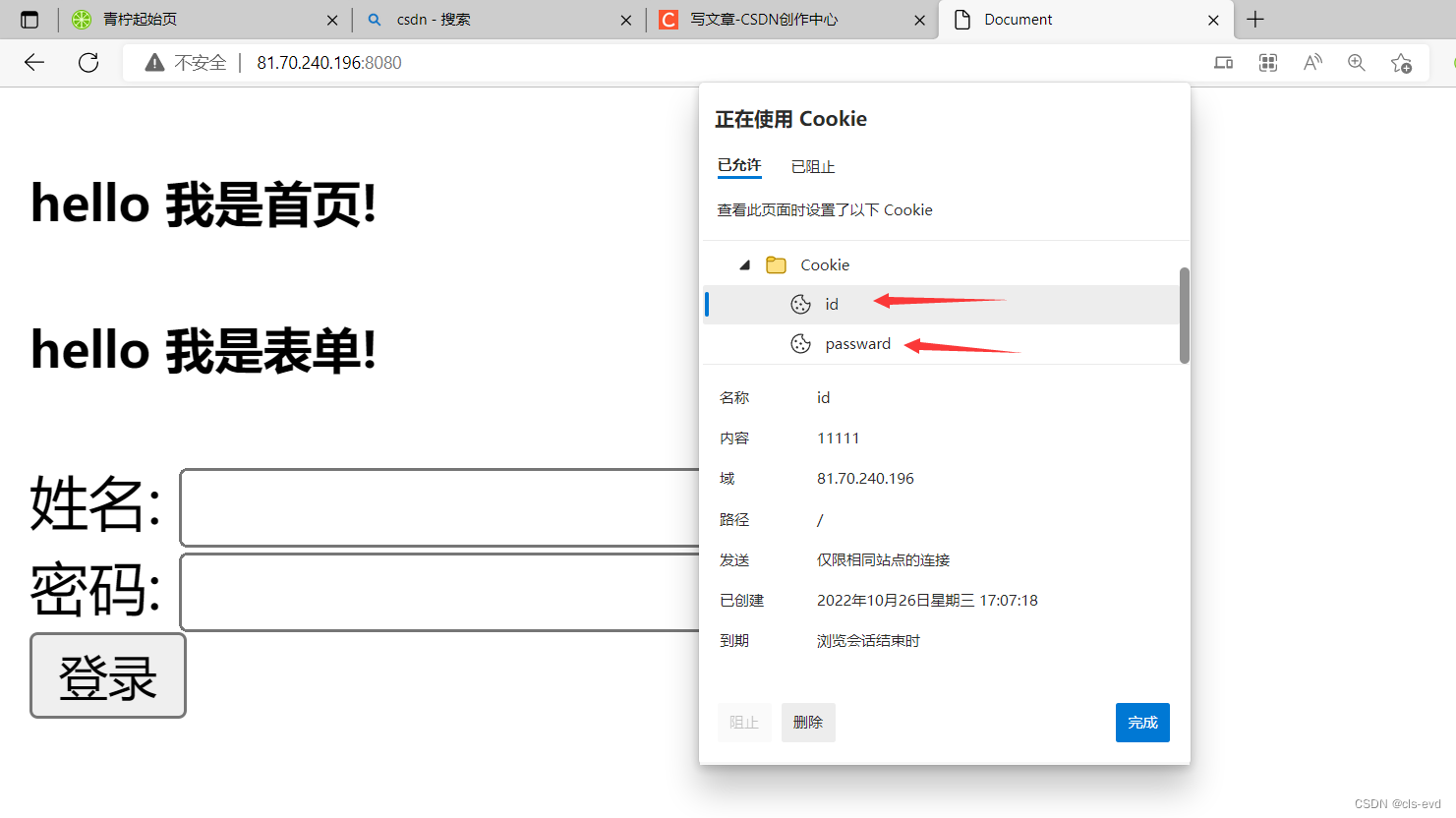
eg:我当前的b站是处于登录状态的,关闭网页后,在打开还是登录状态,但是我将它的cookie信息删除
再次刷新页面网站就不认识我了,就需要我们再次登录了
刚刚的cookie就能决定网站是否认识我。
cookie
1.浏览器角度:cookie是一个文件(这个文件在浏览器中),该文件里面保存的是我们的用户的私密信息。
2.http协议角度:一旦该网站对应有cookie,在发起任何请求的时候,都会自动在request中携带该cookie信息!!!
我们进行登录注册的时候,服务器端得到用户名和密码,后端经过认证,登录成功。然后浏览器内部会形成一个cookie文件,里面保存的就是username和password,一旦登录成功,说明这次输入的用户名和密码是合法的,浏览器就把服务器认证成功的用户名和密码写到这个cookie文件中。后续的请求,每一个请求的请求报头属性,都会自动携带对应的cookie。
意思就是说:你一旦第一次登录成功,登录成功认证之后,浏览器自动会把你登录成功的用户名,密码写在一个cookie文件里,后续所有的读写请求都会在自己的请求报头属性里都会自动携带上对应的cookie,也就是它会把这个cookie里面的username,password这样的字段携带上,然后每一次都会发送给这个server,所以server就可以每一次针对你访问的所有请求,因为你自动就携带了用户名,密码,所以在后端,没访问一个网页,每对应一个网页都可以进行用户名,密码的认证,只有你通过了,server在给你响应回你的请求,如果认证不通过,就告诉你这个视频是VIP要看到,你看不了。或者你得先登录,登录后才能看。浏览器会自动帮你在请求的报头属性里携带这个cookie。所以服务器在后续请求时,就认识了你。以上是基本理解,仅仅是为了理解,实际上我们现在很少有情况是把用户名,密码保存到cookie。
验证cookie
Set-Cookie:服务器向浏览器设置一个cookie。当我们一旦使用了这样包含Set-Cookie这样的选项这样的请求返回给浏览器时,就是在指挥浏览器,让浏览器帮我把Set-Cookie后面的内容,写在你自己的cookie文件里,从此往后,你每次向我请求时,都把这个信息带上。
Sock.hpp
#pragma once#include<iostream>
#include<string>
#include<cstring>
#include<cstdlib>
#include<sys/socket.h>
#include<netinet/in.h>
#include<arpa/inet.h>
#include<unistd.h>using namespace std;
class Sock
{
public:static int Socket(){int sock = socket(AF_INET, SOCK_STREAM, 0);if (sock < 0){cerr << "socket error" << endl;exit(2); //直接终止进程}return sock;}static void Bind(int sock,uint16_t port){struct sockaddr_in local;local.sin_family = AF_INET;local.sin_port = htons(port);local.sin_addr.s_addr = INADDR_ANY;if (bind(sock, (struct sockaddr *)&local, sizeof(local)) < 0){cerr<<"bind error!"<<endl;exit(3);}}static void Listen(int sock){if (listen(sock, 5) < 0){cerr << "listen error !" << endl;exit(4);}}static int Accept(int sock){struct sockaddr_in peer; //对端的信息socklen_t len = sizeof(peer);int fd = accept(sock, (struct sockaddr *)&peer, &len);if (fd >= 0){return fd;}return -1;}static void Connect(int sock, std::string ip, uint16_t port){struct sockaddr_in server;memset(&server, 0, sizeof(server));server.sin_family = AF_INET;server.sin_port = htons(port);server.sin_addr.s_addr = inet_addr(ip.c_str());if (connect(sock, (struct sockaddr*)&server, sizeof(server)) == 0){cout << "Connect Success!" << endl;}else{cout << "Connect Failed!" << endl;exit(5);}}
};Http.cc
#include"Sock.hpp"
#include<pthread.h>
#include<sys/types.h>
#include<sys/stat.h>
#include<unistd.h>
#include<fstream>#define WWWROOT "./wwwroot/"
#define HOME_PAGE "index.html"// 其中wwwroot就叫做web根目录,wwwroot目录下放置的内容,都叫做资源!
// wwwroot目录下的index.html就叫做网站的首页
void Usage(std::string proc)
{std::cout << "Usage: " << proc << "port" << std::endl;
}void *HandlerHttpRequest(void *args)
{int sock = *(int *)args;delete (int *)args;pthread_detach(pthread_self());#define SIZE 1024*10char buffer[SIZE];memset(buffer, 0, sizeof(buffer));// 这种读法是不正确的,只不过现在没有被暴露出来罢了ssize_t s = recv(sock, buffer, sizeof(buffer), 0);if (s > 0){buffer[s] = 0;std::cout << buffer; //查看http的请求格式std::string html_file = WWWROOT; //访问的文件在这个路径下html_file += HOME_PAGE;//接下来才是正文std::ifstream in(html_file);if(!in.is_open()){std::string http_response = "http/1.0 404 Not Found\n";http_response += "Content-Type:text/html;charset=utf8\n"; http_response += "\n"; //空行http_response += "<html><p>你访问的资源不存在</p><html>";send(sock, http_response.c_str(), http_response.size(), 0); //响应回去}else{struct stat st;stat(html_file.c_str(), &st);//返回的时候,不仅仅返回正文网页信息,而是还要包括http的请求std::string http_response = "http/1.0 200 OK\n";// Content-Type 代表正文部分的数据类型,今天我们响应回去的不是字符串,而是把web服务器的根目录的// index.html响应回去。http_response += "Content-Type:text/html;charset=utf8\n";http_response += "Content-Length: ";http_response += std::to_string(st.st_size);http_response += "\n";http_response += "\n"; //空行std::string content; //正文内容std::string line; while(std::getline(in,line)) //按行读取 {content += line; //正文就全部在content里面了。}http_response += content;in.close();send(sock, http_response.c_str(), http_response.size(), 0); //响应回去}}close(sock);return nullptr;
}int main(int argc, char *argv[])
{if (argc != 2){Usage(argv[0]);exit(1);}uint16_t port = atoi(argv[1]);int listen_sock = Sock::Socket();Sock::Bind(listen_sock, port);Sock::Listen(listen_sock);for ( ; ; ){int sock = Sock::Accept(listen_sock);if (sock > 0){pthread_t pid;int *parm = new int(sock);pthread_create(&pid, nullptr, HandlerHttpRequest, parm);}}
}首先我们不加 Set-Cookie
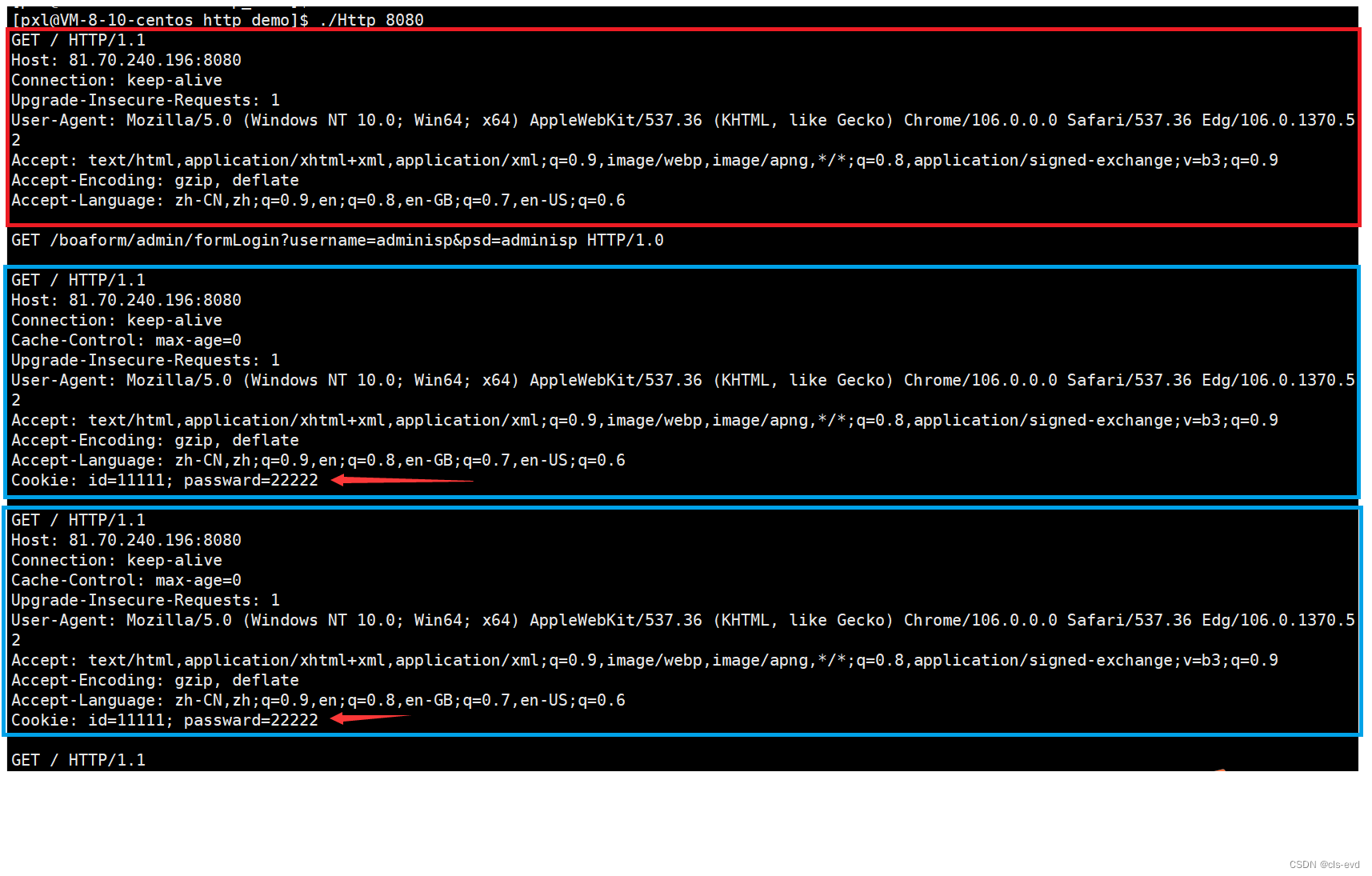
我们看到cookie是空的,没有任何的cookie信息
添加cookie
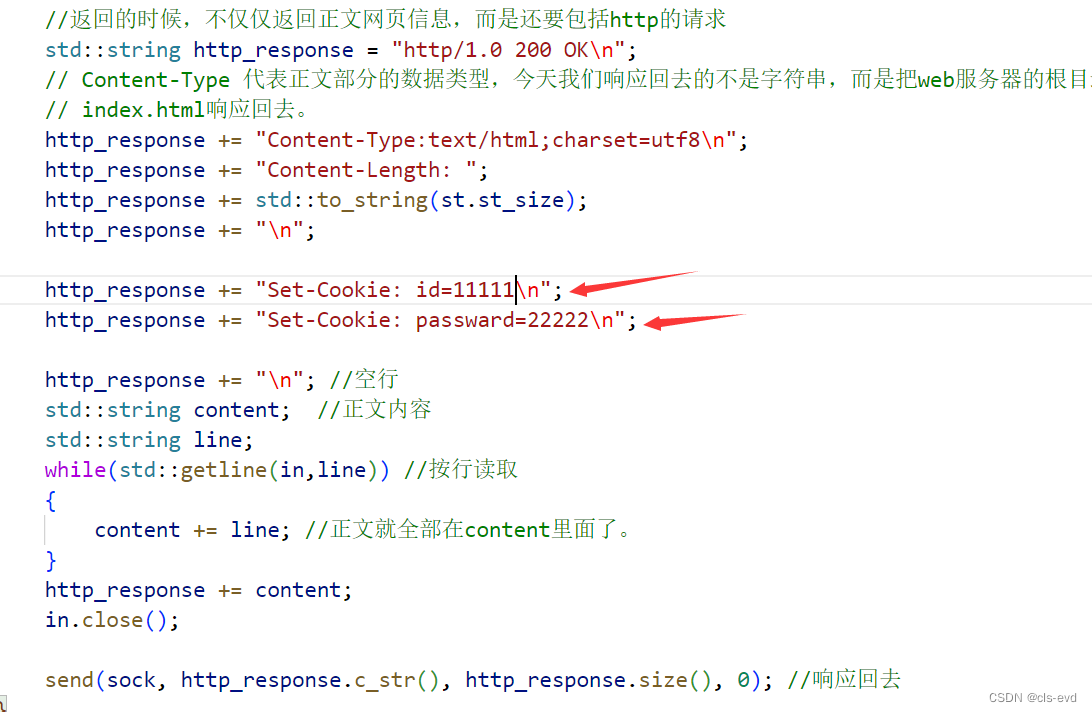 至此,我们就添加了一个cookie ,这个Set-Cookie就是我们在响应报头里添加的报头属性,id=...就是我们要设置进文件中的内容,\n代表它是一行。
至此,我们就添加了一个cookie ,这个Set-Cookie就是我们在响应报头里添加的报头属性,id=...就是我们要设置进文件中的内容,\n代表它是一行。
我们访问我们的服务器,就看到了两个cookie
然后我们在多刷新几次这个网页。
我们发现第一次,访问这个网页,正常请求,然后进行Set-Cookie,然后浏览器就包含了cookie信息,然后从第二次访问开始,在进行刷新的时候,我们就会发现请求中就会带上Cookie属性。以后每一次请求,浏览器都会自动检查你访问的这个网站,也叫作你访问的域,只要这里有cookie都会自动给你把cookie携带上。
所以只要你访问的是目标的网站,浏览器会自动把你曾经给这个目标网站对应的浏览器内部写入的cookie信息给你携带上,作为请求的一部分。你想设置cookie,我们的选项就是Set-Cookie: ...
你登录任何网站的时候,只要你登录上了,一定会有cookie正在使用,如果你不想让他认识你了,你把这个cookie信息移除掉,再次刷新网页,它就不认识你了,如果你把这个cookie一直保留着,此时对应的浏览器向任何目标网站发起对应请求时,请求里面都会携带上Cookie字段,然后支持服务后端对你的身份进行多次认证,每一次都要进行认证。
类比生活:当客户端第一次请求时,服务端说给你个工牌,你把它保存好,以后你再出入我这个服务器的时候,你都把这个工牌带上,客户端说:好的。再比如:你去了腾讯,当你入职第一天,你的领导就给你一个工牌,以后进公司就没有人拦住你了,第一次请求的时候就相当于你入职的过程,往后你每天上班,带着你的工牌,也就是每次发起请求,服务端也就是保安总是认识你,因为它发现你带着工牌,它可以核实你的信息。这就是为什么网站认识我。
cookie文件的存在形式
它有两种存在形式:
1.文件版,如果是在文件中,那么它就是在浏览器的安装目录下,以及它使用的某些相关的用户级目录下,他会把用户对应的cookie信息保存在文件里。即便你把电脑关了,你再去访问目标网站,这个cookie信息他还能知道。
2.内存版,意思就是说,浏览器一关闭,访问的目标网站就不认识你了。
cookie的安全问题
我今天把登录把账号密码输入给服务器,服务器认证通过后,给我返回登录成功请求,然后我本地就把账号,密码这样的私密信息更新到cookie里面,包括我的浏览痕迹等。目前最私密的就是账号,密码。如果今天我不小心点击了恶意网站,这些恶意网站今天向我的浏览器端注入了一些木马程序,盗取了我的cookie文件,然后别人把这个cookie文件放在他自己浏览器的特定目录下,然后访问和我访问一样的网址,此时因为有cookie信息了,他就可以以我的身份访问目标网站了。所以这就是大部分人被盗取账号的底层重要的理论。
如果别人盗取我的cookie文件有两个安全问题:
1.别人可以以我的身份进行认证访问特定的资源
2.cookie如果保存的是我的用户名和密码,那么这个账号就直接泄露了。
单纯使用cookie是具有一定的安全隐患的。
比如:你自己的账号经常被盗。当你在你的电脑上登录QQ 的时候,QQ的服务器是如何知道你是登录状态,它如何维持它的会话保持呢,包括你只要登录上你的QQ,我要访问QQ邮箱等一些其他功能,基本上都是以我当前的这个账号就进行访问了,也就是访问其他功能就不需要我再次输入账号密码了。QQ的好多功能都是相互打通的,就是因为你在登录你的账号的时候,它也会形成对应的cookie信息保存在它自己的服务当中。就比如你访问QQ空间,然后就自动打开了浏览器,浏览器为什么知道是你这个人的QQ空间而不是其他人的,说明你在登录状态打开QQ空间的时候,QQ的请求就自带cookie信息了,说明cookie信息早就被保留了。这也说明当你在访问恶意网站的时候,别人盗取了你的cookie信息,别人就可以以你的身份访问你的QQ空间了,甚至登录你的QQ,然后就可以访问你的资源了。
别人盗取我们的cookie信息现在仍然存在,信息泄露的问题也是永远解决不了的,安全级别更高,那么攻击手段就越强。所以才有了各种各样的杀毒软件,对我们的软件进行保护,我们的服务器也有自己的安全策略,但是这样的问题依旧避免不了,只要用cookie,信息就有泄露的风险。
这两个问题,最严重的是第二个问题,我的身份认证信息泄露了其实也不影响,比如你的QQ被盗了,以你的身份行骗,但是你的人际关系不好,没有人借给你钱,这样也算从另一个维度保护了账号安全。最严重的是个人私密信息泄露了,用户名,密码,浏览痕迹都会被泄露,这是很危险的,我们要想办法把这些私密的信息保留起来的,所以我们今天有了一个新的技术,就叫做session。
现在市面上主流的使用方式是cookie+session。但是session是没法举例的,因为session的实现是需要服务端有更多的实现方案的,session的代码量太大了,我们没办法实现。
session
核心思路:将用户的私密信息,保存在服务端。
为什么私密信息会被盗取呢?
因为你是个普通小白,作为普通的用户,你的私密信息是所有的恶意分子想要的并且你的防护级别很低。所以有些人就喜欢安装些杀毒软件,但是这些软件的级别也不够。因此衍生出session。
当你登录某个网站的时候,一定携带用户名+密码,服务端首先就要先认证,认证通过之后,构建一个响应告诉你认证通过了,客户端这里就可以通过服务端给的Set-Cookie命令,然后把个人认证的信息保存起来。这是我们刚刚所说的。
session处理策略
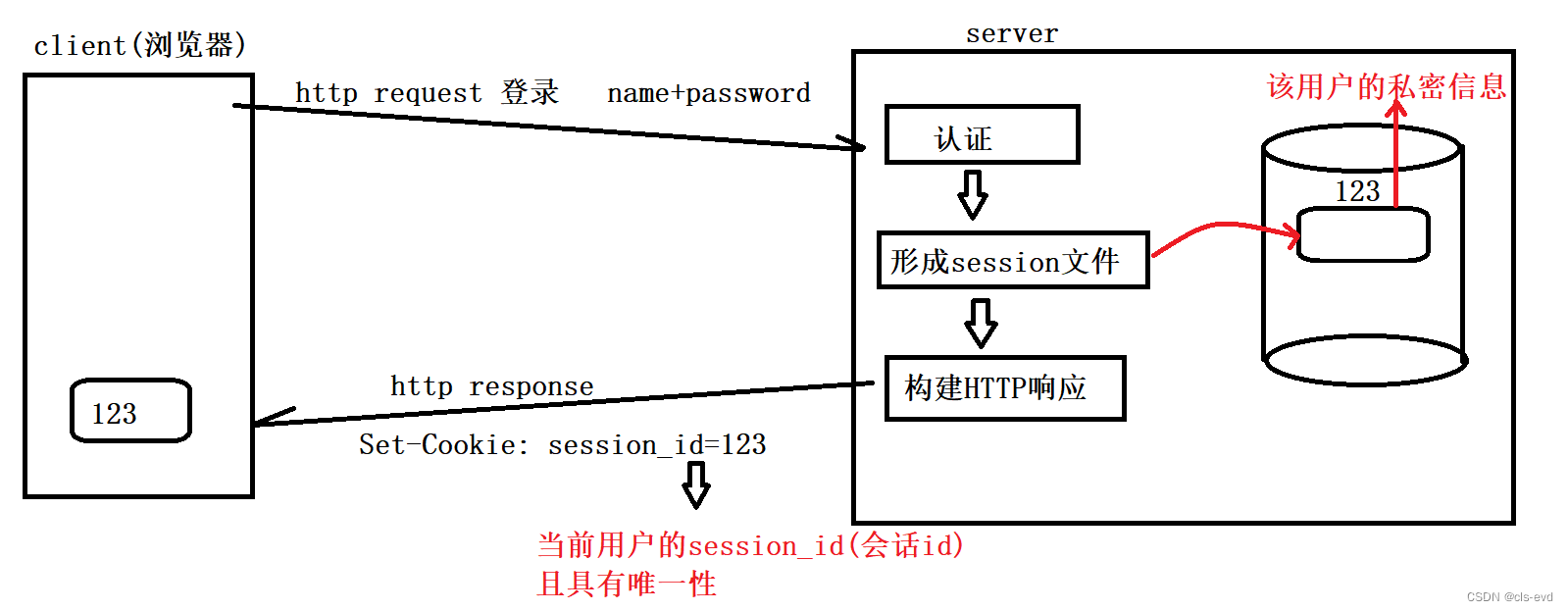
现在,服务端认证通过后,在服务端的磁盘上(直接理解成linux的目录中)就形成一个session文件,这个session文件比如说叫做123,这个文件里面保存的就是该用户的私密信息,用户名,密码,浏览痕迹...然后服务端进行构建http响应,构建响应的时候,需要设置Set-Cookie:session_id=123。换言之,依旧会给客户写回一个cookie值,这个cookie值照样会正常的保存在浏览器的cookie文件中,只不过这次保存的cookie文件里面,只有一个数字,叫做123,我们把这个123称为当前用户的会话id(session id)。如果这个网站有100个人访问,那么每一个人都要形成一个session文件,这个文件的文件名必须具有唯一性,所以这里的session id 在服务端一定是一个具有唯一性的值。也就是有100个人,每一个人都会形成唯一的session文件,每个人的session id都不一样,这个是可以通过算法解决的(比如文件名,我们就可以把时间戳带上,然后给每个人添加一个递增编号,组和就形成了唯一值)。此时响应回去照样写cookie,只不过这次的cookie里面保存的就是用户对应的session id。所以后续所有的关于server的访问,所有的http请求,都会由浏览器自动携带cookie文件中内容(就是当前用户的session id)。当服务端搜到客户发来的session id ,它对用户的身份认证,就不在需要用户名,密码了,只需要确定session id 有没有在服务端中,只要通过session id找到对应的文件,就能找到用户的私密信息,从而对用户做认证。后续,server依旧可以做到认识client,这也是一种会话保持的功能。换言之,我们应该看到所有的客户端访问服务器上所有的请求,包括看所有视频,所有的网页,只要你曾经登录过,往后server端就可以根据你的session id来确认你的存在。
cookie安全的第一个问题
因为客户端的cookie里面不在保存用户任何的私密信息,所以也就杜绝了,即便是用户他将自己的cookie文件泄露了,也不会导致用户的私人信息被泄露。但是,我们还有cookie文件被泄露的风险,这个问题是无法被杜绝的,因为这个cookie文件是在用户的电脑上,用户没有防护意识,用户电脑上它被盗取几乎是必然的,所以是没有办法解决的。这也就是为什么腾讯这么大的公司,它的QQ照样还能被人盗取,解决不了。
cookie安全的相关策略
cookie文件被泄露了,别人拿着我的cookie文件去访问曾经这个cookie对应的网址,别人就冒充我的身份了,这个也是只能解决cookie安全的第二个问题,cookie安全的第一个问题照样没法解决。
但是可以有一些衍生的防御方案了。比如:你的QQ,如果你跨越地区了,你的QQ就会提示你当前QQ登录地点异常,请确认是否是本人操作,包括用一台新设备登录也是如此...这是因为ip地址是可以确认出地域的,比如:最近的好多软件,如果你评论的话是会显示你的对应的地址的,这就是通过ip的归属处理的,不同种类的ip隶属不同的片区,所以通过ip就能确认地区。每次登录QQ就对你的ip做认证,如果你的QQ被盗了,假如你是山西的,盗取你QQ号的人是缅甸的,那么1分钟前你还在山西,1分钟后你就在缅甸了,此时QQ就立马识别到用户异常,然后让你重新登录,让你重新登录的本质是废弃掉刚刚的session id,重新给你形成新的session id。所以一旦重新登录了,对端的session id也就失效了。
再比如:如果我是一个不法分子,我盗取了你的账号,以你的身份访问了某些网站,我最想做的事情不是立马试试诈骗,我最想做的就是把你这个人的用户名和密码改掉,让这个账号永远是我的了,但是这种情况是不可能存在的,因为诞生了一个新的设备--手机,所以以前没手机的时候,我们用的是邮箱认证,现在有手机了,如果你要改密码,第一件事情永远是输入旧密码,第二件事情如果你的登录地址有异常,或者它的审核标准比较严,还需要你进行短信认证。也就是数据层面上你把cookie文件丢了,但是手机没丢,即便是手机也丢了,手机和cookie都被同一个人拿走了,你手机也有密码。短信上面的认证,就相当于,即便你的信息被盗取了,他要改你密码,他也改不了,这也就是一般你的账号被泄露或者盗取,我们经常说的申诉,就是重新认证你,因为是账号的拥有者,当初绑定的是你的手机号,所以最后可以通过手机进行二次认证,使别人盗取到的cookie信息失效就可以了。所以只要session id是server去指派的,它的session id管理工作是由server去做的,虽然你的客户端保留了一个session id,但是server随时可以让这个session id失效,让别人盗取也没有意义,所以就可以有各种各样的策略,比如异地登录,短信认证,包括QQ检查内容,一旦发现有些账号有异常行为,比如频繁添加好友...侦测之后,就可以强制用户下线,强制用户下线也很简单,只要在服务端把对应的session 文件干掉。这就是cookie与session。
再谈http无状态
再来看看最开始的问题,网站是认识我的,但是http是一种无状态的协议,也就是你请求什么网页,请求前,请求后和我没关系,http只是你告诉我要什么,我给你拿什么,哪怕是上次刚要过,这次还要要,我也会给你拿,这就是http的无状态,它不记录用户的任何行为,但是网站是需要认识这个用户的。
为什么网站需要认证用户,也就是为什么登录这个网站的时候它需要永久的认识用户呢?
因为http无状态,所以今天你登录成功了,如果我的网站不认识你,你只在访问该页面的时候,它认识你,但是我一旦点击一个新的页面,查看一个新的视频,那么对不起,你要先输入用户名和密码你才能看,你要手动进行一次认证,换言之,引入cookie+session本质就是为了提高用户访问网站或者平台的体验!你只要登录我的网站,所有内容你都可以随便访问,当然增强用户体验就是上下文要记录用户的状态,而http是无状态的,所有就有了cookie和session来解决这个问题。
HTTPS
http的信息在互联网中传送基本就是数据在互联网中裸奔,别人想在随时随地想抓取你的数据就能抓取。局域网通信本质上就是你发收到数据和你在同一个局域网的所有人都能够看到,只不过别人不处理罢了,所以局域网通信本质就相当于有两个人在自认为双方在通信,实际上有一大批吃瓜群众在 围观,如果你不加密数据本来就是在裸奔,这也就是不管用POST还是GET方法都解决不了的,我们只能对网络数据进行加密。自从中国互联网因为以前的互联网巨头出现了很严重的安全隐患,我们国家的互联网从安全领域就变的越来越重视了,现在你访问的所有网站都是HTTPS
eg:你现在能叫上名字的所有网站全部是HTTPS
像我们自己搭建的浏览器就提示是不安全的
背景认识一
https其实是http+TLS/SSL。TSL/SSL简单的理解成http数据的加密解密层,这一层也是软件层。

我们使用http然后直接使用系统调用就叫做http,如果我们使用http,然后向下访问时不直接访问系统调用接口,而是访问一些安全相关的接口,然后再用安全访问的相关层在访问系统调用接口,在把数据发出去,因为http的请求和响应都要经过这个加密解密层,所以请求时完成了加密,响应时完成了解密,这个协议就叫做HTTPS。因为这里的TLS/SSL是属于应用层协议,也就是说它只会在客户端和server端两端出现,换言之也就意味着我们的数据在网络中总是被加密的(对于下三层数据是没有被加密的,也不需要,你加密主要是为了保护用户的隐私,所以只要把应用层数据加密就可以了)到了对端,对端向上贯穿的时候也会自动进行解密,所以同样的在http依旧是请求和响应,就是加了一层软件层。
实际上在网络里,是整个http请求+有效载荷被全部加密了,当然有些版本只对有效载荷加密,因为http本身就是一些私密信息,但只要服务器和客户端双方认识就可以,其实http的报头也可能包含用户私密信息(eg:session id),一般是对整个http进行加密,加密后交付给下层去传输,然后到对端解密,出来之后就是http,相当于在同层看来依旧正常通信,没有加密解密的过程。
背景认识二(数据的加密方式)
1.对称加密
这里有个秘钥的概念,这个秘钥只有一个,比如说秘钥是X,所谓的对称秘钥就是用X加密,也要用X解密。就像你家里的门钥匙,锁门你用这个钥匙,开门也用这个钥匙。
假设现在有个数据data;
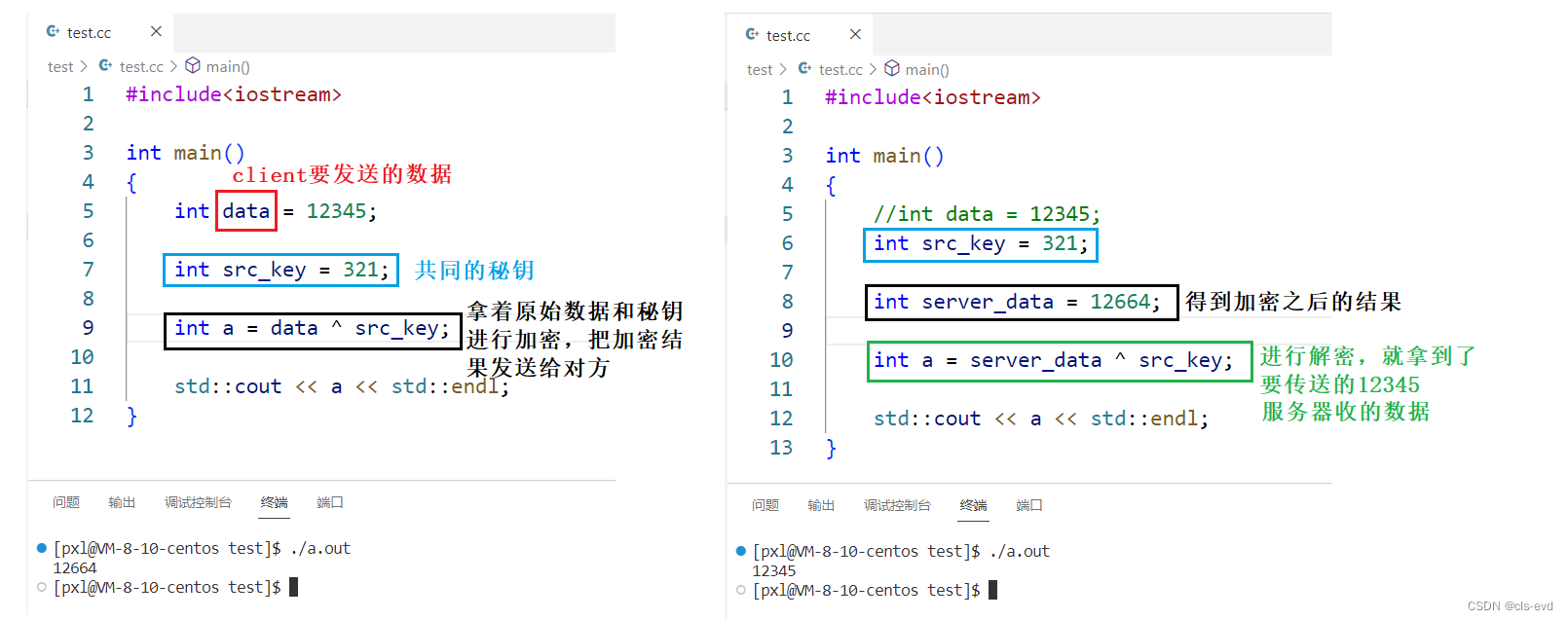
data 异或 X = result;
X 异或 data = result;
你要发的数据是12345,实际发的是12644,服务端收到后进行解密就是12345。所以曾经学的异或运算,让不同数字异或同一个值(src_key),这样的src_key就称之为对称秘钥。
对称加密就是使用同一把秘钥进行加密,解密。异或其实就是一种简单的加密算法。
2.非对称加密
有一对秘钥:分别叫做公钥和私钥。可以用公钥加密,但是只能用私钥解密;如果用私钥加密,只能用公钥解密。你必须用一个加密,另一个解密,这就叫做非对称加密,最典型的非对称加密算法常见的就是RSA。
一般而言,公钥是全世界公开的,私钥是必须自己进行私有保存的!也就是私钥不能暴露给外部,你必须自己保存起来。
背景认识三
假设现在有一篇论文,那么如何防止文本中的内容被篡改?以及识别到是否被篡改?
 我现在需要有一个方法来甄别是否有人改过这篇论文,哪怕是改过一个标点都不行。我们这篇文本的文本量是可大可小的,我们可以针对该文本进行Hash散列,形成固定长度,唯一的字符序列。这种算法的特点就是对文本进行任何改变,哪怕是一个标点符号,都会形成一个差异非常大的hash结果!也就是说,我选择的hash散列算法,如果文本有一点点不一样,那么形成的字符序列的变化就特别大。最典型的这样一个算法时md5。所以我们把这个固定长度,唯一的字符序列我们称之为数据摘要或者叫做数据指纹。然后我们再采用加密算法(一般是非对称的),我们将这个固定长度,唯一的字符序列在进行加密,得到加密结果,这个加密结果我们一般把它叫做数字签名。
我现在需要有一个方法来甄别是否有人改过这篇论文,哪怕是改过一个标点都不行。我们这篇文本的文本量是可大可小的,我们可以针对该文本进行Hash散列,形成固定长度,唯一的字符序列。这种算法的特点就是对文本进行任何改变,哪怕是一个标点符号,都会形成一个差异非常大的hash结果!也就是说,我选择的hash散列算法,如果文本有一点点不一样,那么形成的字符序列的变化就特别大。最典型的这样一个算法时md5。所以我们把这个固定长度,唯一的字符序列我们称之为数据摘要或者叫做数据指纹。然后我们再采用加密算法(一般是非对称的),我们将这个固定长度,唯一的字符序列在进行加密,得到加密结果,这个加密结果我们一般把它叫做数字签名。
我是一个通信端,我现在要发送这段文本,我怎么保证这段文本没有被篡改?
我就可以在发送的文本当中把原始文本带上,另外在文本的尾部带上该文本的数据签名,最后在我们在网络里,就把它俩作为一个整体发送出去,当接受端收到数据,就要确认这个文本是否被篡改。

校验
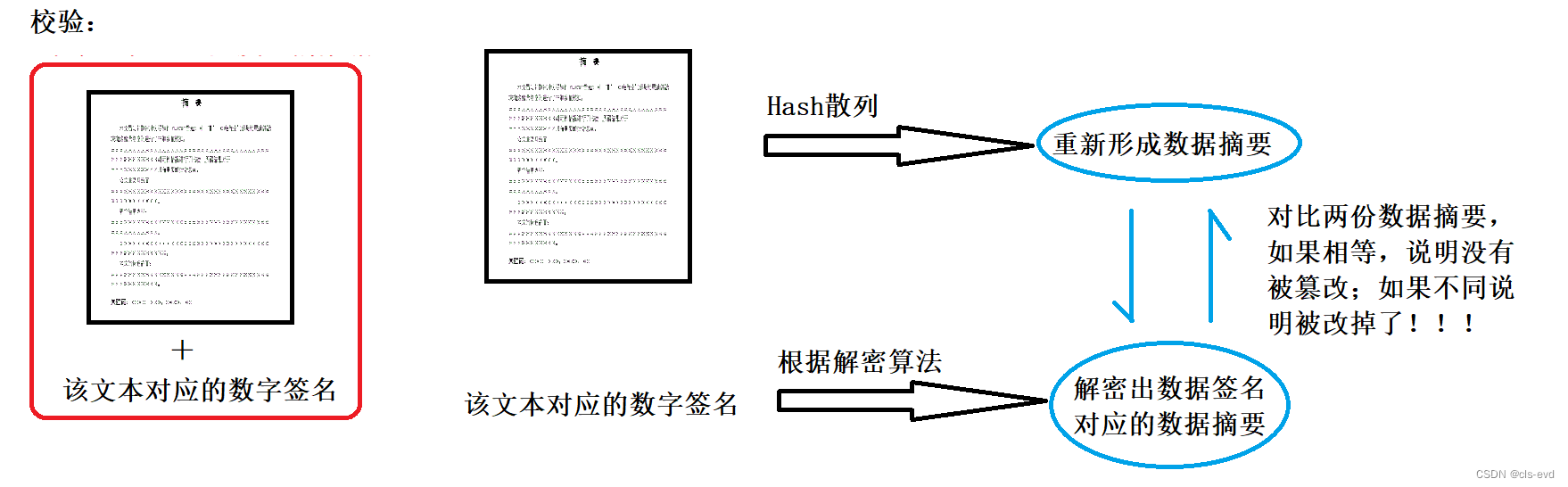
1.从接收到的数据中把原始文本拿出来,紧接着对原始文本采用相同的hash散列,对于这段文本重新形成数据摘要。
2.把数据签名拿出来,根据解密算法,把这个数据签名解密出数据签名对应的数据摘要。
然后对比两份数据摘要,如果相等,说明没有被篡改,如果不同说明被改掉了!
https是如何通信的呢
首先我们进行通信,双方的数据是必须得被加密的。既然加密,也必须解密。
如何选择加密算法
1.对称加密
2.非对称加密。
如果我们选择对称加密,假如客户端用X秘钥进行加密,那么server端怎样得知这里要用X秘钥解密呢,反过来也一样,如果server端给客户端发消息,server端用X秘钥加密,那么客户端如何得知X呢。
方案一
预装。也就是我们给服务端和客户端把世界上所有采用的对称加密的秘钥信息都给他俩预装好,在你开始买机器的时候,天然就有了,这样的话双方就可以直接用了。
但是这样有几个问题:
- 预装的成本太高了。
- 如果我没有预装,就得进行下载,我下载的时候就要把一些软件及秘钥的相关信息全部下载下来,还是在网络上跑。
- 既然这个信息已经被预装了,那么代表别人也能预装,如果你的秘钥是明文,那么别人也就知道了,如果你的秘钥是暗文,那么对这个暗文也需要进行解密,然后就有非常大的鸡生蛋,蛋生鸡的问题。
- 所以这个预装是非常的不靠谱的,是不行的。
方案二
对称加密
双方通信的时候协商秘钥。这种方案看起来可行,假设服务器现在并不知道秘钥是什么,客户端形成了一个秘钥X,然后因为是对称加密,所以它发过去的数据加密是需要被server知道的,所以它需要把自己的X交给https,所以就进行通信,但是第一次决定是没有加密的。就是说客户端告诉服务端,我要用X进行加密,我把X先给你,你一会用X进行解密,这里就特别搞笑,因为第一次传送第一条数据的时候,服务端还没有收到X,所以客户端不能进行加密,因为客户端一加密了,对方就不知道了,所以客户端的第一条消息必须是把秘钥以明文的方式发送过去,这里就很尴尬,我把秘钥以明文发送过去,如果这个秘钥信息被盗取了,后续双方进行加密通信就没有任何意义了。说明在刚开始通信时,协商秘钥阶段,采用对称加密的方式是根本不可能的。
秘钥协商,采用对称方式是绝对不可能的!
非对称加密
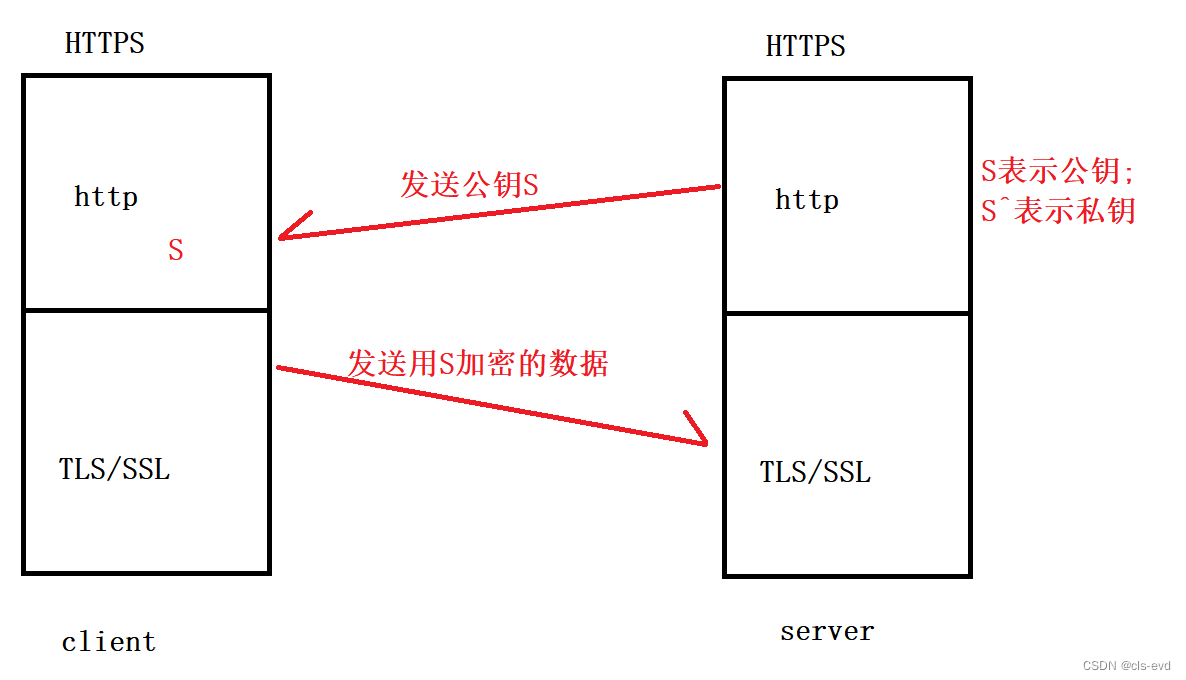
我们采用非对称方式加密,我们用S表示公钥,S^表示私钥。
当客户端请求服务端的时候,服务端首先进行秘钥协商,服务端把他的公钥S给客户端,此时客户端就拿到了一个公钥S,紧接着客户端拿到了公钥S之后,用公钥S对数据进行加密,此时客户端在把加密号的数据发送给服务端,所以客户端发出去的数据是用服务端提供的公钥S进行加密的。因为这个世界上只有server具有私钥S^,也就只有server能进行解密!如果其他人拿到了这个数据也是没办法的进行解密的,因为其他人没有私钥S^。此时服务端收到加密数据根据私钥S^,解密出data,就拿到了数据。换句话说就是server端把公钥暴露给了全世界,全世界的客户端都能拿到公钥,但是任何人拿到公钥一旦加密,那么除了服务端没有任何人可以解密。所以经过这样的方案,我们就能保证数据从客端传输到服务端的安全。但是从服务端到客户端,是不能用私钥S^加密的,因为一旦用私钥S^加密,那么只能用公钥S解密,可是全世界都知道公钥S,所以从服务端发送给客户端的数据就是不安全的。也就意味着如果只要一对公钥和私钥只能保证单向数据安全。
那么我们给客户端一对公钥和私钥,给服务端一对公钥和私钥,在通信阶段,提前交换双方的公钥,就能保证双向数据安全。
既然一对非对称秘钥,可以保证数据的单向安全,那么两对就可以保证数据的双向安全了。
两对非对称秘钥的问题
但是事实并非如此!!!
- 依旧有被非法窃取的风险,暂时先不谈。
- 非对称加密算法,特别费时间!就是因为这一点,这种方案就几乎已经不被采纳了。对称加密是比较省时间的。
所以在我们实际进行http通信的时候,我们根本就不是采用纯对称或者纯非对称,纯对称有安全隐患,纯非对称有效率问题。
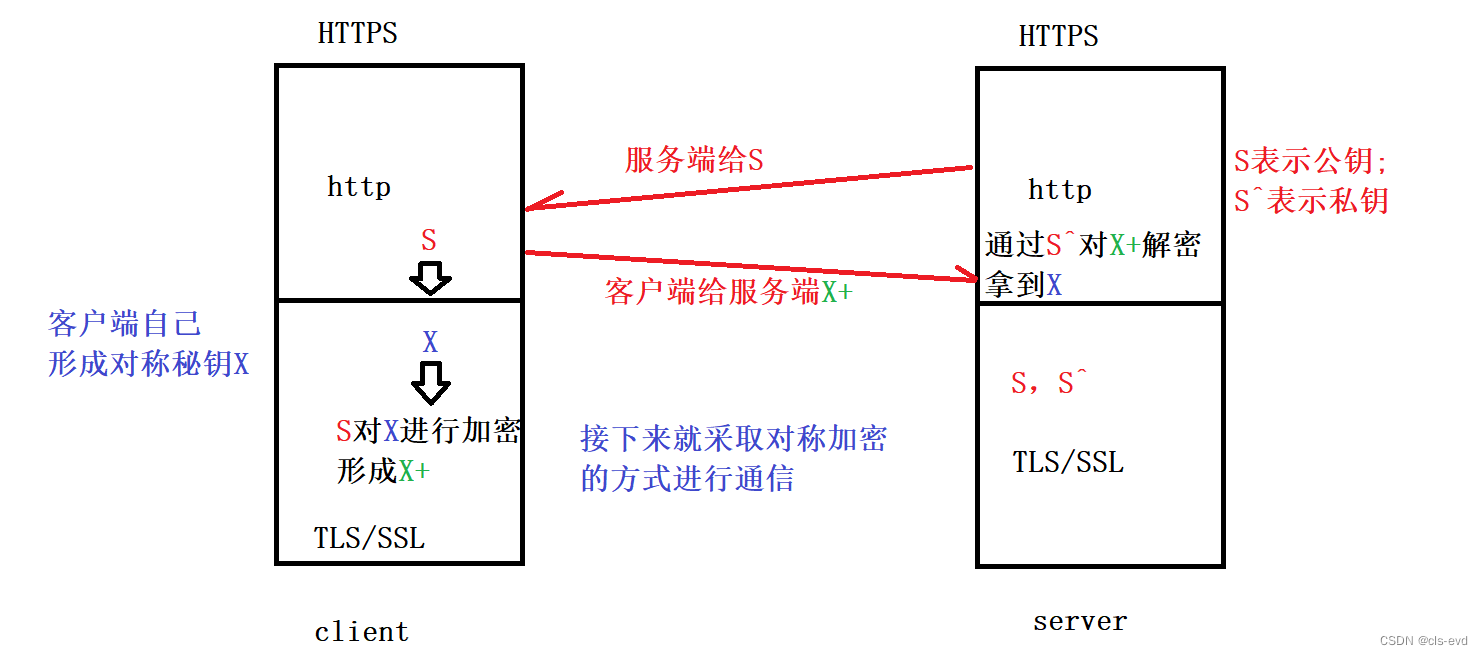
实际中的加密方法
实际中采用的是非对称+对称方案!
当客户端发来一个请求,服务端是有自己的非对称的公钥S和非对称的私钥S^的,当客户端一旦分发起请求,服务端给客户端进行响应的时候,服务端就将自己的公钥给客户端,客户端就收到了公钥S,接下来,客户端形成对称秘钥的私钥X,然后客户端用公钥S对私钥X进行加密形成X+,然后客户端把经过加密的对称秘钥的私钥交给服务端,这个世界只有服务端有S^,所以只有服务端能用S^对X+进行解密,然后就得到了X,所以server就以安全的方式拿到了客户端发来的对称秘钥的私钥X,然后这个阶段完成后,因为客户端和服务端都知道了对称加密的X,所以他俩就采用对称方案进行数据的加密和解密。
将对称秘钥发送个对方叫做秘钥协商阶段,采用非对称算法。
利用对称秘钥传输数据叫做数据通信阶段,采用对称加密。
什么叫做安全
不是让别人拿不到就叫做安全,而是别人拿到了,也没办法处理。只要别人有一点点可能性能侦测到你的数据,你就要把这种可能性无限放大,这就是安全意识,小小的漏洞都要认为它是一个普遍问题。你的数据是随时随地都能被别人抓到的。只要你的数据在网络里跑,别人据一定能拿到。现在的问题是数据加密了,能解开就是不安全的,解不开就是安全的 。
在安全层面,解密的成本远远超过了解密后带来的收益就是安全的。
比如:别人出价10块,让我破解你的信息,但是我破解你的信息要花费10000,如果我不考虑成本,我一定能破解,但此时考虑了成本,我是不会进行破解的,此时就称你的数据是安全的,因为我破解了是没有任何意义的。这是以经济角度谈的。如果信息涉及到了国家安全,那么它就不是钱能衡量的,那么这个时候它的安全级别必须是特别特别强的,你要攻克我,可能要用一些超级计算机得几百上千年才能运算出来,这也就是为什么我们国家搞的一种量子计算机国外非常害怕,因为量子计算的运算能力是比现在的二进制计算机的效率高了几万,几十万,甚至几百万倍,所以本来破解一个密码需要1个月,现在就可能只需要几秒钟,一瞬间就把你建立好的安全全部破解了。
中间人
客户端和服务端之间的数据被中间的某些用户查看,阅读,甚至篡改,这种攻击手法我们称之为中间人。
那么在服务端把公钥给客户端的时候,可不可能出现问题呢?
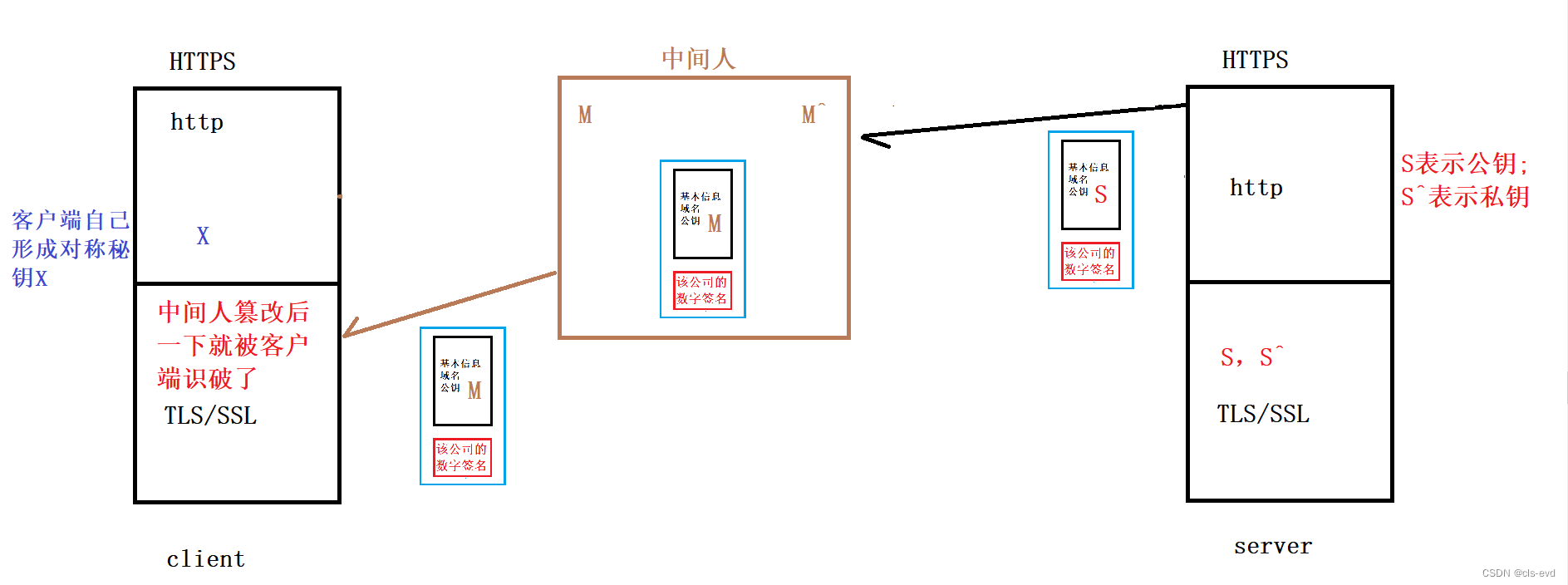
在网络环节中,随时都有可能存在中间人来,偷窥,修改我么的数据。服务端在给我们客户端发送自己的公钥S(这也是一段报文或者是一段数据),假设此时出现了个中间人(一台监听设备),这个设备内部也有自己的公钥M,私钥M^,服务端发送的公钥S,是大家随时随地都可以获取的,只不过这个中间人做了一个工作,它将服务端发送个客户端携带公钥S的报文拿到,然后把自己的公钥M替换了服务端的公钥S,然后把包含公钥M的这个报文发送给了客户端,此时客户端并不知道中间人把服务端发给自己的报文篡改了,所以客户端就认为自己收到了一个公钥M,然后形成自己的对称加密的私钥X,将X通过M进行加密形成M+,然后客户端就把M+发送给服务端,可是中间人又把这个M+截取到了,因为你用的是中间人的公钥M,所以中间人就用私钥M^进行解密,然后就拿到了客户端和服务端进行通信的对 称加密的私钥X。然后中间人就把这个私钥X保存在自己的系统里,然后把解密出的数据私钥X重新用公钥S加密形成S+,然后把这个S+在交给服务端,此时服务端和客户端都认为自己交换成功了自己的秘钥,可此时中间人也拿到了服务端和客户端通信对称加密的私钥X,这样中间人就顺利成章的得到了双方通信的数据。
本质问题:客户端无法判定发来的秘钥协商报文是不是从合法的服务方发来的!!!!
证书
所以这种方案目前就无解了,别人想怎么搞你,就怎么搞你,所以当人们意识到这种攻击收发会让很多人无所适从,所以我们的网络中就出现了一种非常重要的机构:CA证书机构。
证书是什么
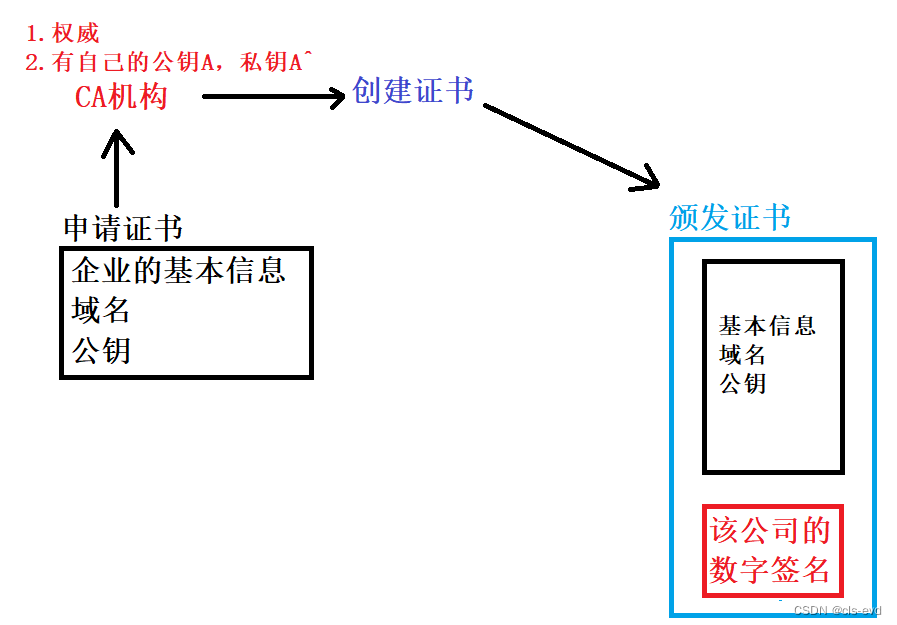
在生活中,我是用人方,你怎么证明你是一个大学生呢,我们就可以通过学校颁发的学位证进行证明,为什么信任各大高校呢,因为各大高校本身就有国家教育部在后面支持,所以只要一个服务商经过权威机构认证,该服务商就是合法的。
比如这个服务端是一个正规的公司的网站,这个服务商首先向CA机构申请证书,申请证书需要提供企业的基本信息,域名,公钥。CA机构拿到你的申请,给你进行创建证书。
CA机构
1.很权威
2.CA机构有自己的公钥A,和私钥A^。
ps:公钥和私钥只是一种算法,任何人都可以有,一点也不值钱。
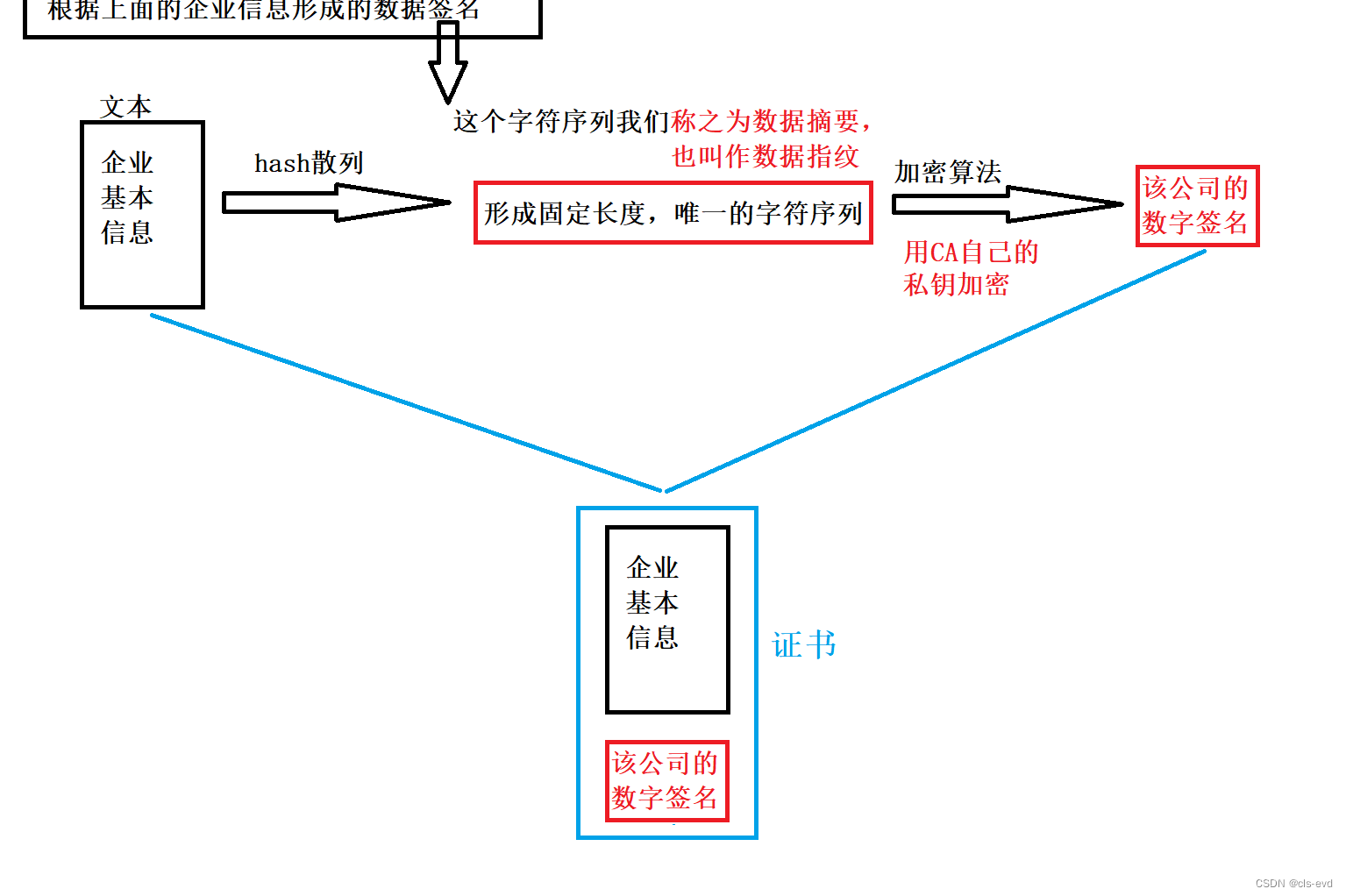
创建证书
创建证书的时候,要有企业的基本信息{域名+公钥(这个公钥与CA机构没关系,是服务器发送给客户端的公钥)},这个企业的基本信息就是一段文本。所以我们根据企业信息形成一个数字签名。
回顾下数字签名形成:这个企业文本经过hash散列形成数据摘要,然后用CA自己的私钥加密,形成该公司的数字签名。 我们把公司基本信息+公司信息的数字签名统称为CA的证书。然后再把这个证书颁发给企业,这个证书里面就包括了公司的基本内容+域名+公钥+公司基本内容的数字签名。
创建证书
CA机构流程
有了证书后,请求该怎么做呢?
客户端发起一个请求,服务端就要把秘钥返回给客户端了,以前就是直接把公钥返回给它,现在就是把证书信息返回给客户端,假如现在中间人就截取了你的证书了,但是现在中间人就不能将服务端的公钥替换成自己的公钥了,因为域名,公钥,基本信息都是明文传送,所有人都能看到,但是人家带了数字签名。当客户端收到证书时,它会把文本内容和签名内容拆出来,然后使用相同的散列算法(这个算法也可以体现在证书上)对该文本进行形成摘要,如果中间人对公钥进行篡改,那么形成的摘要就不是服务端发过来的,而是新的中间人篡改后的摘要, 这样就和解密后的数字签名对不上了。
 数字签名中间人改不了吗?
数字签名中间人改不了吗?
是的!中间人是改不了数字签名的,因为数字签名我们用的是CA机构的私钥进行加密的(当然任何一个人都可以用CA的公钥解密) ,中间人是没有CA机构的私钥的,CA机构的私钥只有CA机构知道,也就是只有CA机构能重新形成对应的数字签名。所以中间人解密出来后,因为没有私钥,也就没办法进行重新生成数字摘要。
如果中间人也是一个合法的服务方呢?
我这个中间人,我也向CA机构申请,CA机构也给我颁发证书,身为中间人的我也就有了合法的证书,我直接把服务端的整个证书报文全部全替换掉,用成中间方的,这样行不行呢?
答案也是不行的,因为证书的基本信息里有一个域名,如果是合法的中间人,你的域名一定和客户端请求的域名一定是不一样的,正如中间人不能改你的域名,不能进行任何篡改,一旦改了就会被侦测出来。换言之,中间人将证书全部替换后,到了客户端,客户端进行秘钥解密的时候,发现一些列都对,但是客户端我原本请求的域名是www.123.com,但现在怎么变成了www.zhongjianren.com了,目标地址发生变化了,我客户端就不相信它了。
所以无论中间人怎么改这个证书,它都改不了!!!
我们认证一个证书是对原始内容进行散列,因为原始内容和散列算法本来就是公开的,我们直接用就可以,关键是对数字摘要解密。所以要求客户端必须知道CA机构的公钥信息。
客户端是如何知道CA机构的公钥信息呢?
1.一般是内置的!相当于你在下载浏览器的时候,这些浏览器本身就已经内置了很多的公钥相关的信息。
2.访问网址的时候,浏览器可能会提示用户进行安装。但这种出现的后果就需要用户自己承担。大部分情况下,我们见到的很多网站,很少提示你让你重新安装证书的。99%情况下直接访问网站,除非它是不合法的。
我们主流的方案是第一种,你的windows操作系统和浏览器都内置了很多的CA机构,这个是软件发布的时候厂商就内置好了,默认下载就有了,涵盖的就是CA机构相关的公钥信息。有了公钥就可以对我们对证书的合法性,是否被篡改做些对应的判定。
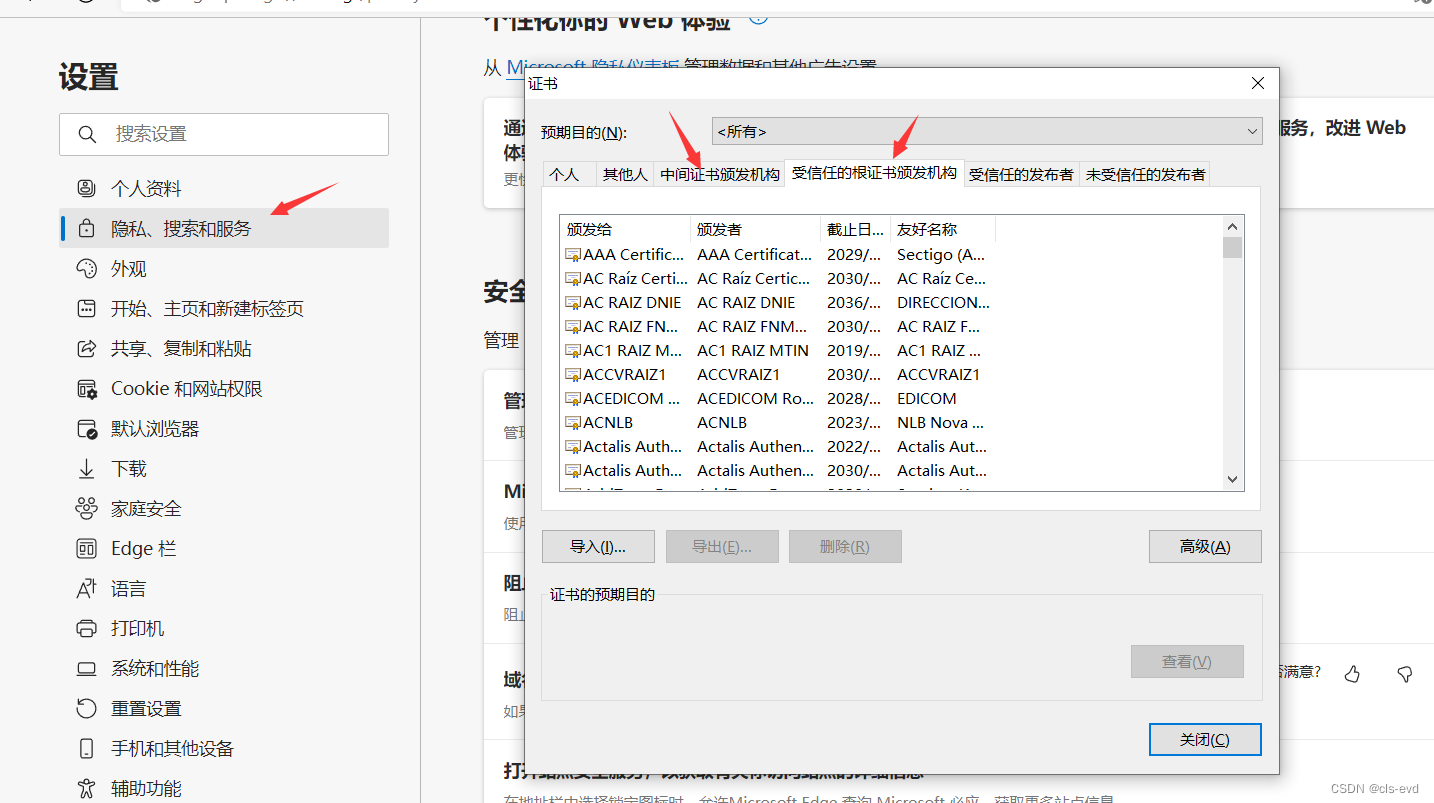
查看证书
受信任的根证书颁发机构,这就是默认设置好的。中间证书颁发机构:就相当于受信任的根证书颁发机构 信任 中间证书颁发机构,因为我们信任根证书机构,只要根证书颁发机构信任的,我们也信任。