金华网站建设seo百度推广在哪里
1、什么是 K3s?
K3s 是一个轻量级的 Kubernetes 发行版,它针对边缘计算、物联网等场景进行了高度优化。K3s 有以下增强功能:
- 打包为单个二进制文件。
- 使用基于 sqlite3 的轻量级存储后端作为默认存储机制。同时支持使用 etcd3、MySQL 和 PostgreSQL 作为存储机制。
- 封装在简单的启动程序中,通过该启动程序处理很多复杂的 TLS 和选项。
- 默认情况下是安全的,对轻量级环境有合理的默认值。
- 添加了简单但功能强大的batteries-included功能,例如:本地存储提供程序,服务负载均衡器,Helm controller 和 Traefik Ingress controller。
- 所有 Kubernetes control-plane 组件的操作都封装在单个二进制文件和进程中,使 K3s 具有自动化和管理包括证书分发在内的复杂集群操作的能力。
- 最大程度减轻了外部依赖性,K3s 仅需要 kernel 和 cgroup 挂载。 K3s 软件包需要的依赖项包括:
containerd
Flannel
CoreDNS
CNI
主机实用程序(iptables、socat 等)
Ingress controller(Traefik)
嵌入式服务负载均衡器(service load balancer)
嵌入式网络策略控制器(network policy controller)
2、为什么叫 K3s?
我们希望安装的 Kubernetes 在内存占用方面只是一半的大小。Kubernetes 是一个 10 个字母的单词,简写为 K8s。所以,有 Kubernetes 一半大的东西就是一个 5 个字母的单词,简写为 K3s。K3s 没有全称,也没有官方的发音。
3、适用场景
K3s 适用于以下场景:
边缘计算-Edge
物联网-IoT
CI
Development
ARM
嵌入 K8s
由于运行 K3s 所需的资源相对较少,所以 K3s 也适用于开发和测试场景。在这些场景中,如果开发或测试人员需要对某些功能进行验证,或对某些问题进行重现,那么使用 K3s 不仅能够缩短启动集群的时间,还能够减少集群需要消耗的资源。与此同时,Rancher 中国团队推出了一款针对 K3s 的效率提升工具:AutoK3s。只需要输入一行命令,即可快速创建 K3s 集群并添加指定数量的 master 节点和 worker 节点。
4、架构详解
K3s server 是运行k3s server命令的机器(裸机或虚拟机),而 K3s worker 节点是运行k3s agent命令的机器。
单节点架构
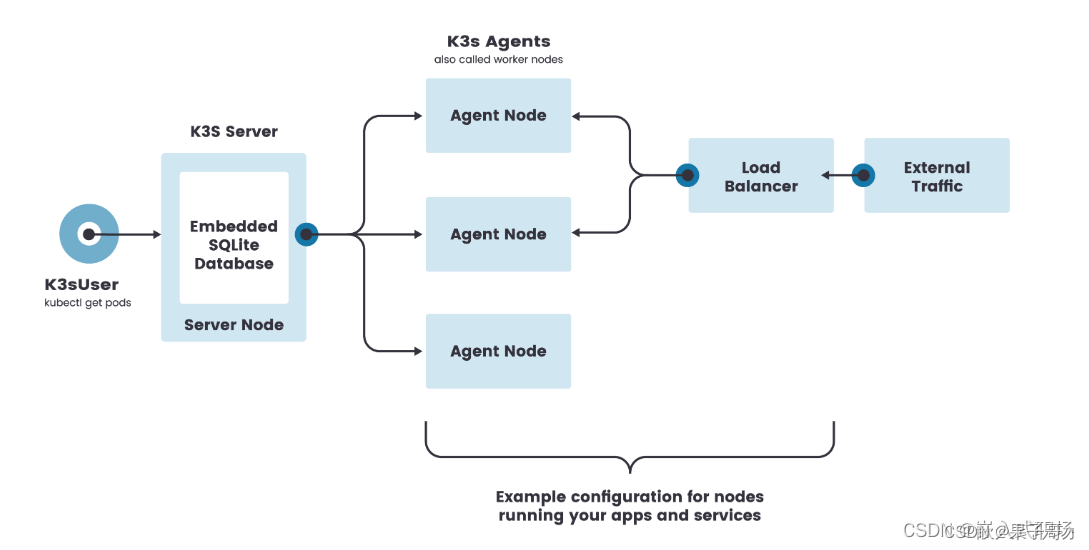
K3s 单节点集群的架构如下图所示,该集群有一个内嵌 SQLite 数据库的单节点 K3s server。
在这种配置中,每个 agent 节点都注册到同一个 server 节点。K3s 用户可以通过调用 server 节点上的 K3s API 来操作 Kubernetes 资源。
单节点k3s server的架构:
高可用架构
虽然单节点 k3s 集群可以满足各种用例,但对于 Kubernetes control-plane 的正常运行至关重要的环境,您可以在高可用配置中运行 K3s。一个高可用 K3s 集群由以下几个部分组成:
- K3s Server 节点:两个或更多的server节点将为 Kubernetes API 提供服务并运行其他 control-plane 服务
- 外部数据库:与单节点 k3s 设置中使用的嵌入式 SQLite 数据存储相反,高可用 K3s 需要挂载一个external database外部数据库作
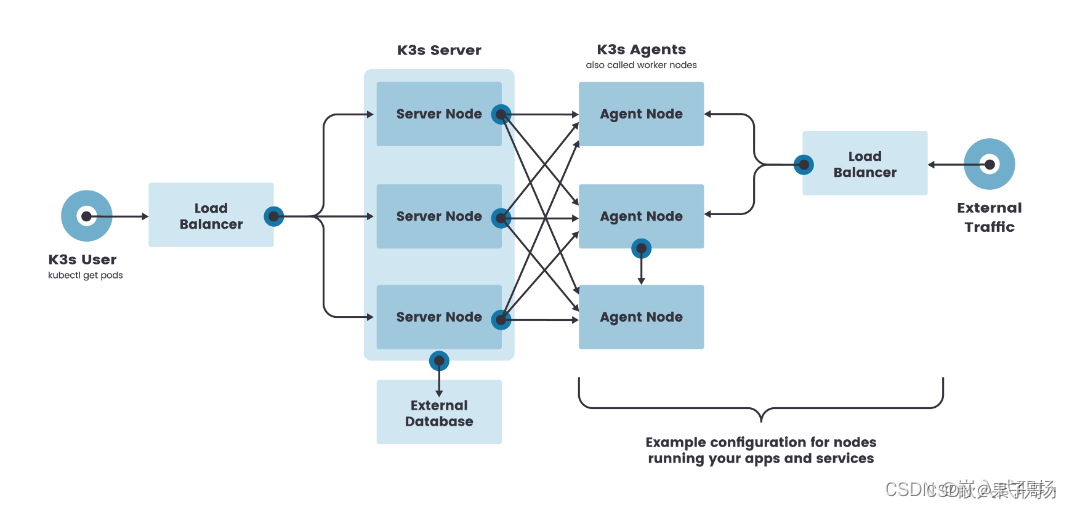
为数据存储的媒介。
固定 agent 节点的注册地址
在高可用 K3s server 配置中,每个节点还必须使用固定的注册地址向 Kubernetes API 注册,注册后,agent 节点直接与其中一个 server 节点建立连接,如下图所示:
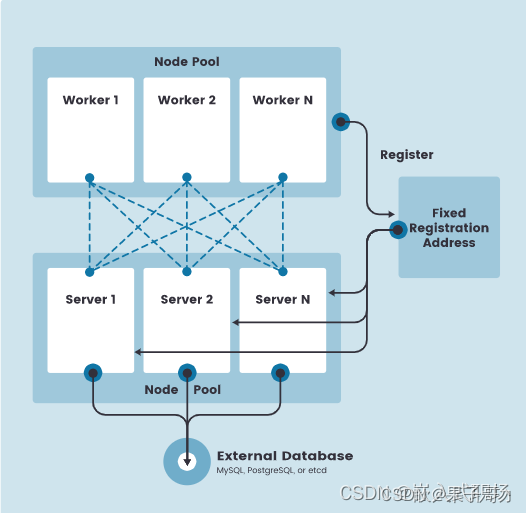
注册 Agent 节点
Agent 节点用k3s agent进程发起的 websocket 连接注册,连接由作为代理进程一部分运行的客户端负载均衡器维护。
Agent 将使用节点集群 secret 以及随机生成的节点密码向 k3s server 注册,密码存储在 /etc/rancher/node/password路径下。K3s server 将把各个节点的密码存储为 Kubernetes secrets,随后的任何尝试都必须使用相同的密码。节点密码秘密存储在kube-system命名空间中,名称使用模板.node-password.k3s。
