用ps做网站网页长春seo顾问
CPU:RK3288
系统:Android 5.1
注:RK3288系统,目前 Android 5.0 Kernel 3.10 SDK 支持 Braodcom,Realtek 等 WiFi BT 模块
各个 WiFi BT 模块已经做到动态兼容,Android 上层不再需要像以前一样进 行特定宏的配置
此文是手动添加AP6212A的例程。
1、在设备树中修改 wifi 芯片为 ap6212a(找到自己对应的dts),修改wifi_chip_type
kernel/arch/arm/boot/dts/marvsmart-rk3288.dts
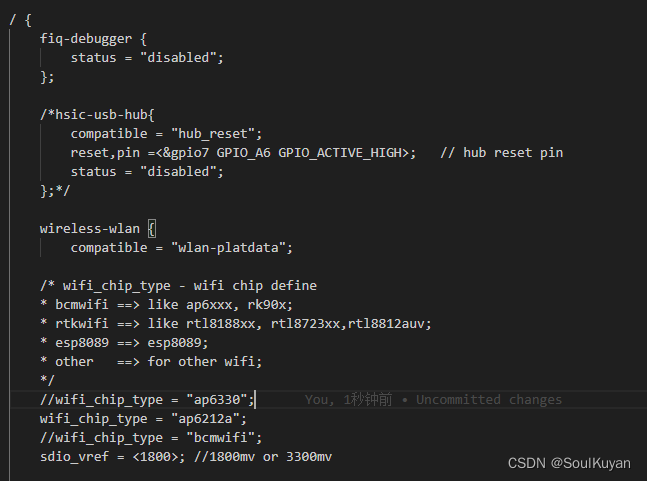
2、在配置文件 defconfig 中屏蔽旧 wifi 芯片,增加新的 wifi 芯片
kernel/arch/arm/configs/marvsmart-rk3288_defconfig
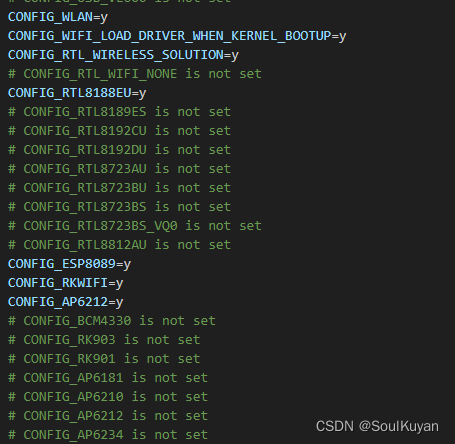
3、在 Kconfig 文件中增加 AP6212 选项。
/kernel/drivers/net/wireless/Kconfig
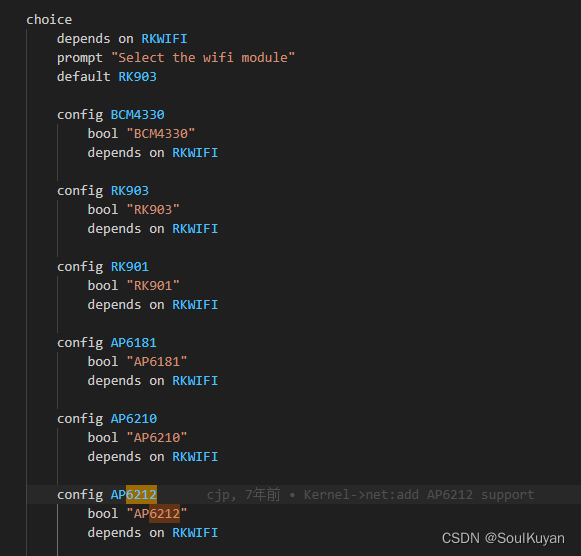
4、此时串口打印中会出现打开文件 fw_bcm43438a1.bin 失败,需要更新 wifi 模块固件。
[ 18.686420] dhdsdio_download_code_file: Open firmware file failed /system/etc/firmware/fw_bcm43438a1.bin [ 18.686430] _dhdsdio_download_firmware: dongle image file download failed
WiFI 固件路径:/external/wlan_loader/firmware
将模块供应商提供的固件文件拷贝到此目录下,然后编译烧录。
external/wlan_loader/firmware/fw_bcm43438a1.bin external/wlan_loader/firmware/fw_bcm43438a1_apsta.bin external/wlan_loader/firmware/fw_bcm43438a1_p2p.bin external/wlan_loader/firmware/nvram_ap6212.txt
编译后,系统会将模块固件拷贝到 out/target/product/rk3288/system/etc//firmware/ 目录下
如果只是调试,可以通过 adb 将固件 push 到 /system/etc//firmware/ 目录下,然后重启。
kernel/include/linux/fkill-wlan.h

wifi 驱动路径:kernel/net/rfkill/rfkill-wlan.c

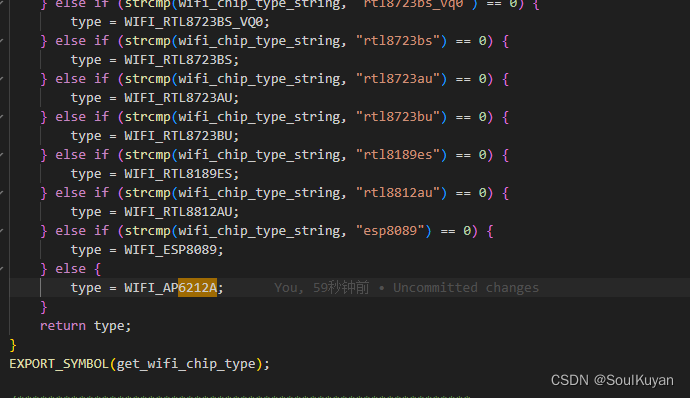
kernel/drivers/net/wireless/rockchip_wlan/rkwifi/rk_wifi_config.c
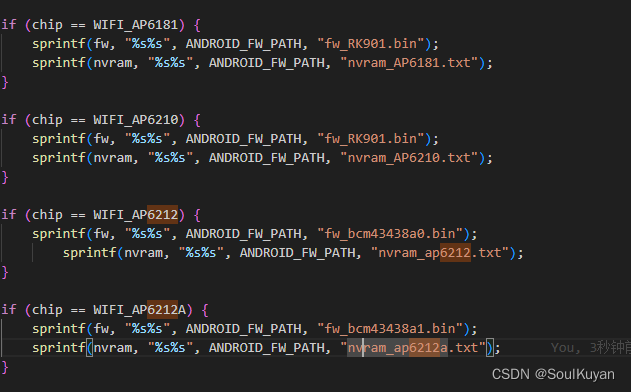
如果器件升级,比如器件为AP6212A,供应商给的文件问 nvram_ap6212a.txt,则需要修改下面文件。(直接用以前的 nvram_ap6212.txt 也可以用,但文件不一样,不清楚)
路径:\kernel\drivers\net\wireless\rockchip_wlan\rkwifi\bcmdhd\dhd_config.c

5、BT 驱动中增添代码,支持 AP6212
BT 驱动路径:kernel/net/rfkill/rfkill-bt.c


到此 AP6212 就可以正常使用了
