南京做网站引流的公司专门发广告的app
前言
桶排序是一种线性时间复杂度的排序算法,它将待排序的数据分到有限数量的桶中,每个桶再进行单独排序,最后将所有桶中的数据按顺序依次取出,即可得到排序结果。
实现原理
-
首先根据待排序数据,确定需要的桶的数量。
-
遍历待排序数据,将每个数据放入对应的桶中。
-
对每个非空的桶进行排序,可以使用快速排序、插入排序等常用的排序算法。
-
将每个桶中的数据依次取出,即可得到排序结果。
代码实现
public static void BucketSort(int[] array){int arrLength = array.Length;if (arrLength <= 1){return;}//确定桶的数量int maxValue = array[0], minValue = array[0];for (int i = 1; i < arrLength; i++){if (array[i] > maxValue)maxValue = array[i];if (array[i] < minValue)minValue = array[i];}int bucketCount = (maxValue - minValue) / arrLength + 1;//创建桶并将数据放入桶中List<List<int>> buckets = new List<List<int>>(bucketCount);for (int i = 0; i < bucketCount; i++){buckets.Add(new List<int>());}for (int i = 0; i < arrLength; i++){int bucketIndex = (array[i] - minValue) / arrLength;buckets[bucketIndex].Add(array[i]);}//对每个非空的桶进行排序int index = 0;for (int i = 0; i < bucketCount; i++){if (buckets[i].Count == 0){continue;}int[] tempArr = buckets[i].ToArray();Array.Sort(tempArr);foreach (int num in tempArr){array[index++] = num;}}}public static void BucketSortRun(){int[] array = { 19, 27, 46, 48, 50, 2, 4, 44, 47, 36, 38, 15, 26, 5, 3, 99, 888};Console.WriteLine("排序前数组:" + string.Join(", ", array));BucketSort(array);Console.WriteLine("排序后数组:" + string.Join(", ", array));}
运行结果
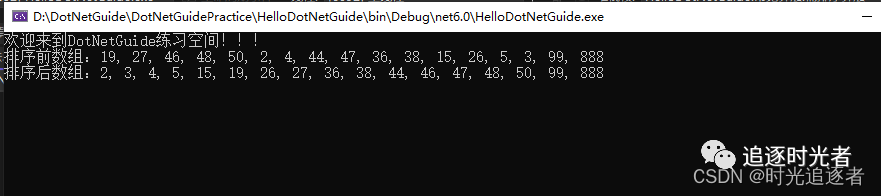
总结
桶排序是一种线性时间复杂度的排序算法,适用于待排序数据分布均匀的情况。它通过将数据分到有限数量的桶中,再对每个桶单独进行排序,最后将桶中的数据按顺序组合起来,得到排序结果。桶排序的时间复杂度为O(n+k),其中n为待排序数据的数量,k为桶的数量。但当数据分布不均匀时,可能会导致某些桶的数据较多,需要进行更多的排序操作,使得效率下降。
