网站建设与管理的总结自己可以做网站吗
目录
索引—index
索引的类型
索引的管理操作
索引的使用
索引—index
使用索引的原因:索引支持在MongoDB中高效地执行查询。如果没有索引,MongoDB必须执行全集合扫描,即扫描集合中的每个文档,以选择与查询语句匹配的文档。这种扫描全集合的查询效率是非常低的,特别在处理大量的数据时,查询可以要花费几十秒甚至几分钟,这对网站的性能是非常致命的。
如果查询存在适当的索引,MongoDB可以使用该索引限制必须检查的文档数。索引是特殊的数据结构,它以易于遍历的形式存储集合数据集的一小部分。索引存储特定字段或─组字段的值,按字段值排序。索引项的排序支持有效的相等匹配和基于范围的查询操作。此外,MongoDB还可以使用索引中的排序返回排序结果。
想了解更多索引的知识推荐看一下官方文档:https://www.mongodb.com/docs/manual/indexes/ 。注意:MongoDB索引使用B树数据结构(确切的说是B-Tree,MySQL是B+Tree)。
索引的类型
索引的类型主要有以下几种,如下:
单字段索引:MongoDB支持在文档的单个字段上创建用户定义的升序/降序索引,称为单字段索引(Single Field Index)。对于单个字段索引和排序操作,索引键的排序顺序(即升序或降序)并不重要,因为MongoDB可以在任何方向上遍历索引。
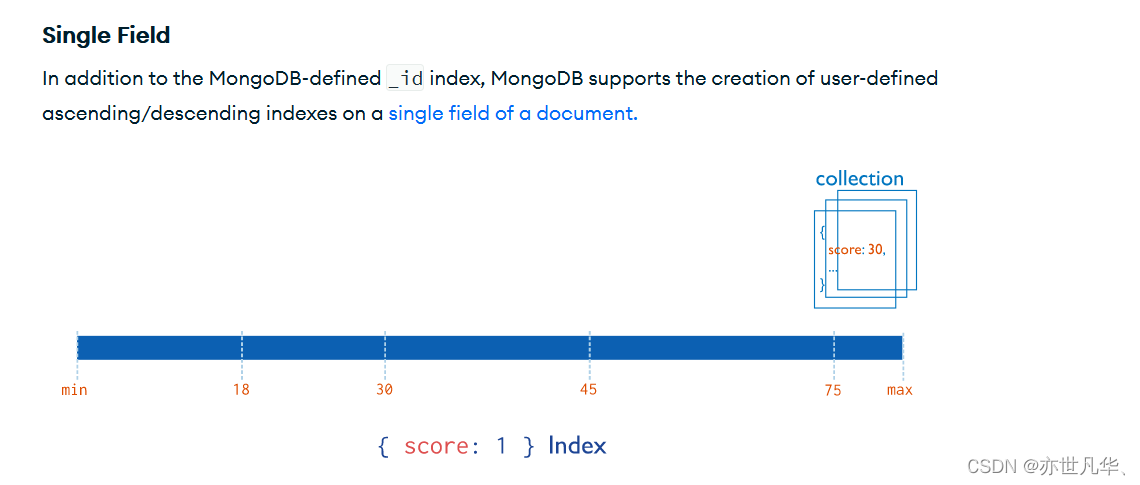
复合索引:MongoDB还支持多个字段的用户定义索引,即复合索引 (Compound lndex)。复合索引中列出的字段顺序具有重要意义。例如,如果复合索引由{ userid: 1, score: -1}组成,则索引首先按userid正序排序,然后在每个userid的值内,再在按score倒序排序。

其他索引:(具体详细内容可参看官方文档)
地理空间索引(Geospatial lndex)
为了支持对地理空间坐标数据的有效查询,MongoDB提供了两种特殊的索引:返回结果时使用平面几何的二维索引和返回结果时使用球面几何的二维球面索引。
文本索引(Text Indexes)
MongoDB提供了一种文本索引类型,支持在集合中搜索字符串内容。这些文本索引不存储特定于语言的停止词(例如“the"、“a"、“or"),而将集合中的词作为词干,只存储根词。
哈希索引(Hashed lndexes)
为了支持基于散列的分片,MongoDB提供了散列索引类型,它对字段值的散列进行索引。这些索引在其范围内的值分布更加随机,但只支持相等匹配,不支持基于范围的查询。
索引的管理操作
对索引的操作大致分为三种:查看、创建、删除。如下:
索引的查看:返回一个集合中所有索引的数组,其基本格式如下:
db.collection.getIndexes()
v:代表当前MongoDB索引引擎的版本
key:自己在哪个字段上加的索引
name:代表索引的名称,默认是 _id_注意:该索引是唯一索引,因此值不能重复,即_id值不能重复的。在分片集群中,通常使用_id作为片键。
索引的创建:在集合上创建索引,其基本格式如下:
db.collection.createIndex(keys,options)| Parameter | Type | Description |
|---|---|---|
| keys | document | 包含字段和值对的文档,其中字段是索引值,值描述该字段的索引类型。 |
| options | document | 可选,包含一组控制索引创建的选项的文档。 |
options更多选择:
unique:建立的索引是否唯一。指定为true创建唯—索引。默认值为false。
name:索引的名称。如果未指定,MongoDB的通过连接索引的字段名和排序顺序生成—个索引名称。
单字段索引的创建:例如对userid字段建立索引,如下:
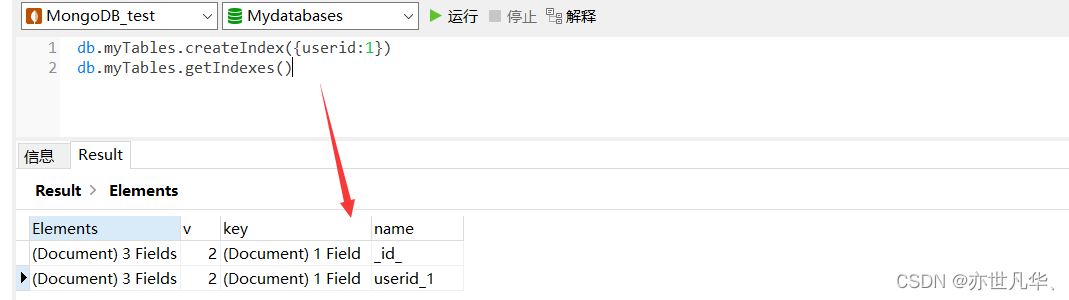
复合索引的创建:例如对userid和other_name通时建立复合(Compound)索引:
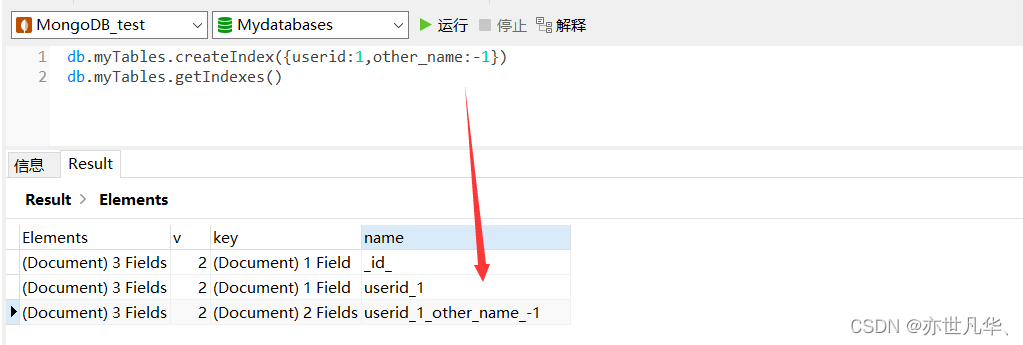
索引的删除:可以移除指定索引或移除所有索引,如下:
指定索引的移除,其基本格式如下:
db.collection.dropIndex(index)index:指定要删除的索引,可以通过索引名称或索引规范文档指定索引。若要删除文本索引,请指定索引名称。
举例,我们想删除 userid 升序的索引,如下:

删除所有索引:其基本语法如下:
db.collection.dropIndexes()除了原本的 _id 不会被干掉,其他创建的索引都会被删除,如下:

索引的使用
索引的使用主要分为以下两种形式:
执行计划:分析查询性能(Analyze Query Performance)通常使用执行计划(解释计划、Explain Plan)来查看查询的情况,如查询耗费的时间、是否基于索引查询等。通常,我们想知道,建立的索引是否有效,效果如何,都需要通过执行计划查看。
其基本语法格式如下:
db.collection.find(query,options).explain(options)为了能够展示更多的信息,这里我采用了 shell 连接操作数据库的方式,来查看更多信息:

// state状态分析如下:
COLLSCAN:全表扫描
IXSCAN:索引扫描
FETCH:根据索引去检索指定document
SHARD_MERGE:将各个分片返回数据进行merge
SORT:表明在内存中进行了排序
LIMIT:使用limit限制返回数
SKIP:使用skip进行跳过
IDHACK:针对_id进行查询
SHARDING_FILTER:通过mongos对分片数据进行查询
COUNT:利用db.coll.explain().count()之类进行count运算
COUNTSCAN:count不使用Index进行count时的stage返回
COUNT_SCAN:count使用了Index进行count时的stage返回
SUBPLA:未使用到索引的$or查询的stage返回
TEXT:使用全文索引进行查询时候的stage返回
PROJECTION:限定返回字段时候stage的返回
对于普通查询,我希望看到stage的组合(查询的时候尽可能用上索引):
Fetch+IDHACK
Fetch+ixscan
Limit+(Fetch+ixscan)
PROJECTION+ixscan
SHARDING_FITER+ixscan
COUNT_SCAN
涵盖查询:当查询条件和查询的投影仅包含索引字段时,MongoDB直接从索引返回结果,而不扫描任何文档或将文档带入内存。这些覆盖的查询可以非常有效。

比如自己将集合中的列表数据增添一个索引为userid,使用涵盖查询如下:

