wordpress建站过程网络营销策略分析论文
目录
一、前言
二、项目简介
1.功能详解
2.主要器件
三、原理图设计
四、PCB硬件设计
1.PCB图
2.PCB板打样焊接图
五、程序设计
六、实验效果
七、资料内容
项目分享
一、前言
项目成品图片: 
哔哩哔哩视频链接:
https://www.bilibili.com/video/BV1oi42117dp/?share_source=copy_web&vd_source=097fdeaf6b6ecfed8a9ff7119c32faf2
(资料分享见文末)
二、项目简介
1.功能详解
基于STM32的家庭环境监测系统。功能如下:
- 温湿度采集:使用DHT11温湿度传感器采集环境温湿度
- 烟雾浓度采集:通过MQ-2烟雾传感器采集环境烟雾浓度
- PM2.5浓度采集:通过粉尘传感器采集环境PM2.5浓度
- 二氧化碳浓度采集:通过CO2气敏传感器检测二氧化碳浓度
- 风扇控制:可自动模式下根据环境温度触发或手动模式下APP开闭
- 加湿器控制:可自动模式下根据环境湿度触发或手动模式下APP开闭
- 窗户:可自动模式下根据PM2.5浓度触发或手动模式下APP开闭
- OLED显示:将检测到的环境数据显示在oled屏幕上。
- 蜂鸣器报警:异常情况下本地蜂鸣器触发报警
- APP功能:使用机智云APP,包括功能有自动模式和手动模式切换,控制并显示风扇、加湿器和窗户状态,查看蜂鸣器报警状态,显示当前环境温湿度、烟雾浓度和PM2,5浓度信息
2.主要器件
- STM32F103C8T6最小系统板
- DHT11温湿度传感器
- OLED显示屏(4针I2C协议)
- WiFi模块(ESP8266-01s)
- MQ-2烟雾浓度传感器
- PM2.5模块
- 28BYJ51步进电机
- 5V风扇模块
- 加湿器模块及驱动板
- 继电器
- 蜂鸣器
- LED灯
三、原理图设计
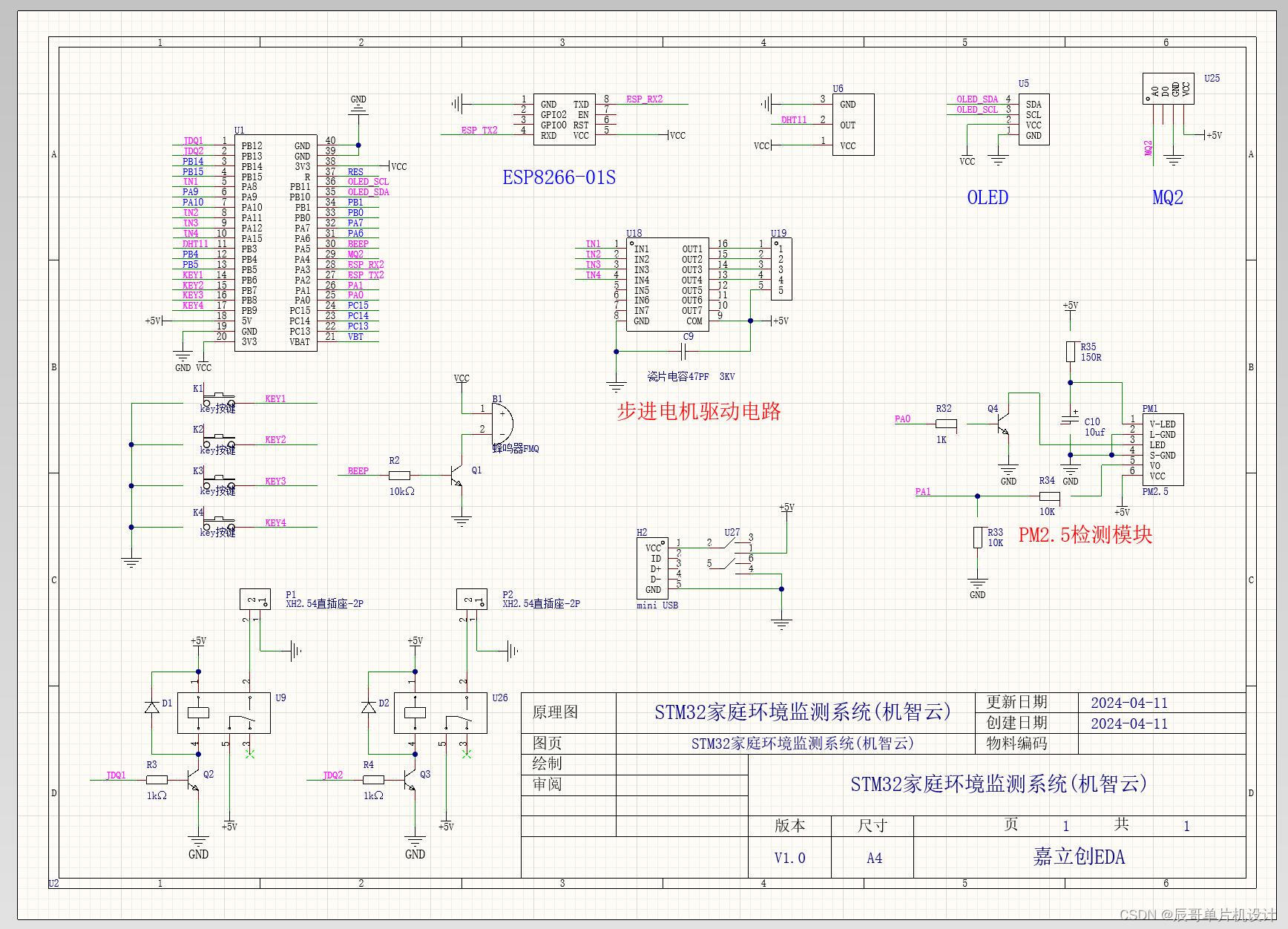
四、PCB硬件设计
1.PCB图
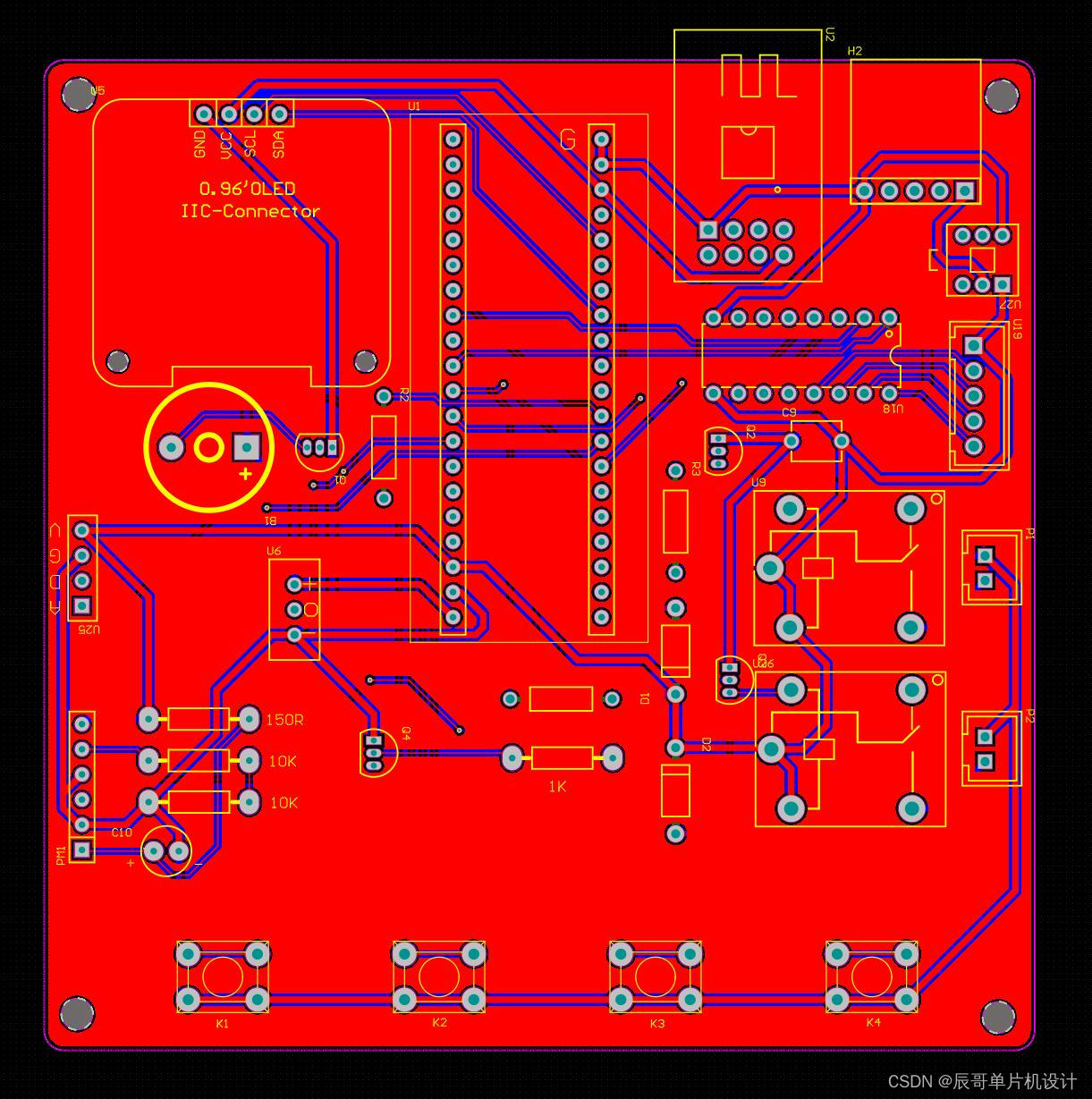
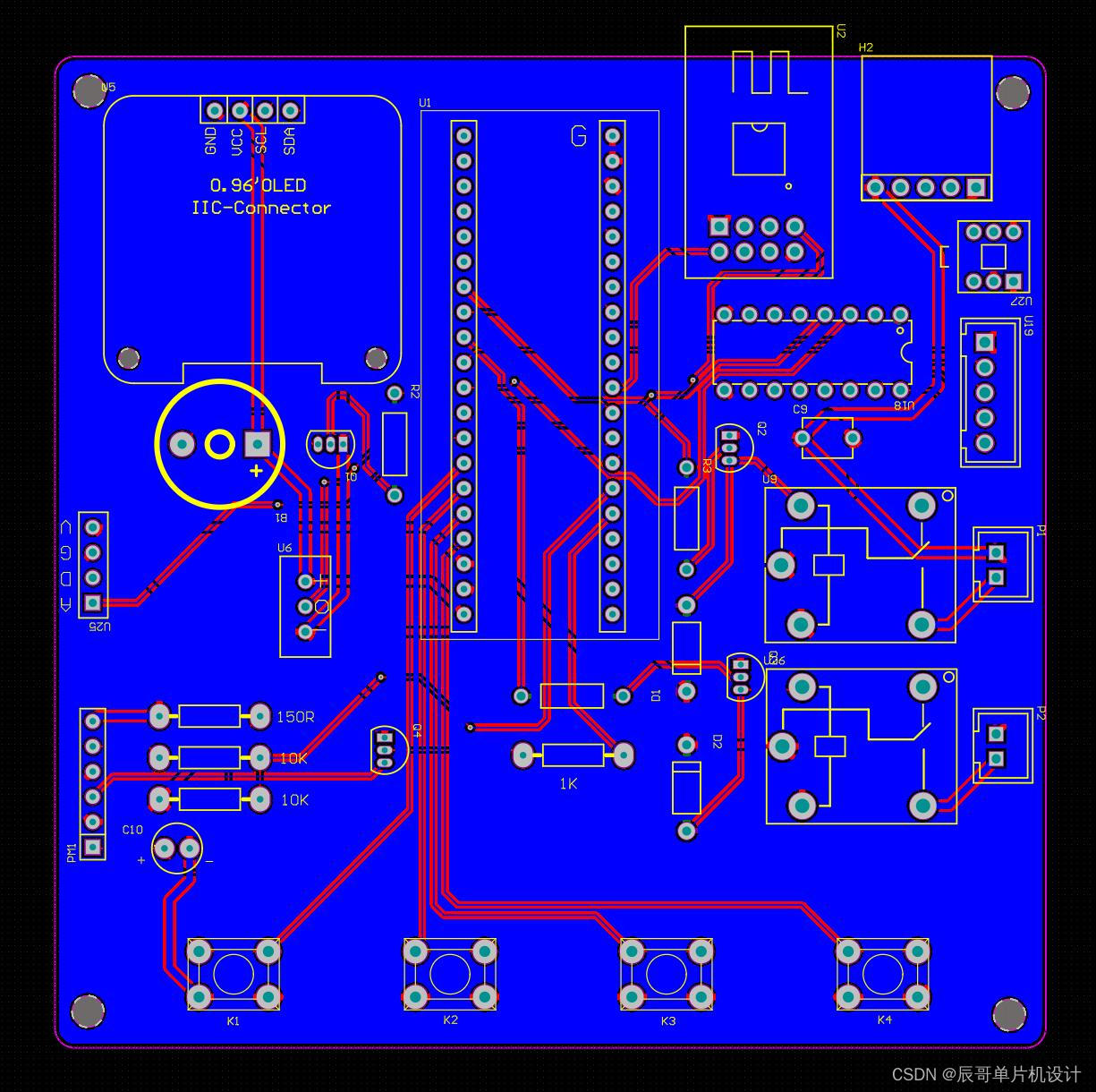
2.PCB板打样焊接图

五、程序设计
int main(void)
{NVIC_PriorityGroupConfig(NVIC_PriorityGroup_2);OLED_Init();ADCX_Init();GP2Y_Init();MQ2_Init();DHT11_UserConfig();MOTOR_UserConfig();Key_Init();Relay_Init();Buzzer_Init();Timer2_Init(9,14398);uart2_init(9600);uart1_init(115200);GENERAL_TIM_Init();userInit(); //完成机智云初始赋值gizwitsInit(); //开辟一个环形缓冲区Delay_ms(500);gizwitsSetMode(WIFI_AIRLINK_MODE);IWDG_Init(); //初始化看门狗while (1){IWDG_ReloadCounter(); //重新加载计数值 喂狗 switch(Menu){case 1: Menu1();//判断步进电机是否需要进行旋转if(Window_Flag_ON == 1){MOTOR_Direction_Angle(1,0,90,1); //顺时针旋转90度MOTOR_STOP();Window_Flag_ON = 0;}if(Window_Flag_OFF == 1){MOTOR_Direction_Angle(0,0,90,1); //逆时针旋转90度MOTOR_STOP();Window_Flag_OFF = 0;}break;case 2: OLED_Clear();Menu2();Menu = 3;//用于判断阈值数据有没有被更改old_Temp_value = Temp_value;old_Humi_value = Humi_value;old_Smog_value = Smog_value;old_PM25_value = PM25_value;break;case 3: //显示传感器阈值OLED_ShowNum(1,13,Temp_value,2);OLED_ShowNum(2,13,Humi_value,2);OLED_ShowNum(3,13,Smog_value,4);OLED_ShowNum(4,13,PM25_value,4);//进行阈值选择if(KeyNum == 1){KeyNum = 0;value_Option_Num++;if(value_Option_Num > 4){value_Option_Num = 1;}}//显示选择标识符“>”OLED_Option(value_Option_Num);//检测阈值数值的调节switch(value_Option_Num){case 1: if(KeyNum == 3){KeyNum = 0;Temp_value++;if(Temp_value >= 100){Temp_value = 1;}}if(KeyNum == 4){KeyNum = 0;Temp_value--;if(Temp_value >= 100){Temp_value = 99;}}break;case 2: if(KeyNum == 3){KeyNum = 0;Humi_value++;if(Humi_value >= 100){Humi_value = 1;}}if(KeyNum == 4){KeyNum = 0;Humi_value--;if(Humi_value >= 100){Humi_value = 99;}}break;case 3: if(KeyNum == 3){KeyNum = 0;Smog_value++;if(Smog_value >= 501){Smog_value = 1;}}if(KeyNum == 4){KeyNum = 0;Smog_value--;if(Smog_value >= 5001){Smog_value = 500;}}break;case 4: if(KeyNum == 3){KeyNum = 0;PM25_value++;if(PM25_value >= 501){PM25_value = 1;}}if(KeyNum == 4){KeyNum = 0;PM25_value--;if(PM25_value >= 501){PM25_value = 500;} }break;}//退出阈值设置界面if(KeyNum == 2){KeyNum = 0;//当阈值数据被更改后,才会写入FLASH中if((old_Temp_value != Temp_value) || (old_Humi_value != Humi_value) || (old_Smog_value != Smog_value) || (old_PM25_value != PM25_value)){//写入传感器阈值数据FLASH_W(FLASH_START_ADDR,Temp_value,Humi_value,Smog_value,PM25_value); }Menu = 1; //回到主菜单OLED_Clear(); //清屏}break; }userHandle(); //更新机智云数据点变量存储的值gizwitsHandle((dataPoint_t *)¤tDataPoint); //数据上传至机智云 }
}六、实验效果


七、资料内容

