房地产网站建设方案seo是啥软件
笔者使用的ESXI7.0 Update 3 抱着试试的态度想安装一下苹果的MacOS系统
主要步骤有2个
1.解锁unlocker虚拟机系统
2.安装苹果MacOS系统

需要下载的文件
unlocker
这一步是最耗时间的,要找到匹配自己系统的unlocker文件。
https://github.com/THDCOM/ESXiUnlocker/releases/
下载esxi-unlocker-3.0.3.tgz文件 , 笔者使用 3.0.3安装失败,于是又试了3.0.1 https://download.csdn.net/download/RGBBB/72129961 最终unlocker成功。
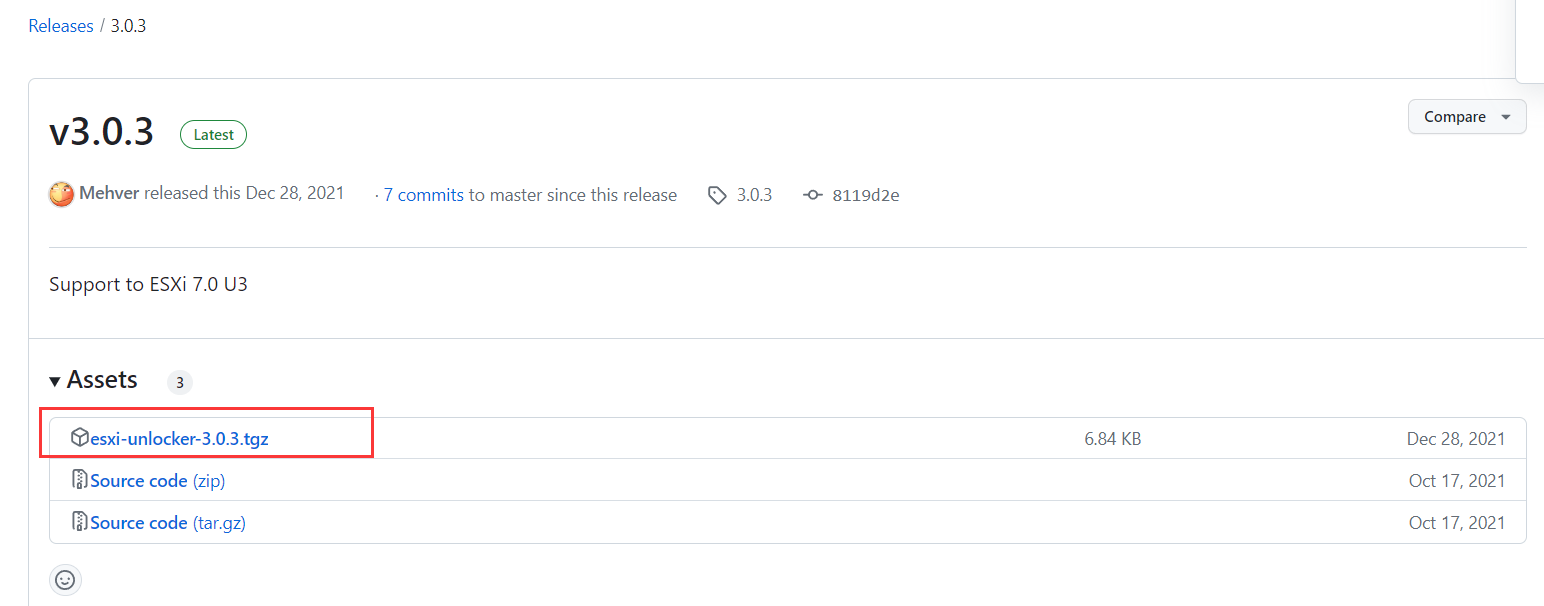
3.0.1链接(笔者使用成功):https://pan.baidu.com/s/1wKyqlBA34gXufybJir36Rw?pwd=kidi
提取码:kidi
3.0.3备用下载链接:https://pan.baidu.com/s/1DtbtalyqlqIwKAyJ7W2r2Q?pwd=6gw3
提取码:6gw3
下载苹果系统
苹果macOS Monterey 12.7 (21G816) MH 下载
链接: https://pan.baidu.com/s/19Gsger55r9wVt79lO9qRnA?pwd=kebq
提取码: kebq
下载完成之后上传到ESXI的目录中
解锁虚拟机
1.上传文件 unlocker的压缩文件
2.启动SSH
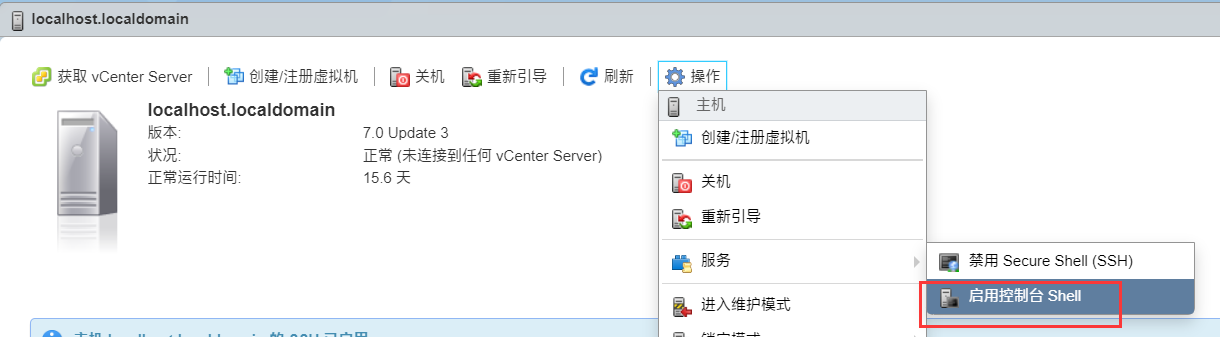
3.进入文件夹,安装unlocker
$ df -h
Filesystem Size Used Available Use% Mounted on
VMFS-6 1.9T 1.0T 869.2G 54% /vmfs/volumes/datastore1
VMFS-6 1.9T 483.6G 1.4T 25% /vmfs/volumes/Data2T$ cd /vmfs/volumes/Data2T/OS解压:
$ tar -zxvf esxi-unlocker-3.0.3.tgz 安装unlocker并重启:
$ ./esxi-install.sh
VMware Unlocker 3.0
===============================
Copyright: Dave Parsons 2011-18
Powered by sysin.org
Installing unlocker.tgz
Acquiring lock /tmp/bootbank.lck
Copying unlocker.tgz to /bootbank/unlocker.tgz
Editing /bootbank/boot.cfg to add module unlocker.tgz
Success - please now restart the server!#重启
reboot
4.检查补丁是否成功
重启成功之后
cd /vmfs/volumes/Data2T/OS/
./esxi-smctest.sh
苹果macOS Monterey
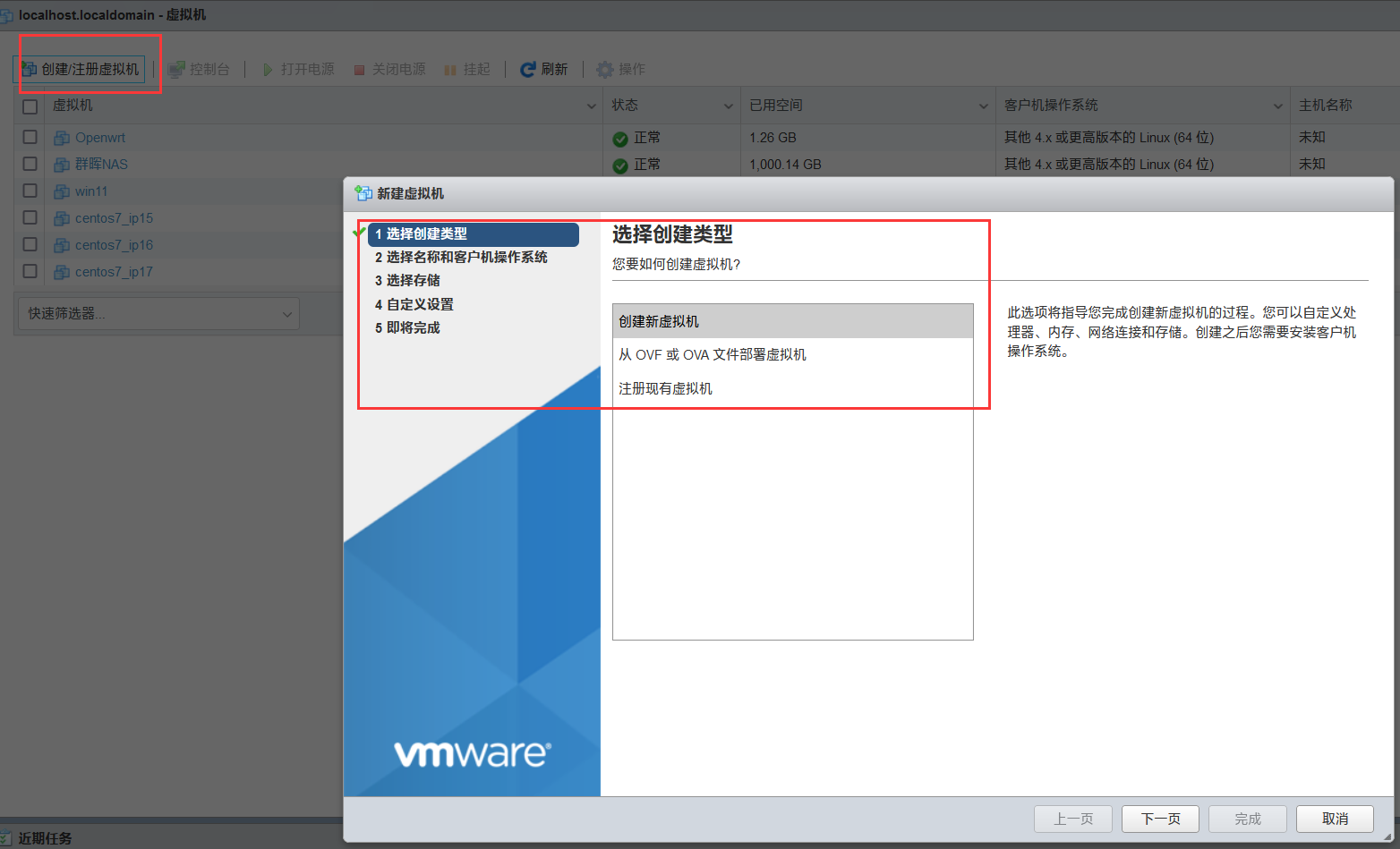
1.创建虚拟机
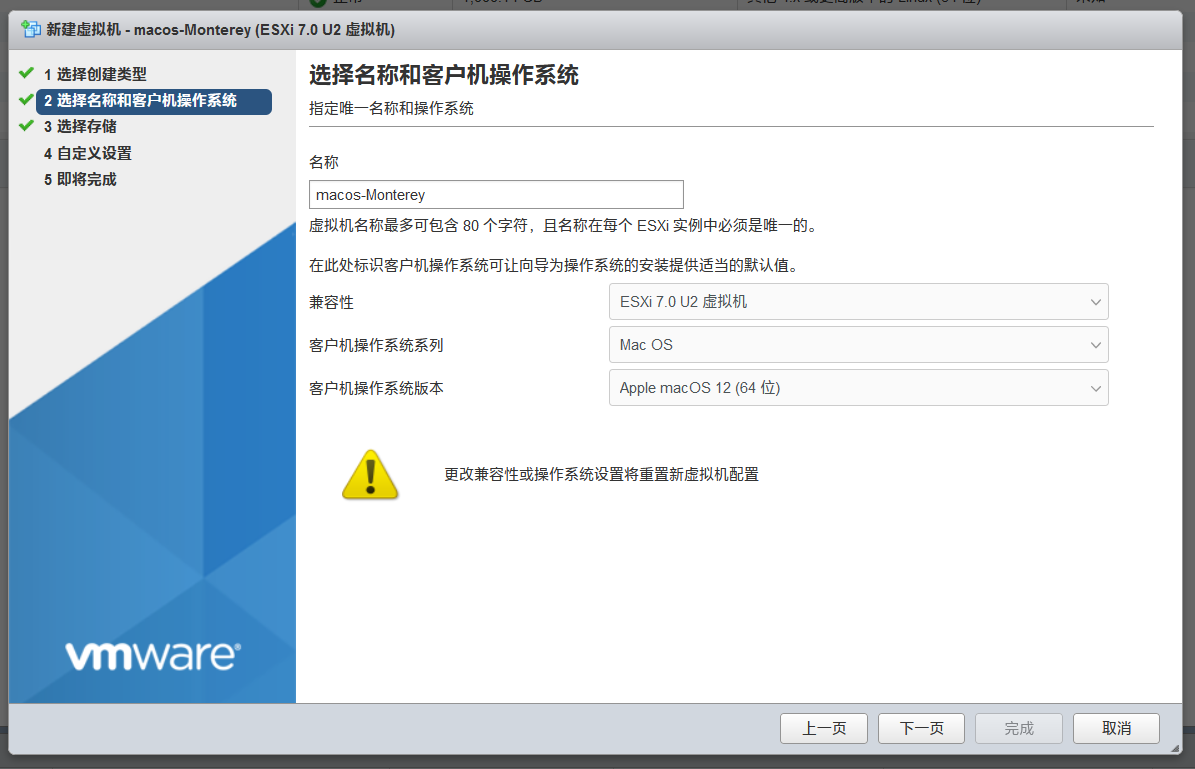
2.选择名称和客户机操作系统
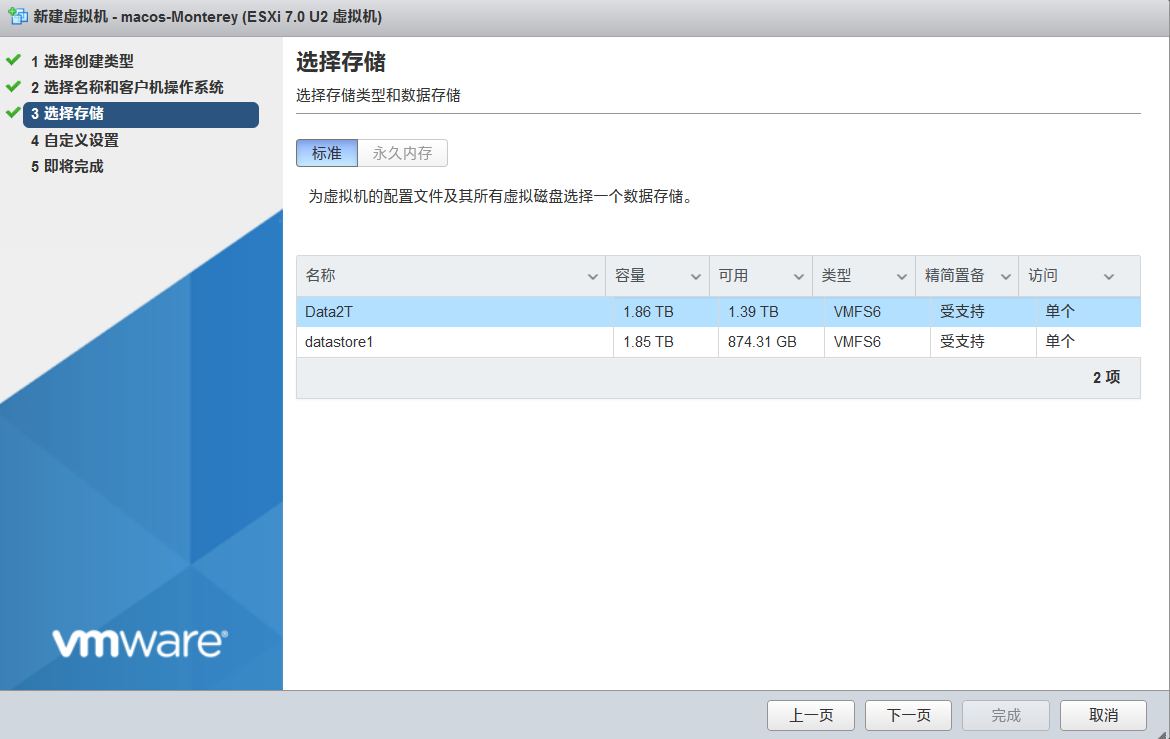
3.选择存储
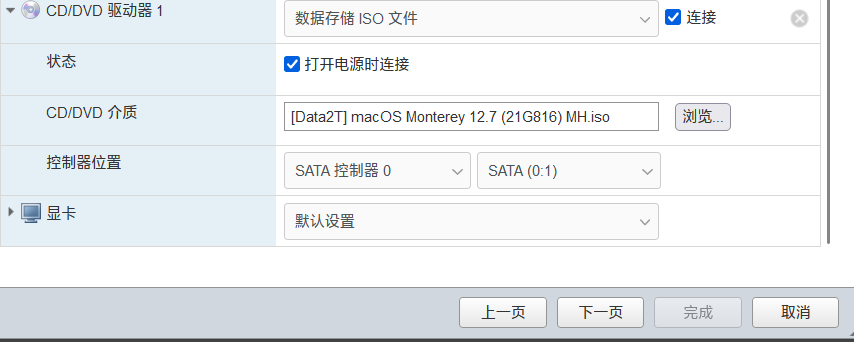
4.自定义设置
cpu和内存硬盘根据实际需要设置

最主要设置CD/DVD选择 MAC系统的文件
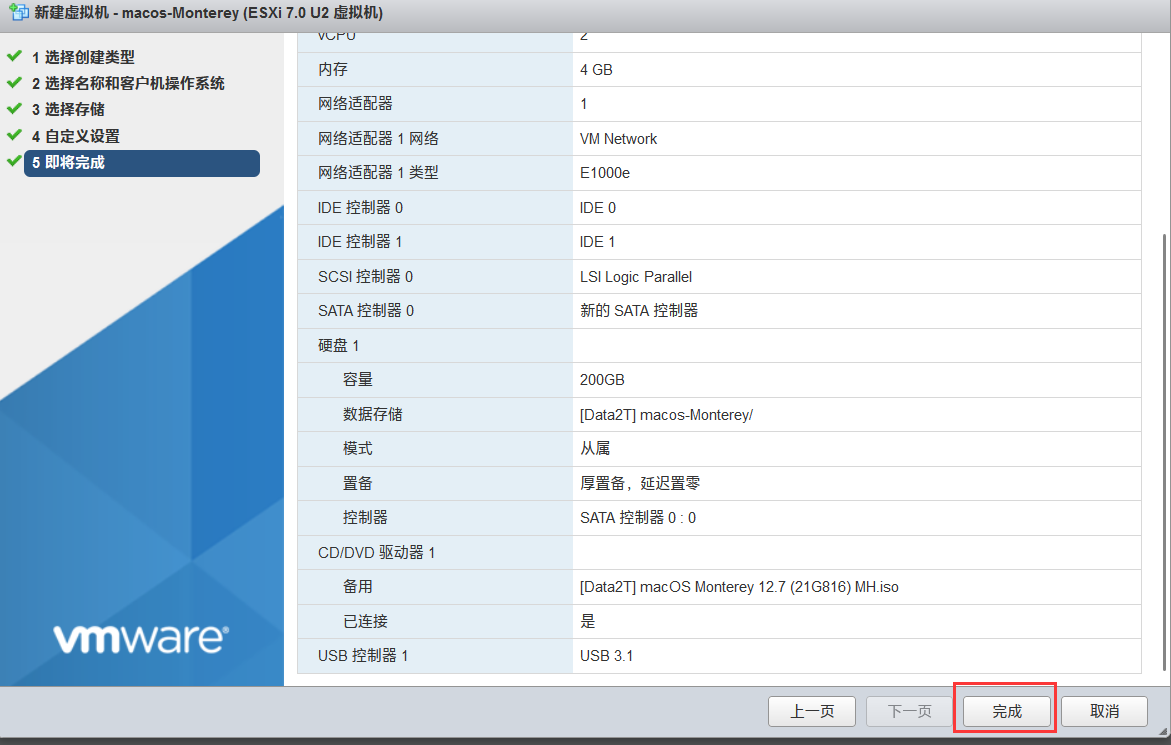
5.即将完成
6.启动macos电源
7.选择语言
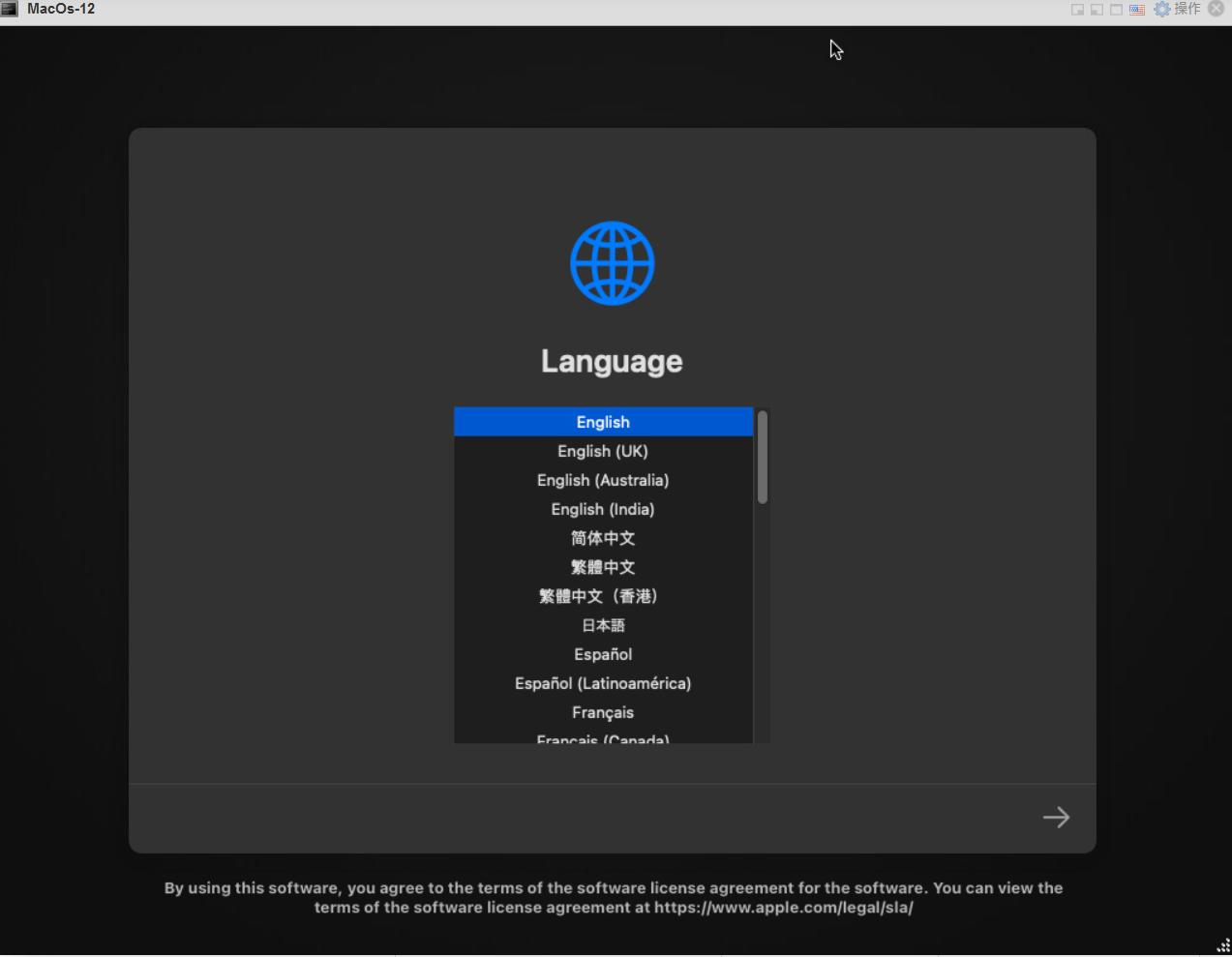
8.磁盘工具
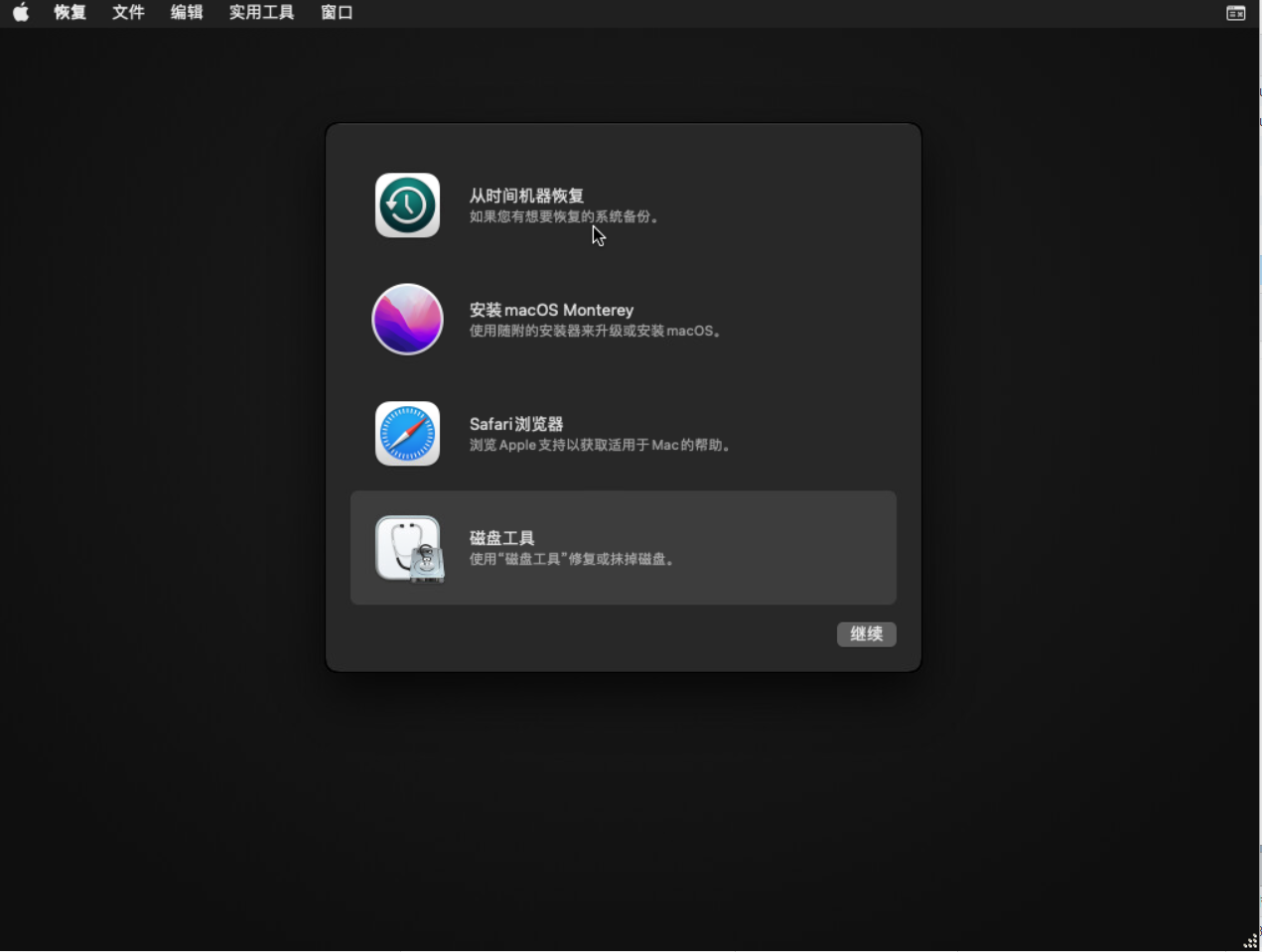
9.格式化磁盘
选择抹掉
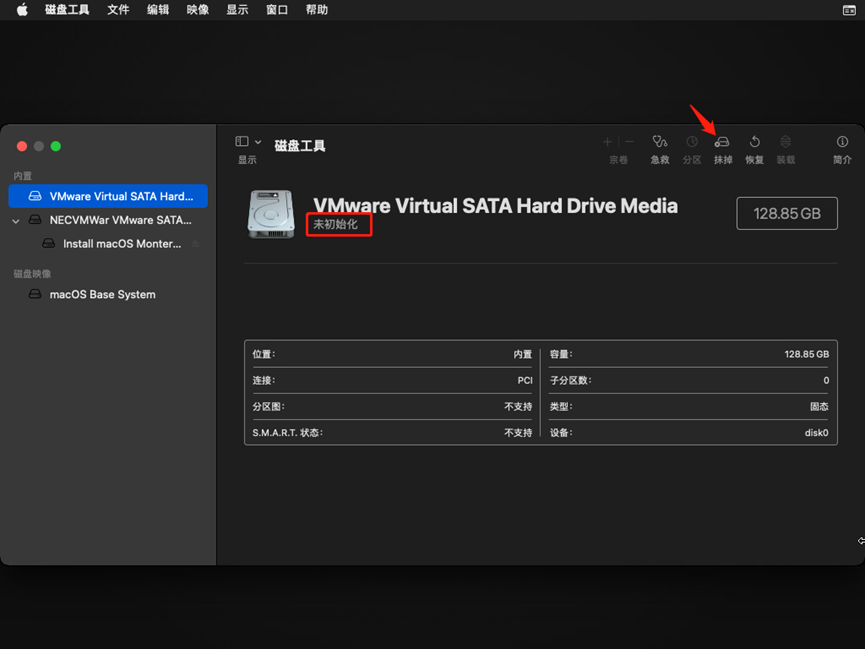
磁盘名称

10.安装macOS

11.点击继续
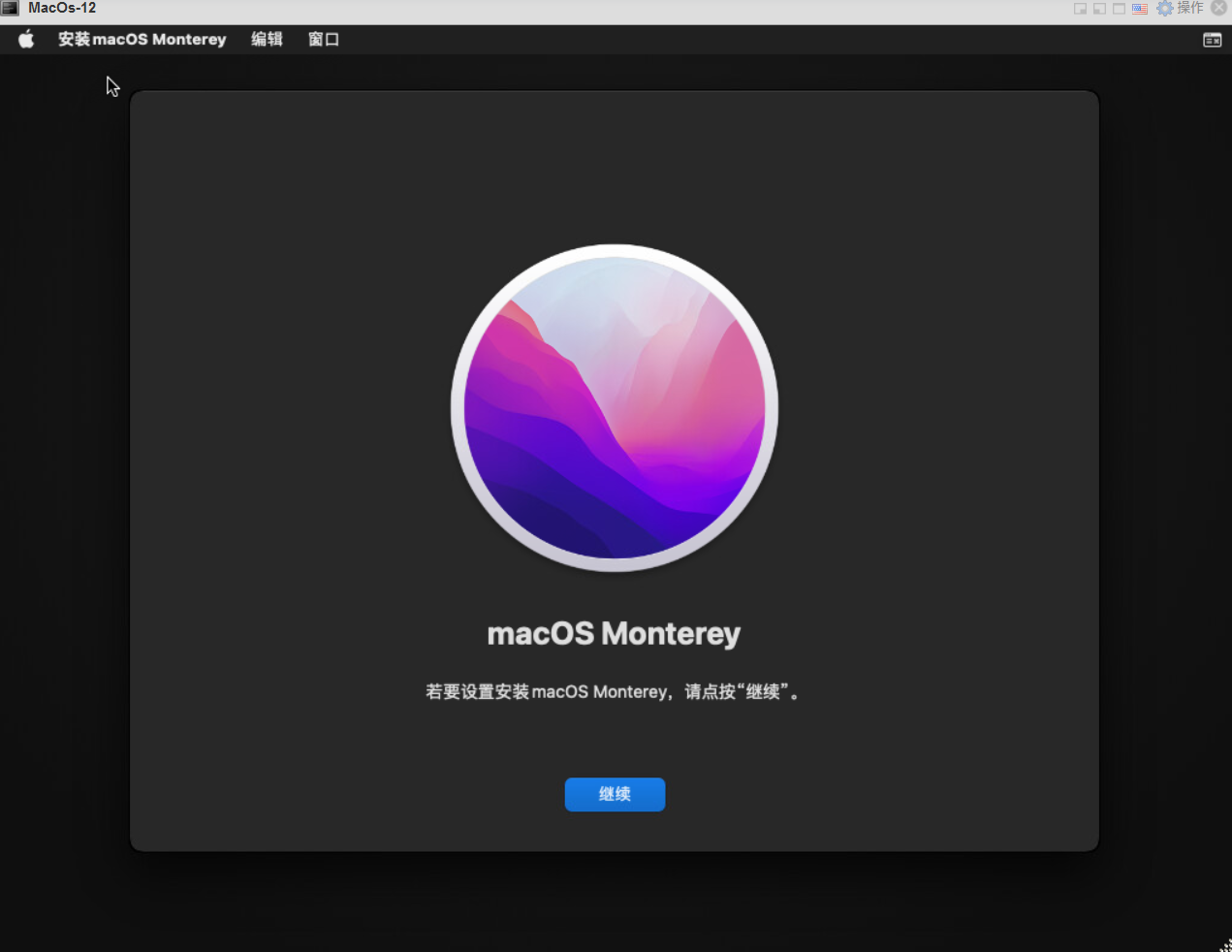
12.同意软件政策
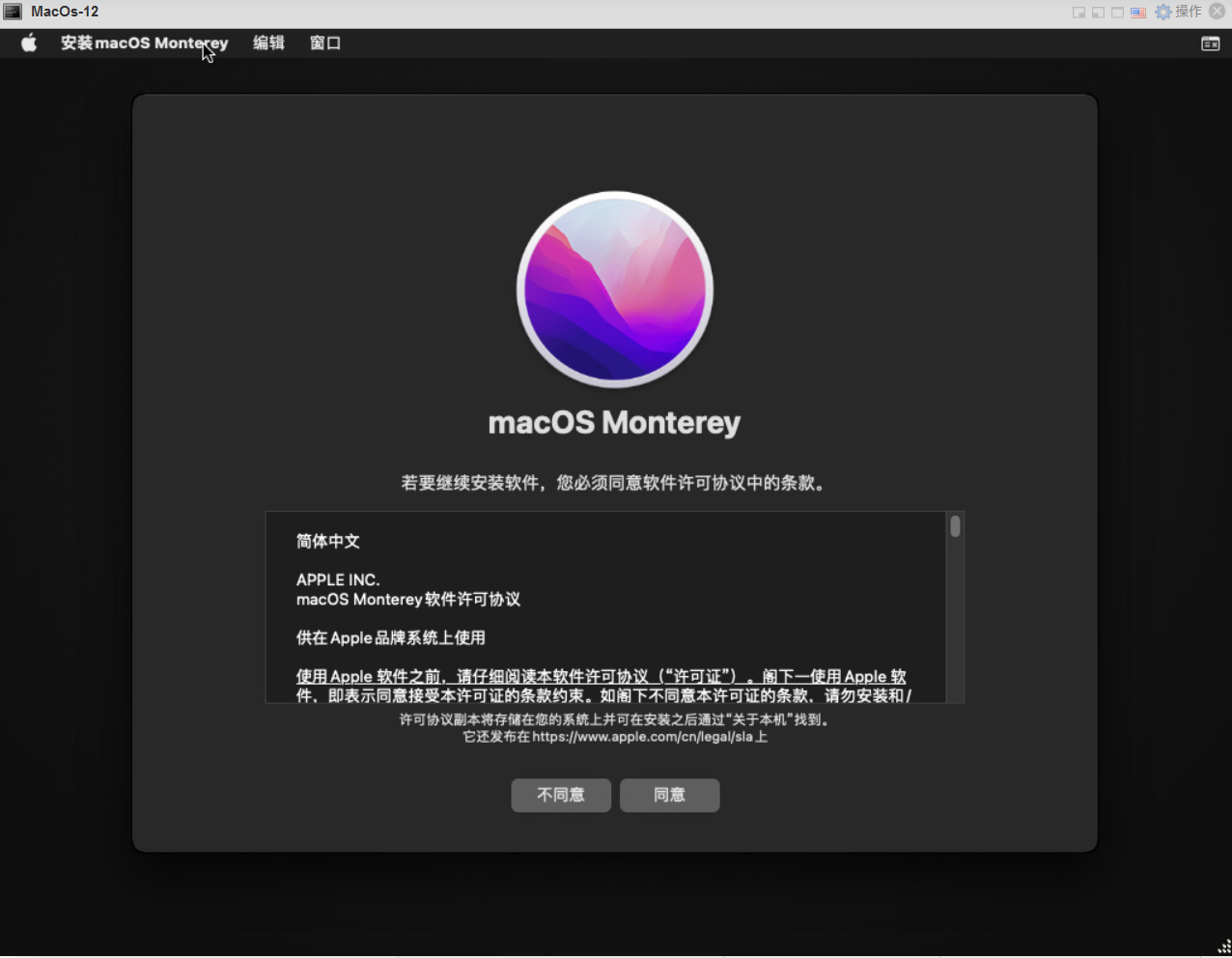
13.安装系统到磁盘

14.安装系统中
等待

15.选择国家和地区

16.语言与输入法

17.辅助功能
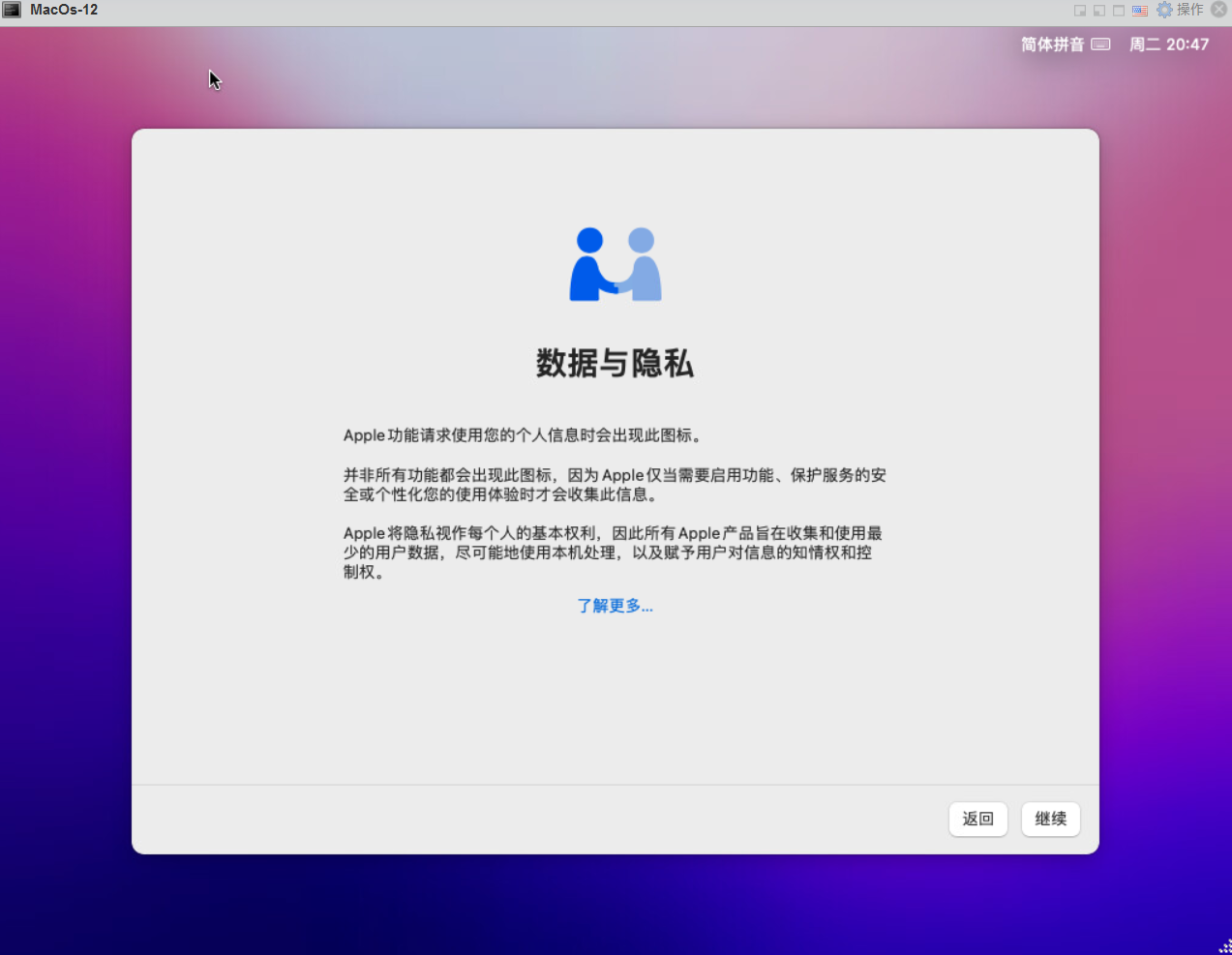
18.数据与隐私
19.迁移助理

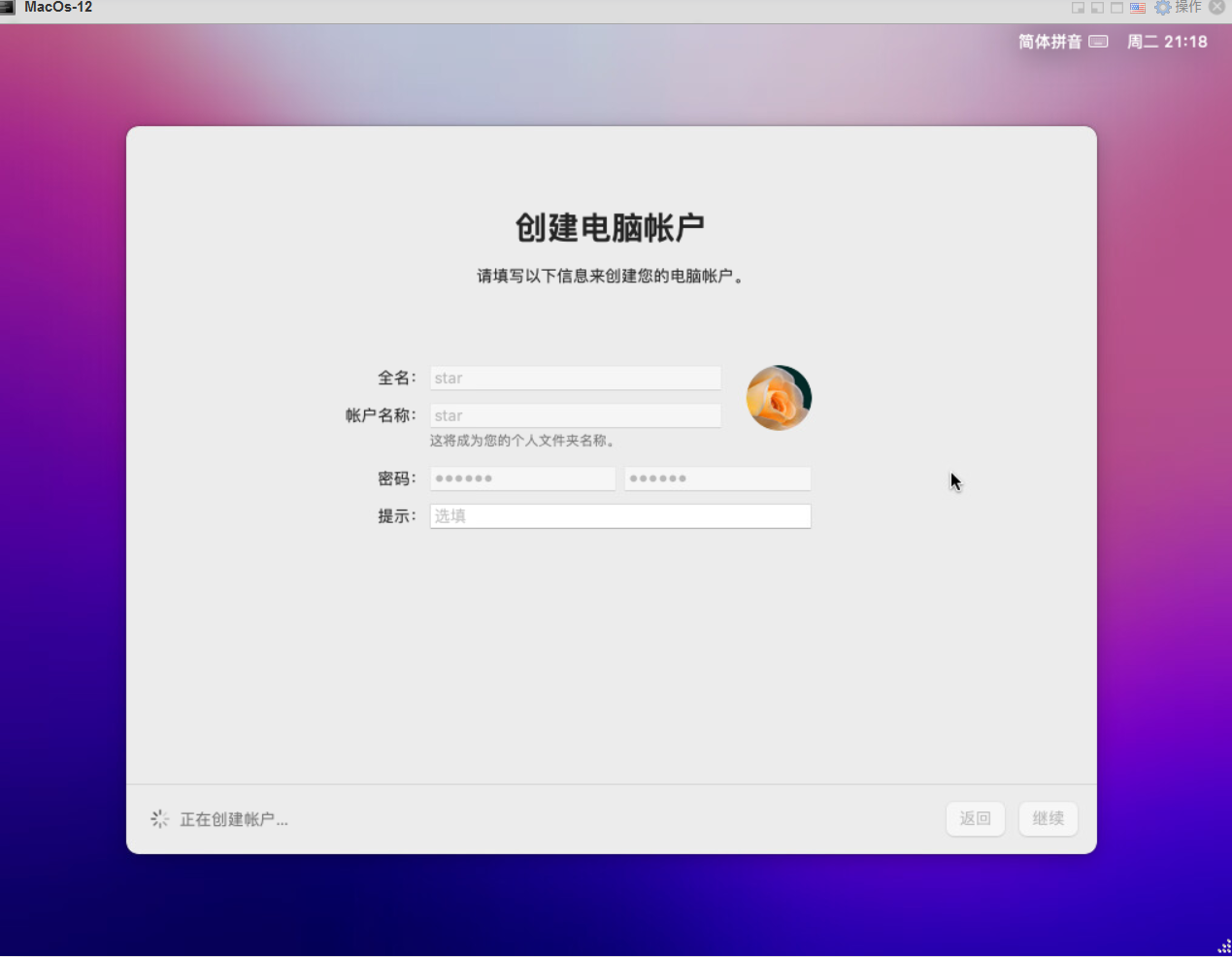
20.创建账户
21.安装成功
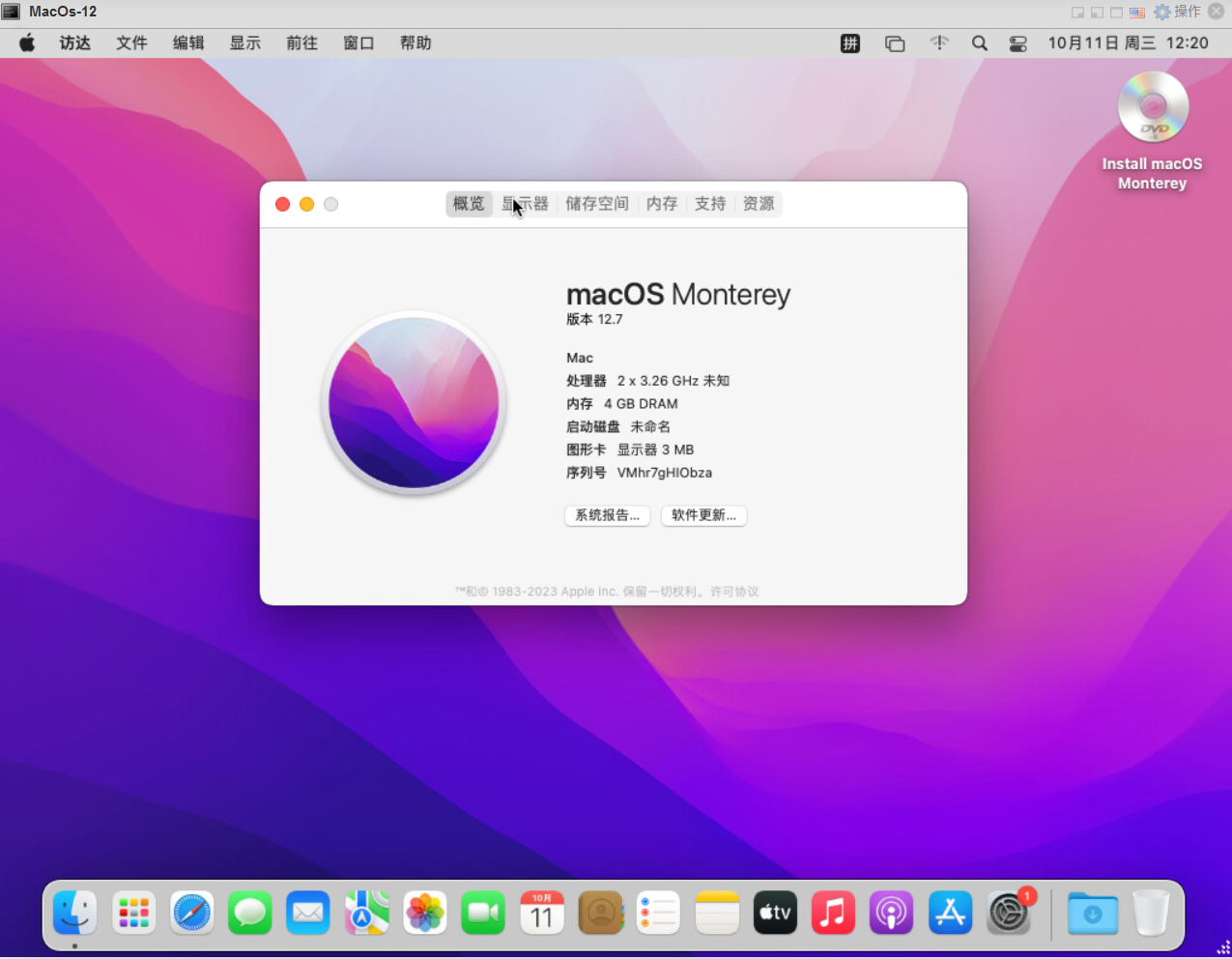
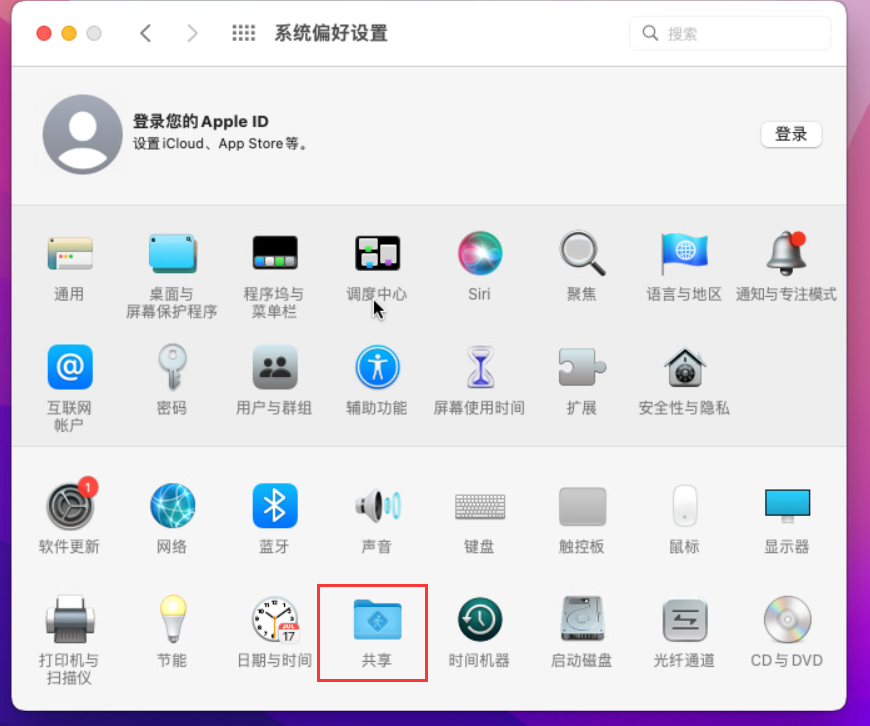
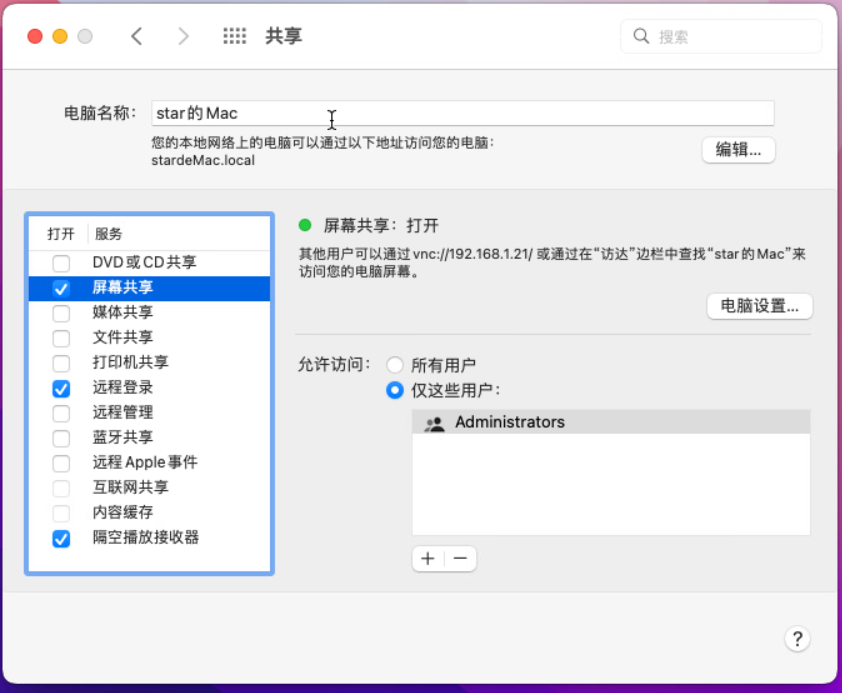
macOS开启屏幕共享

下载VNC viewer 软件
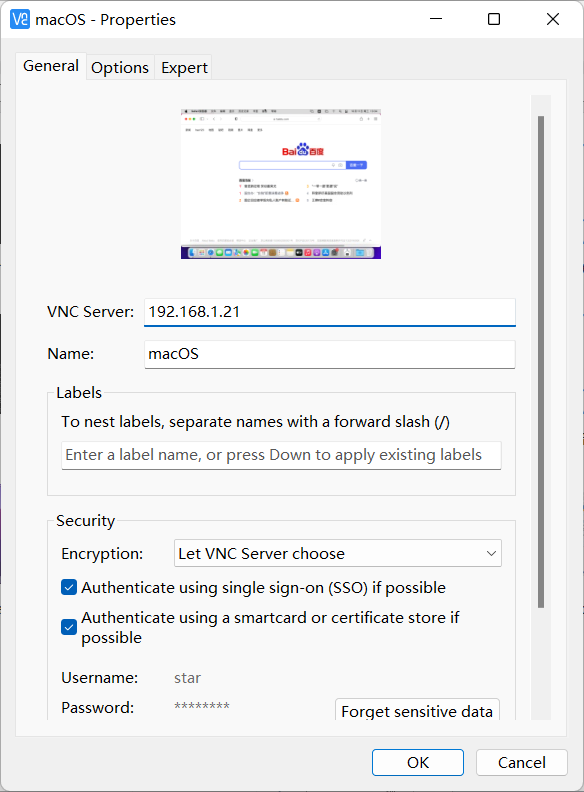

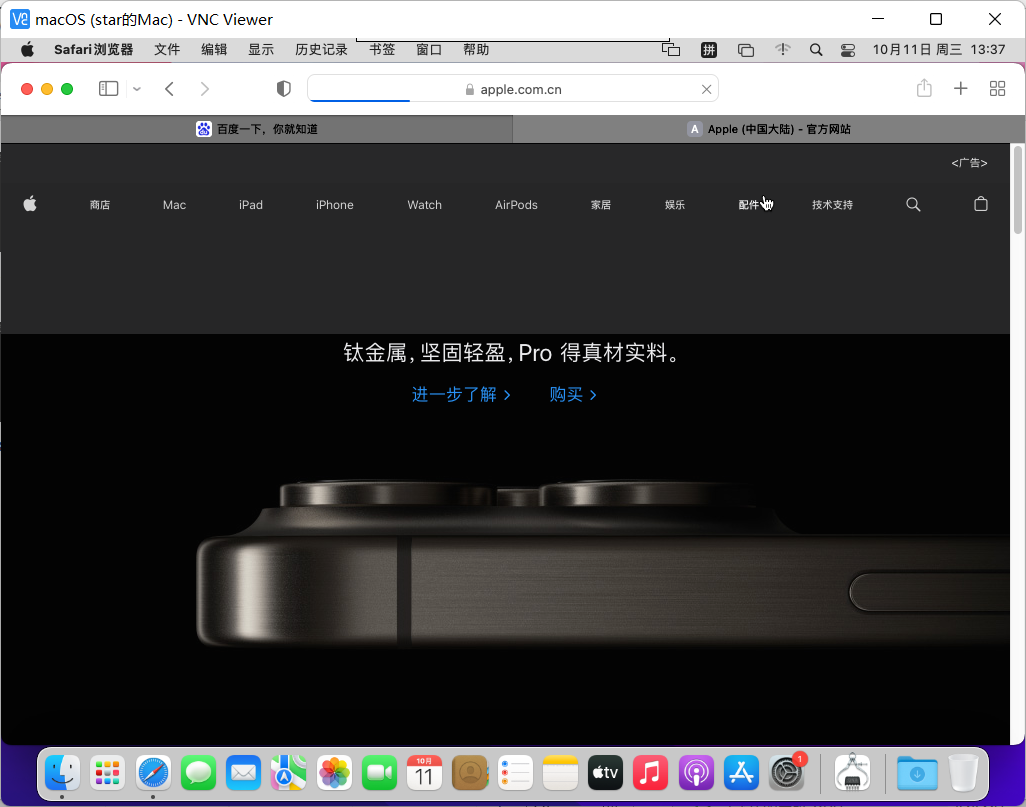
至此,这是就是用esxi7.0安装苹果MacOS系统的教程了。
在Win11上用vmware连接Esxi
文件—>连接服务器
输入Esxi的ip地址,用户名和密码。
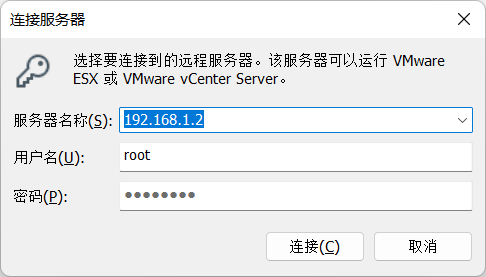
就可以不用浏览器管理Esxi。
安装VMware Tools
无法修改分辨率的问题,需要安装VMware Tools
下载darwin.iso:http://www.downza.cn/soft/341609.html
备用下载链接:https://pan.baidu.com/s/1Ef3RnlmQbZ5TJlFltQ-ajA?pwd=daab
提取码:daab
1.将darwin.iso文件上传EXSI中
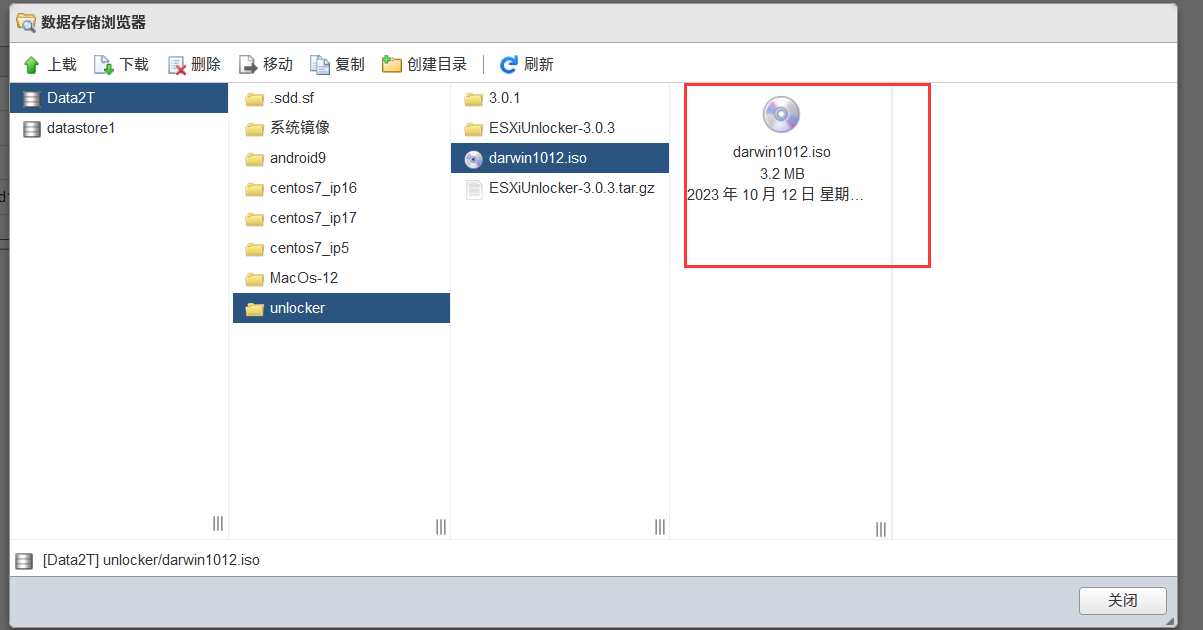
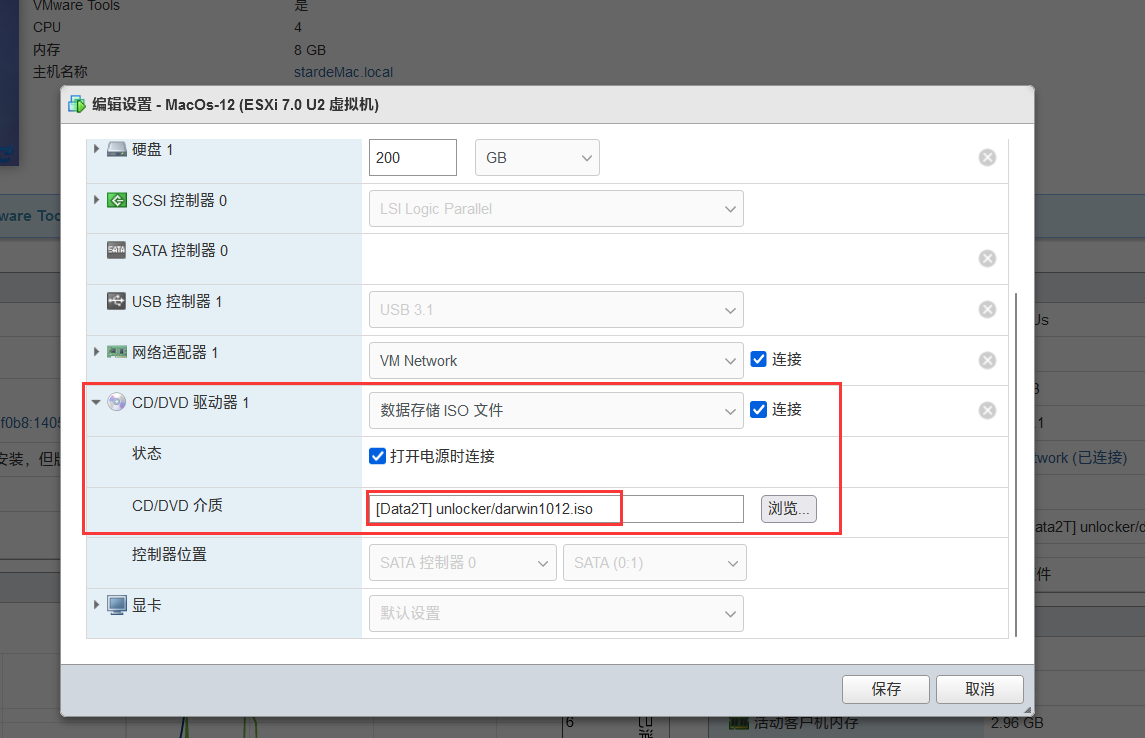
2.修改苹果系统的配置
在CD/DVD介质中设置路径
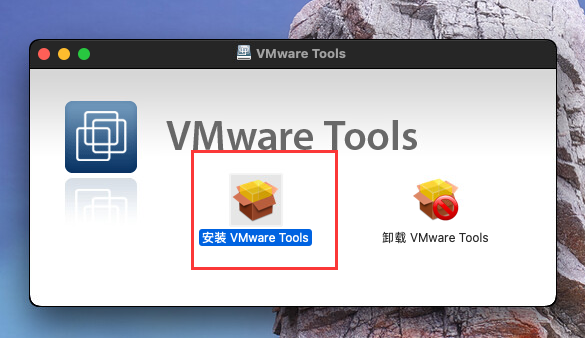
3.苹果系统开机
桌面就出现了VMware Tools

4.打开安装
5.安装重启之后就可以缩放
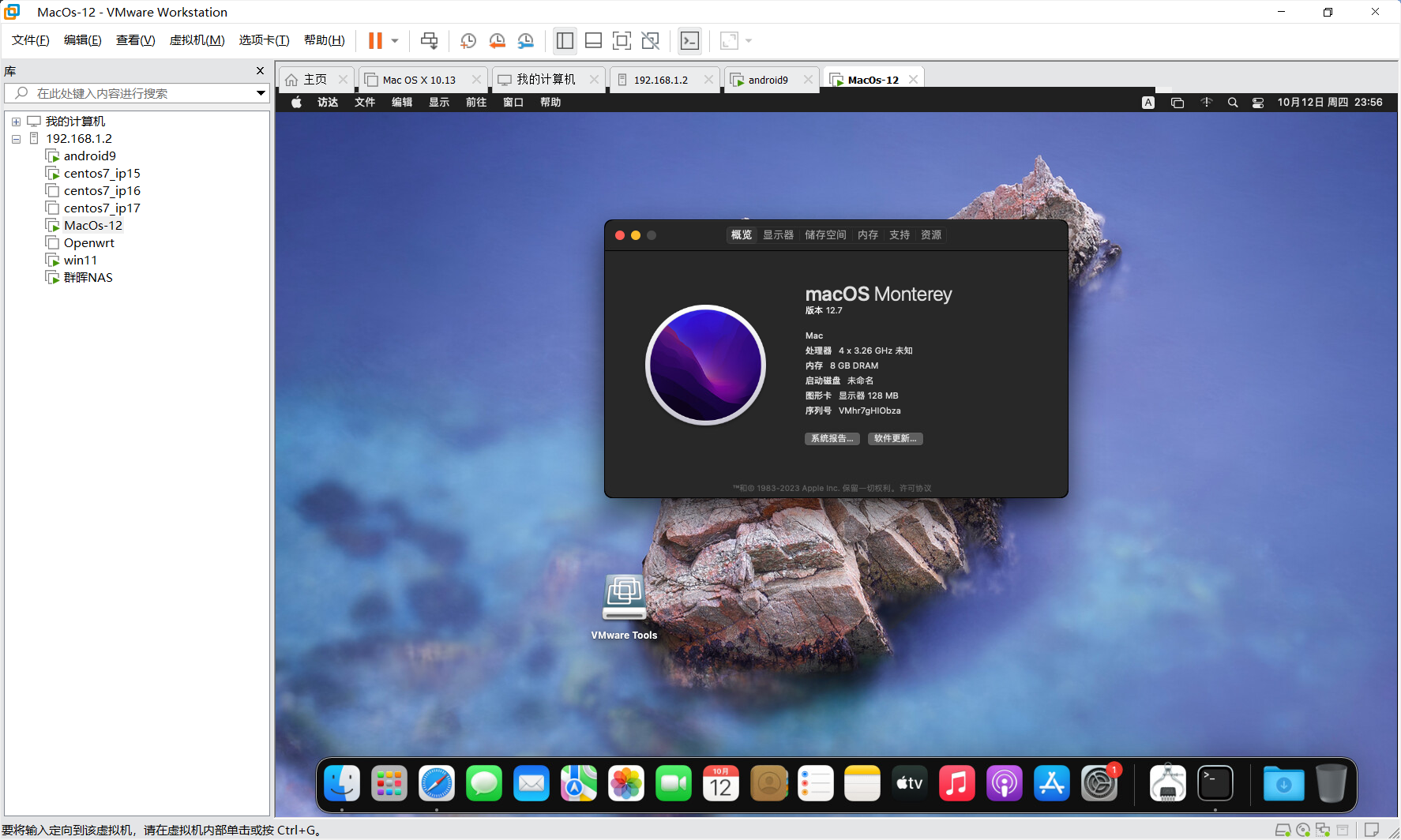
再设置一下快照,就可以随便造了。
手残升级 sonoma14.0
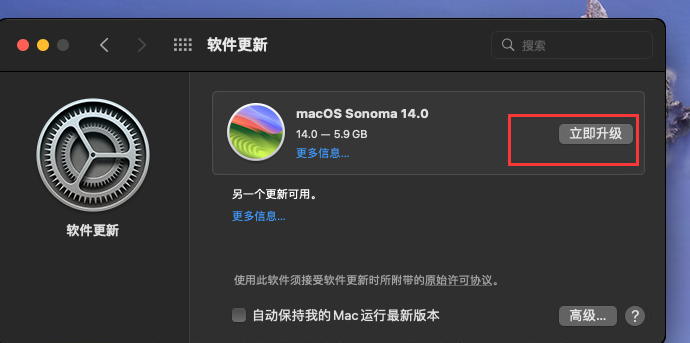
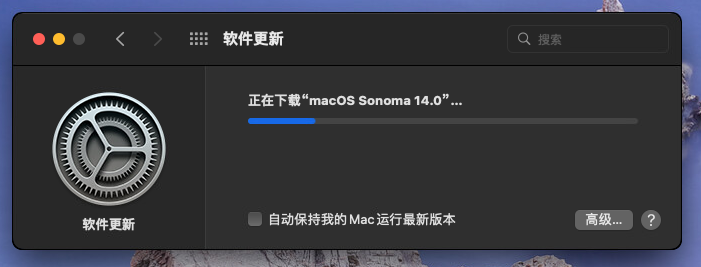
升级完成之后重启,所以千万不要手贱升级系统。

用快照恢复
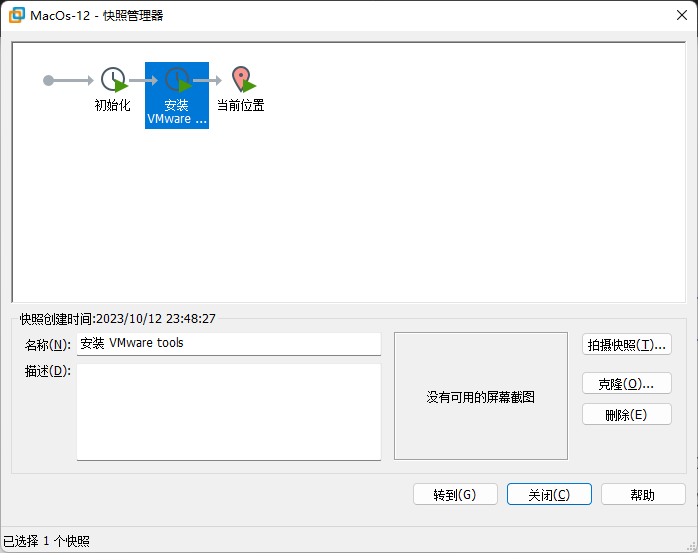
系统马上恢复!
