什么是成交型网站建设提高工作效率英语
书接上篇,我们了解了如何快速创建一个脚手架,现在我们来学习如何基于vite创建属于自己的脚手架。在创建一个新的组件时,要在新建文件夹中打开终端创建一个基本的脚手架,可在脚手架中原有的文件中修改或在相应路径重新创建!
详细创建过程可点击“如何创建一个脚手架”查看
一、单组件开发
1、介绍
单文件组件 (即 .vue 文件) 是一种特殊的文件格式,使我们能够将一个 Vue 组件的模板、逻辑与样式封装在单个文件中。比如:
<template><div class="header-comp"><h3>这是第一个组件程序</h3></div></template><script>export default {name: 'Header'}</script><style scoped>.header-comp{border: 3px solid red;}</style>(1)在Header.vue文件里(在components目录中创建vue文件名为Header.vue),<template>写HTML结构,像展示商品列表组件;
(2)<script>export default导出一个对象,这个对象代表了该组件的相关配置和属性;其中name: 'Header'给组件指定了一个名称为Header,这个名称在调试、递归组件等场景下可能会用到,方便在Vue应用中对组件进行识别和引用。
(3)<style>写样式,加scoped表示这个样式只会作用于当前组件内部的元素,避免全局样式污染,让代码模块化、可维护,团队协作分工明确。
这段代码定义了一个简单的Vue组件,包含了组件的结构、基本属性配置以及样式设定,可在Vue项目中作为一个独立的功能模块被使用并展示相应的内容和样式。
2、单文件如何运行
Vite会根据main.js文件中挂载的根组件(通常是App.vue)来渲染页面。如果要查看单组件,需要在App.vue中使用你开发的单组件。如:
<template><div><Header /></div>
</template><script>
import Header from './components/Header.vue';export default {name: 'App',components: {Header}
};
</script><style></style>(1)在<template>中,利用<div>包裹整个页面的主要内容,其中包含一个<Header/>组件标签,表明当前的App组件中使用了名为Header的组件(要引用那个.vue文件就写该文件名)。
(2)在<script>中
- 通过import语句从要引用的文件路径中引用组件(Header组件),使App组件可以使用Header组件。
- 再通过export default导出一个对象,这个对象代表了App组件的配置信息。
- name: 'App':给这个组件定义了一个名称为App,在调试工具或者进行组件递归引用等场景下,这个名称有助于识别组件。
- components: { Header }:这里定义了一个名为components的对象属性,将引入的Header组件添加到其中,使得在模板部分可以直接使用<Header />这种简短的标签形式来调用该组件,如果没有在这里注册,在模板中使用组件就会报错。
拓展
自闭合标签(<Header />):这种写法更加简洁,适用于组件没有内容插槽(即不需要在组件标签内部添加其他内容)的情况。
双标签(<Header></Header>):当组件定义了插槽,需要在使用组件的地方往组件内部添加内容时,双标签形式就很有用。
打开浏览器访问项目对应的网址则出现以下内容。
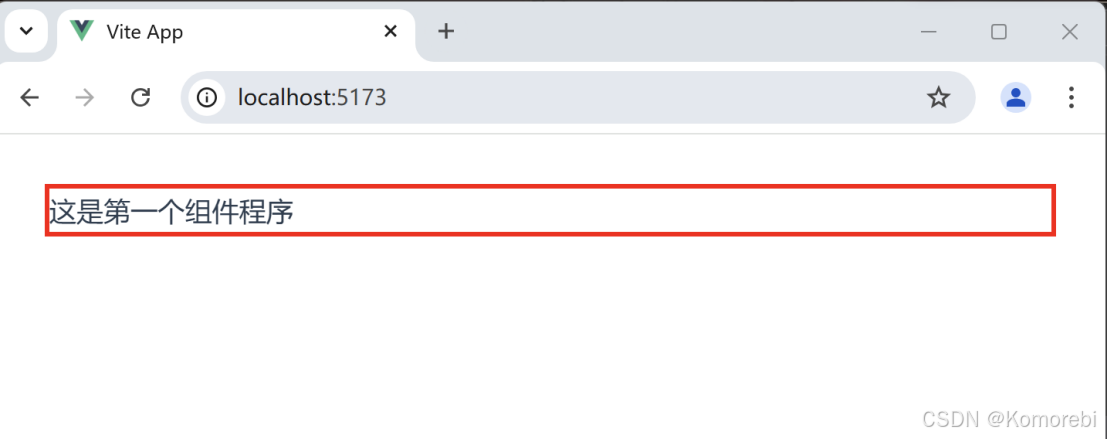
这段代码完整地构建了一个简单的Vue组件,涵盖了组件的视觉呈现(通过 <template>)、逻辑定义(通过 <script>)以及样式设置(通过 <style>)三个重要方面,可在Vue项目中作为一个基础的功能单元进行集成和使用。
3、弹窗提示
通过简单的单组件开发我们可以发现,里面的部分内容与我们之前所学的知识相似,或许我们也可以用该特性创建组件的其他功能,以弹窗提示为例,我们创建一个组件,当点击按钮时会出现弹窗提示我们。
(1)与前面一样先创建一个.vue文件,命名为Nav,大致内容与前面的Header.vue文件相似,不同的是,我们要在div内创建一个button按钮,并绑定一个事件,通过v-on:click="alert_msg"指令,将按钮的点击动作与名为alert_msg的函数进行关联,当按钮被点击时,会触发相应的函数执行。
(2)在<script setup>中,定义一个函数,用于当被调用时弹出一个警告框。
代码如下:
<template><div class="nav-comp"><h3>这是第二个组件程序</h3><button v-on:click="alert_msg">点击我</button></div>
</template><script setup>
const alert_msg = () => {alert('按钮被点击')
}
</script>
<style scoped>
.nav-comp {border: 3px solid red;
}
</style>App.vue的内容与调用Header文件一样,只需修改对应文件名和路径即可,注意路径不要写错,也可以直接添加Nav文件名,这样则会同时调用两个,这里我就只调用Nav文件
<template><div><Nav /></div>
</template>
<script>
import Nav from './components/Nav.vue'
export default {name: 'App',components: {Nav},
}
</script>
<style></style>打开浏览器访问项目对应的网址则出现以下内容:
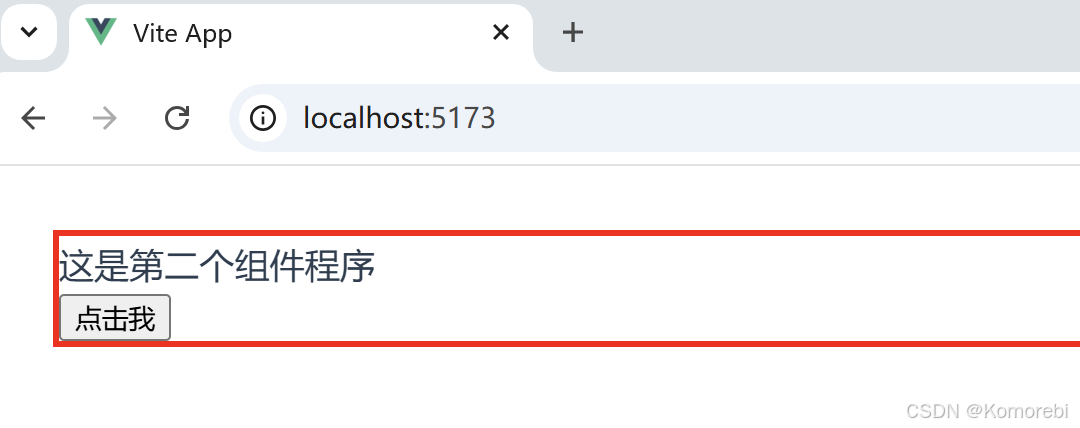
点击按钮后
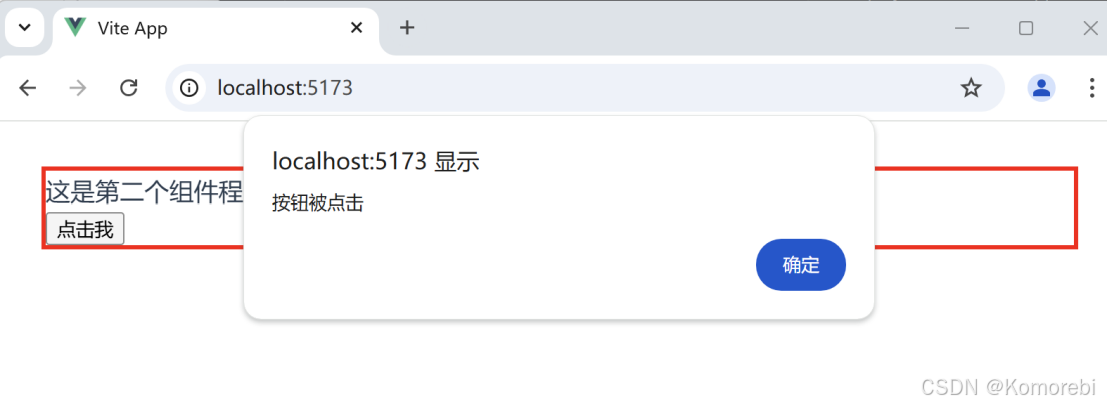
二、父组件向子组件传递数据
在Vue框架中,父组件向子组件传递数据通常是通过使用props属性来实现的。props是子组件用来接收来自父组件的数据的一个自定义属性。父组件通过在模板中绑定props到子组件标签上,将数据传递给子组件。子组件则在其props选项中声明接收的数据,并可以在其模板或计算属性中使用这些数据。
1、父组件的定义(App.vue)
(1)<template>
父组件需要在模板中使用子组件标签,这里使用了Header子组件,通过v-bind(简写:)将数据绑定到子组件的props属性上。如:将userName和userAge这两个数据分别绑定到子组件的propName和propAge属性上,实现了从父组件向子组件传递数据的操作。
<template><div><Header :propName="userName" :propAge="userAge" /></div>
</template>(2)<script>
通过import语句引入了Header.vue这个子组件,以便在父组件的模板中使用它。然后定义了两个常量userName和userAge,并分别赋予了具体的值。这里的userName和userAge就是要传递给子组件的数据。
<script setup>
import Header from './components/Header.vue';
const userName = '李四';
const userAge = 25;
</script>2、子组件(Header.vue)
(1)<template>
子组件的模板部分目前只是简单地展示了一个文本“我是页面头部(子组件)”,后续可以根据需求进一步扩展这里的展示内容,比如展示从父组件接收到的姓名和年龄等数据。
<template><div><h3>我是页面头部(子组件)</h3></div>
</template>(2)<script>
<script setup>const props = defineProps(["propName", "propAge"])console.log(props);
</script>- defineProps(["propName", "propAge"])是Vue 3中定义组件接收父组件传递属性的方式。它声明了这个子组件会接收来自父组件的propName和propAge两个属性。
- const props = defineProps(["propName", "propAge"]);将接收到的属性赋值给props常量,方便后续在组件内使用这些属性。
- console.log(props);这行代码会在浏览器控制台打印出接收到的属性对象,这样可以直观地看到父组件传递过来的数据内容,格式类似于{ "propName": "李四", "propAge": 25 },具体的值取决于父组件传递的数据。
(3)<style>与前面内容一样
-
<style scoped>div {width:25%;background-color: rgb(238, 156, 156);color: blanchedalmond;} </style>打开浏览器访问项目对应的网址则出现以下内容:
数据传递的注意事项
props传递的数据是单向下行的,即父组件的数据更新会流向子组件,但子组件不应直接修改props数据。
如果需要在子组件中转换或使用props数据,可以使用计算属性或定义本地data属性。
对于对象或数组类型的props,由于它们是通过引用传递的,子组件中对这些props的修改会影响父组件的状态。
通过这种方式,Vue实现了组件间的数据流动和通信,使得父子组件之间的数据关系清晰且易于管理。
三 、子组件向父组件传递事件
通过父组件向子组件传递数据的学习,我们已经知道了 Vue 是单向下行数据流, 子组件更改 props 中的数据不会触发父组件数据的改变, 但是由于响应式原理,父组件数据的改变会导致子组件 props 中值的改变。
那么我们怎么才能在子组件中改变父组件中的数据呢?
1、子组件(Header.vue)
(1)<template>
子组件通过emit触发自定义事件。 每个按钮都绑定了一个点击事件,分别是sendGetPersonData和sendAddPersonData,点击这些按钮将会触发相应的方法来执行特定操作,即向父组件发送数据。
<template><div><button @click="sendGetPersonData">发送getPerson数据</button><button @click="sendAddPersonData">发送addPerson数据</button></div>
</template>扩展
在Vue.js里,$emit是Vue实例的一个方法。它的作用是在子组件中触发一个自定义事件,并且可以携带数据传递给父组件。就像是子组件在特定场景下(比如按钮点击、数据变化等)发出一个信号,父组件如果监听了这个信号,就能收到并做出相应的反应。
(2)<script>
通过定义了两个可以向父组件发射的自定义事件,分别是getPerson和addPerson。当点击按钮时,会通过emit对象发送一个事件并同时传递一个数据对象给父组件
<script setup>const emits=defineEmits(["getPerson","addPerson"]);const sendGetPersonData=()=>{emits("getPerson",{name:"李雷",age:20});};const sendAddPersonData=()=>{emits("getPerson",{name:"韩梅梅",age:18}); }
</script>(3)<style scoped>
与前面一样
<style scoped>div{width: 50%;background-color: antiquewhite;}
</style>2、父组件(App.vue)
(1)<template>
在App.vue的模板中,引入了Header.vue组件,并通过@符号监听Header组件发射的getPerson和addPerson自定义事件。
<template>
<div><Header @getPerson="handleGetPerson" @addPerson="handleAddPerson"/></div>
</template>(2)<script setup>
通过import语句引入了Header.vue组件,以便在App.vue中使用。通过箭头函数,当接收到该事件时会在控制台打印出接收到的事件以及相关的数据内容。
<script setup>import Header from './components/Header.vue';const handleGetPerson=(data)=>{console.log("接收到getPerson事件,数据为,",data);};const handleAddPerson=(data)=>{console.log("接收到addPerson事件,数据为,",data);}
</script>
<style></style>主要目的是实现子组件Header.vue向父组件App.vue发送自定义事件及相关数据,父组件通过监听这些事件来处理接收到的数据。
打开浏览器访问项目对应的网址则出现以下内容:
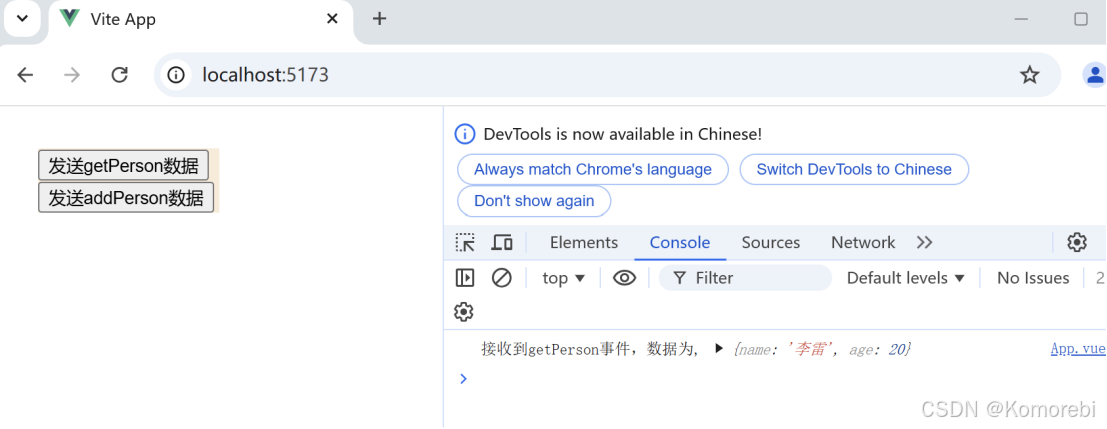
点击第一个按钮时
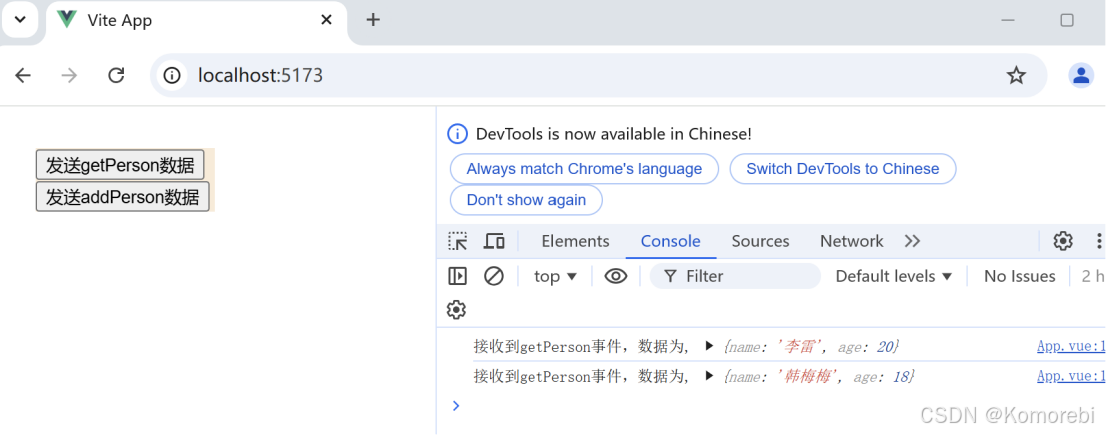
点击第二个按钮时
四、跨组件通信
跨组件通信是指在一个应用中,不同组件之间进行数据传递或事件通知的过程。如:通过Vue的自定义事件机制,实现了下级组件向上级组件发送数据的跨组件通信功能。当点击下级组件中的按钮时,会将指定的数据发送给shang,App.vue接收到数据后会在控制台打印相关信息,并在页面上展示接收到的数据内容。
1、下级组件(Header.vue)
(1)<template>
设置一个按钮绑定了sendDataToParent,点击按钮将触发数据发送操作,目的是把数据发送给上级组件(App.vue)
<template><div><button @click="sendDataToParent">发送数据给上级组件</button></div></template>(2)<script setup>
通过import { defineEmits } from 'vue'引入了Vue中用于定义可发射自定义事件的函数。再定义一个自定义事件,用于向父组件发送数据。通过emits对象发射事件,并同时传递一个数据对象给父组件。这样就完成了从下级组件(Header.vue)向上级组件(App.vue)发送数据的准备工作。
<script setup>import { defineEmits } from 'vue';const emits = defineEmits(['getData']);const sendDataToParent = () => {emits('getData', { name: '张三', age: 25 });};</script>2、上级组件(App.vue)
(1)<template>
首先引入Header.vue组件,通过@监听Header组件发射的自定义事件。通过v-if指令判断是否有值。如果有值(即接收到了来自子组件的数据),则展示接收到的数据内容
template><div><Header @getData="handleDataReceived" /><div v-if="receivedData">接收到的数据:姓名 - {{ receivedData.name }}, 年龄 - {{ receivedData.age }}</div></div>
</template>(2)<script setup>
首先通过import语句引入了Header.vue组件,以便在App.vue中使用。通过ref创建一个响应式数据,用于存储从子组件接收到的数据。再使用箭头函数设置当接收到该事件时,会在控制台打印出接收到的事件以及相关的数据内容,然后将接收到的数据赋值给receivedData.value,以便在模板部分能够正确展示出来。
<script setup>
import Header from './components/Header.vue';
import { ref } from 'vue';// 用于存储接收到的数据
const receivedData = ref(null);
// 处理从子组件接收到的数据
const handleDataReceived = (data) => {console.log('接收到来自子组件的数据:', data);receivedData.value = data;
};
</script>打开浏览器访问项目对应的网址则出现以下内容:
点击按钮后