o2o网站建设新闻seo优化内容
iMazing 3中文版免费下载是一款兼容Win和Mac的iOS设备管理软件。iMazing 3能够将音乐、文件、消息和应用等数据从任何 iPhone、iPad 或 iPod 传输到 Mac 或 PC 上。
使用iMazing 3独特的 iOS 备份功能保证数据安全:设定自动无线备份时间并支持快照;将备份保存到外接驱动器和网络附属储存,等等。 了解详情 计划备份 自动归档 自动清理将任意内容传输至 iPhone 和 itunes.
iMazing Win-安装包: https://souurl.cn/cnEXJ7
iMazing Mac-安装包: https://souurl.cn/tf6ZeP
管理您的 iMazing 许可证
激活 iMazing
管理您的设备许可证
将设备链接到您的许可证
查看许可设备
扩展您的许可证
从 iMazing 中删除您的许可证
从许可证中删除设备
升级到无限设备计划
管理基于计算机的许可证
从 iMazing 中删除您的许可证
查看、延长或取消您的 iMazing 计划
检索您的许可证代码
1. iMazing 无需注册即可免费下载和安装
iMazing 无需注册即可免费下载和安装。许多功能无需许可证即可使用,其他功能(称为高级功能)需要许可证。

2. 激活 iMazing
激活是指在 iMazing 中输入有效许可证代码的过程。验证许可证后,iMazing 将激活,并根据您的许可证类型解锁功能。
如何激活 iMazing:https://souurl.cn/UppPXw
在上方工具栏中,点按“iMazing 许可证”
将显示欢迎窗口。单击输入许可证代码
复制并粘贴或键入您的许可证代码,然后单击提交
iMazing 现在应该在该计算机上激活,并且 iMazing 许可证按钮将消失。从那时起,许可证管理将在“许可证”菜单中进行。
⚡ 无法激活?请参阅此激活故障排除文章。
3. 管理您的设备许可证
设备许可授予在特定 Apple 移动设备上无限制地使用 iMazing 的高级功能。您可以在任何 Mac 或 PC 上使用相同的设备许可证激活 iMazing。
💡 如果您的许可证代码以 id 开头,或者您拥有 iMazing Unlimited 设备 / 商业 / 配置器订阅,您可以直接跳转到管理基于计算机的许可证。
将设备链接到您的许可证
每当您在尚未链接到许可证的设备上使用高级功能时,iMazing 都会提供链接。在下面的屏幕截图中,我们正在从Amy的iPhone导出照片,该设备尚未链接到许可证:
从这里,您可以:
点按“稍后”按钮,继续在 Amy 的 iPhone 上使用 iMazing 的免费功能。
单击“链接并继续”以将 Amy 的 iPhone 永久关联到您的 iMazing 许可证,并解锁该设备无限制地使用所有高级功能。
查看许可设备
“许可证”菜单的“查看许可证”选项将打开“许可设备”窗口:
从这里,您可以查看哪些设备已链接到您的许可证。此处列出的设备标识符是唯一标识符,如果需要,您可以将其传达给我们的支持团队。
扩展您的许可证
您的 iMazing 裝置授權支援有限數量的 Apple 移動裝置。如果您的许可证已完全使用,则使用新设备访问高级 iMazing 功能将显示以下屏幕:
单击扩展许可证按钮以打开许可证存储并扩展许可证,以便它可以支持更多设备。
从 iMazing 中删除您的许可证
您可以使用“许可证”菜单的“删除许可证”选项从 iMazing 中删除许可证:
删除许可证后,iMazing 将返回试用模式。请注意,在另一台计算机上激活 iMazing 之前,您无需从一台计算机上删除设备许可证 - 设备许可证仅绑定到您获得许可的移动设备,并且可以在任意数量的 macOS 或 Windows 计算机上使用。
从许可证中删除设备
将特定的 iPhone、iPad 或 iPod 设备链接到您的许可证是永久性的,无法撤消。许可设备可在任何 Mac 或 PC 电脑上的整个生命周期内与所有 iMazing 更新(包括主要版本)一起使用。
💡 您是否错误地将设备链接到许可证,或者 iMazing 无法对特定设备执行预期任务?请立即与我们联系并提供详细信息。我们信任我们的用户,并将快速处理合法请求。
升级到无限设备计划
如果您每年将 iMazing 的高级功能用于 4 台以上的新设备,则无限设备计划可能更有利。请联系我们的支持团队了解升级条件。
4. 管理基于计算机的许可证
基于计算机的许可证允许在有限数量的 Mac 或 PC 计算机上激活 iMazing。使用 iMazing 管理的 Apple 移动设备数量不受限制。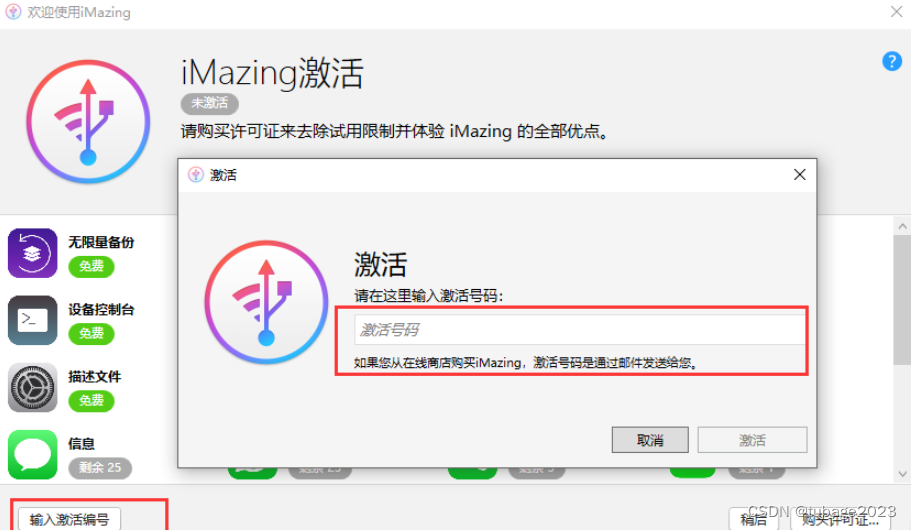
该类型的许可证包括:
iMazing 无限设备许可证
爱玛辛营业执照
iMazing 配置器
iMazing 2 旧版许可证(许可证代码格式)id*****
从 iMazing 中删除您的许可证
您可以使用“许可证”菜单的“删除许可证”选项从 iMazing 中删除许可证。这将释放一个席位,以便您可以在另一台 macOS 或 Windows 电脑上使用相同的许可证代码激活 iMazing。
⚡ 如果您忘记从无法再访问的计算机中删除许可证,请联系我们的支持团队并提供您的许可证代码。
查看、更新或取消您的 iMazing 计划
如果您选择了订阅计划,则可以在“许可证”菜单的“计划”子菜单中轻松管理它:
从这里,您可以轻松查看和管理您的计划。
查看计划
单击“查看计划”选项以查看计划的类型、席位数和帐单信息:
管理计划
单击“管理计划”选项,iMazing 将向您发送一封电子邮件,其中包含用于更新付款方式、向许可证添加更多席位或取消订阅的链接。以下是电子邮件的外观:
通过此电子邮件,您可以:
以按比例定价向现有计划添加更多席位,在单个订阅下保持计费干净。
更新您的付款方式,以防结算失败。
取消订阅。您的许可证将保持完全有效,直到订阅期结束。
