网站建设竞争对数分析重庆电子商务seo
gulimall项目笔记:P54三级分类拖拽功能实现
技术方案
采用ElementUI的Tree树形控件实现分类拖拽功能
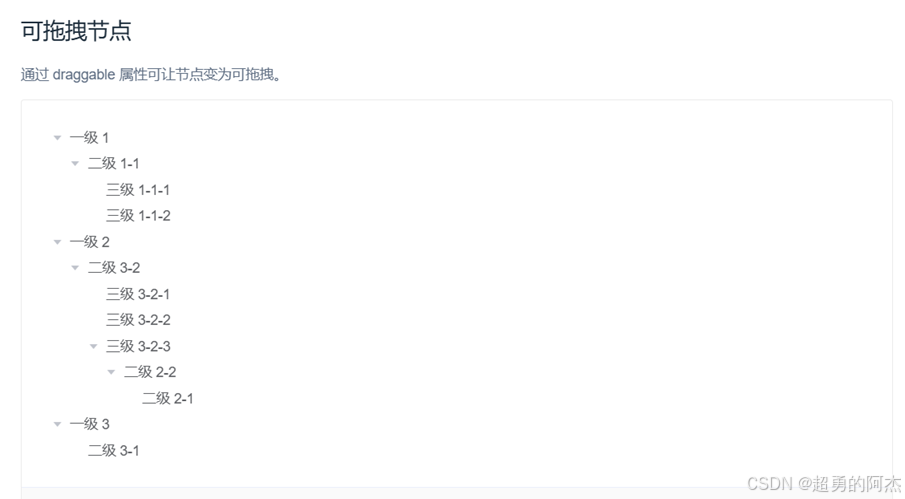
功能规则
- 层级限制:分类结构最多支持3级
- 拖拽验证:通过ElementUI的
allow-drop事件实现
核心参数
allow-drop事件包含三个关键参数:
draggingNode- 拖拽中的节点dropNode- 目标放置节点type- 拖拽类型(‘prev’、‘inner’、‘next’)

参数draggingNode和dropNode包含两个重要属性:
childNodes- 子节点集合level- 节点层级
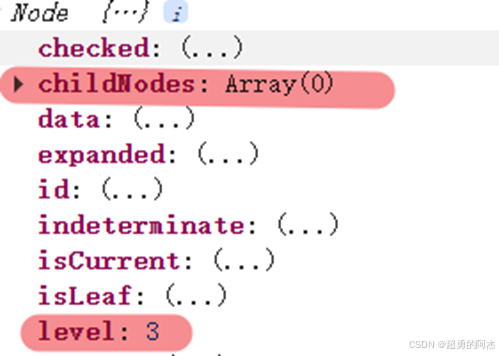
实现逻辑
1.计算子树深度(countNodeLevel方法)
首先通过计算当前拖拽节点draggingNode的最大子树的level。
countNodeLevel(node) {if(node.childNodes != null && node.childNodes.length > 0){for(let i = 0; i< node.childNodes.length; i ++){if(node.childNodes[i].level > this.maxLevel){this.maxLevel = node.childNodes[i].level;}this.countNodeLevel(node.childNodes[i]);} }
}
然后在计算出draggingNode的最大深度deep。
deep = this.maxLevel – draggingNode.level + 1
基于这些参数,三级目录结构可归纳为三种情况:
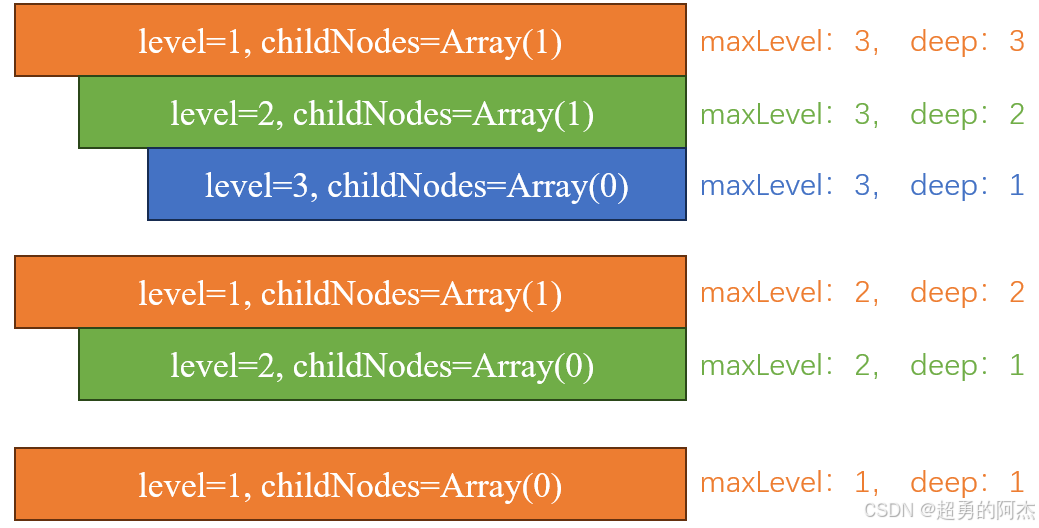
2.允许拖拽判断(allowDrop方法):
然后根据拖拽放置类型type(inner表示插入目标节点内,prev或next表示放置在目标节点前后)来判断是否允许拖拽。如果是inner类型,判断deep + dropNode.level <= 3;如果是before或after类型,判断deep + dropNode.parent.level <= 3。
if (type == ‘inner’) {return deep + dropNode.level <= 3;
}else{return deep + dropNode.parent.level <= 3;
}
扩展
如果层级限制的分类结构最多支持n级,我们只需要把<= 3改成<= n即可。
