南昌哪里学做网站百度公司官网入口
“从BNB Beacon Chain,到BNB Chain,再到BNB Greenfield ,三位一体的 BNB 生态格局正式形成。 ”
在今年的2月1日,币安发布了分布式存储链BNB Greenfield,根据白皮书信息,它的特别之处在于其不仅具备基于SP(分布式存储商,可以理解为存储节点)获得的分布式存储的能力,它还具备可编程可计算的能力,兼容EVM。该链是币安生态继发布了BNB Beacon Chain、BNB Chain后,又将发布的第三条生态链, 该链将以侧链的形式更好的“辅助”BNB Chain生态的运行。
而从DSN(Decentralized Storage Network)赛道的角度看,目前以Filecoin(IPFS)、Arweave、Sia、Storj等为代表的主要生态,与智能合约的可互操作性较差,虽然Filecoin意在第三阶段上线FVM(虚拟机),但这似乎仍旧较为遥远,所以具备计算+存储特性的BNB Greenfield,与上述几个存储生态还是存在本质上的差别的。此外,BNB Greenfield的推出,对于BNB Chain生态的发展将有着十分重要的推动作用,并成为其Web3生态发展的一大重要优势。
01
以 Amazon、Azure、谷歌等为代表传统云服务商,在云计算、API和其他SaaS产品上能够提供更为出色的服务,但事实上用户缺乏数据所有权、数据泄露和中断、高度审查机制以及应用的高成本等缺陷的日益突出,也进一步成为了DSN赛道发展的理由,并涌现出了以Filecoin(IPFS)、Arweave、Sia、Storj等为主要代表的DSN生态(他们占据了主要的DSN存储份额),而该赛道也是Web3领域发展的一个重要叙事方向之一。
分布式存储的基本思路在于,将内容/文件以分散且加密的形式,存储在不同的节点中,而不是集中存储在单一的存储容器内,以达到防止数据泄露中断、抗审查、降低成本以及重新掌握数据所有权的目的,但不同的DSN系统实现的技术手段与机制不同。
根据高盛分析师Hunter Lampson所统计(去年8月)的DSN领域存储数据显示,以内容寻址为特点的Filecoin(IPFS)在四个主要DSN系统中存储数据所占据的比例最高,达到了90%以上,而根据Filecoin基金会发布的2022年度报告,Filecoin总存储容量接近19 EiB,占全球总存储容量的1%,这意味着Filecoin目前的占比将有所上升,并且仍旧具备可观的市场潜力。
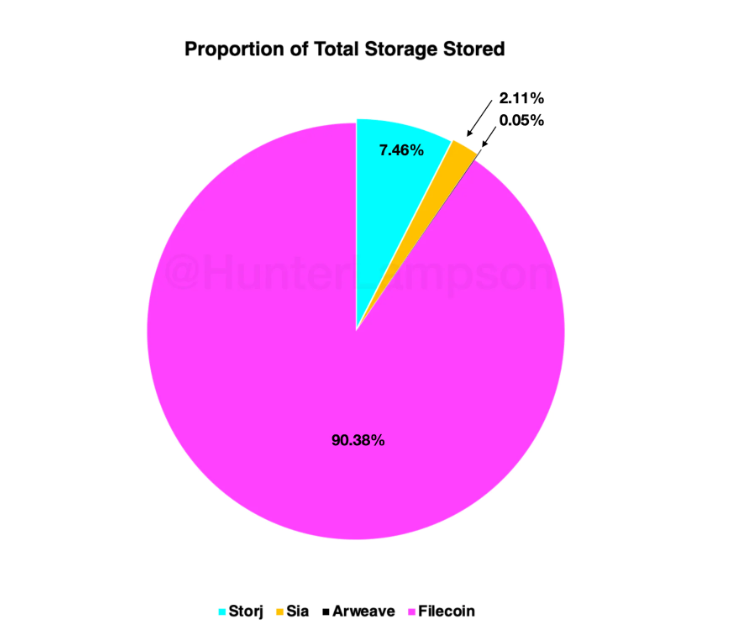
在Filecoin后则是以赖擦除编码和卫星节点来存储数据为特点的Storj,其的数据存储量占比约为7.5%,其次是基于POW作为共识的老牌存储系统Sia占比约2.11%(它并不被看好),Arweave仅占0.05%(以永久存储为特点,很多NFT项目以及内容平台,宣传上更喜欢使用AR作为存储手段,潜力不错)。
DSN赛道是一个潜力赛道,一方面其体量距离Web2云服务商仍旧很远,同时越来越多的Web2、Web3应用对其展现出兴趣,但我们看到现有的DSN系统所能为需求方提供的服务仍旧有限。
虽然Filecoin(IPFS)、Arweave、Sia、Storj等在存储模型上都能够实现相对可靠的分布式存储,但其对不同类型数据的支持上,仍然难以覆盖,并主要能够处理无需频繁访问的冷数据,比如用在NFT所对应的数据内容、区块链系统的数据同步等。而目前没有能够为这些DSN系统服务的内容交付网络(CDN),并且这些系统在检索速度(当然也包括写入)与成本上都存在一定的问题,所以它们在存储和处理访问频繁的热数据方的能力相当弱,这意味着它们并不能对一些访问频繁的内容流比如视频流、音乐流动进行支持。
从Web2云服务商看,它们不仅能够提供存储,也能够提供计算,比如我们可以将网站直接部署在Web2云上,并在其提供的云生态中享受所有的配套服务,多数时候它能够保证应用的运行(当然审查同样可怕)。所以我们看到,一些DeFi协议、NFT项目等更喜欢以DSN作为存储手段,但他们的前端仍旧是部署中心化的云上,比如Uniswap、AAVE等。所以对于一众Web3应用,是难以抵御云服务商的单点故障以及审查的,这也就是为什么那个基于Nostr 底层 开发的 Damus,尽管极其难用(使用去中心化的中继器来分发消息,抗审查),但仍旧备受关注的原因。
当然,DSN系统作为分布式的数据体系,本身有望通过更多的场景为数据释放数据原生价值,但非可编程以及不具备计算能力,这使得这些数据除了被冷存储、被外界低频索引调用外,没有任何新的价值。虽然 Protocol Labs 表示第三阶段 Filecoin 将上线 FVM虚拟机以增加计算能力,但从过往 Protocol Labs 的“守约”能力,FVM的开发周期以及上线进度是不敢恭维的。
所以在目前DSN赛道整体的发展先转看,具备计算+分布式存储能力的BNB Greenfield 是具备一定前瞻性的。
02
BNB Greenfield链本身是以存储链为定位,并且它的分布式存储技术在逻辑上并不复杂。BNB Greenfield上主要包含了SPN(存储提供商网络)与 Greenfield 区块链网络,其中SPN由SP(存储供应商)构成,即作为具备专业存储能力或者闲置存储资源的用户在网络中注册后,可以通过质押BNB的方式成为供应商,并通过相应的共识机制来分配存储任务以获得奖励。而在 Greenfield 区块链网络中,还存在验证者,以对SP数据可用性进行检验。
而检验过程类似于Optimism的挑战机制,即Greenfield也会由验证者以随机的方式,对SP发起挑战事件,来对SP的数据可用性进行挑战并设定罚没机制。挑战成功则发起者获得奖励,节点受到惩罚,挑战失败的话则该数据会有一个冷冻期不会再被发起挑战,从而避免资源浪费。
而在BNB Greenfield启动初期,创世之初的初始验证人集合,会先锁定一定数量的BNB到BSC上的“Greenfield Token Hub”合约中,并且该合约也将用作BNB创世后转账的原生桥的一部分。这些初始锁定的BNB将用作验证者的抵押和早期燃料费,以作为早期的启动机制。
所以,我们看到BNB Greenfield并没有发行通证,而是直接将BNB通过跨链桥“牵引”到BNB Greenfield上(当然这个桥也用来传输数据与信息),这十分有利于BNB Greenfield的早期启动。从其他的分布式存储生态看,代币价值体系与系统的可持续性是直接挂钩的(单一锚定性),比如Filecoin在放弃补贴存储成本后,存储成本的升高导致存储需求的下降,或许对FIL的价值产生严重的影响,而反过来在币本位的存储成本增加,或者FIL本身价值基本盘薄弱而对Filecoin产生消极影响等,甚至会陷入一些死亡螺旋。

BNB Greenfield目前没有公布经济模型, 但我们看到,BNB是本身一个受多个复杂因素影响的多职能通证,它的赋值可能包括币安CEX、BNB Chain、BNB Beacon Chain、Biancen NFT平台甚至是BNB Greenfield等,BNB的价值并非单一由BNB Greenfield决定,所以BNB Greenfield相对于其他存储生态,在价值的调控、存储成本的定价(即便是机制是不合理的),可能会更加稳定。此外,这也为BNB向存储方向赋能,并且质押的开启同样有利于BNB价值的攀升。
当然,计算是BNB Greenfield的一个十分重要的亮点,因为它是一个支持EVM的可编程存储系统。从现有的区块链系统看,存储与计算通常是割裂的,比如具备良好计算能力的Layer1、Layer2通常需要链下存储或者使用外部的DSN系统存储数据。所以这对于开发者来说,在获得良好计算能力的同时,不得不额外的获得存储资源,比如一个NFT协议布置在链上,存储的数据可能存储在Filecoin上,但前端又依赖于AWS,外接系统数量的增加正在增加“犯错”的概率。此外,缺乏可编程性与计算能力,也正在让现有的一些DSN系统在应用场景上的支持上有限。
所以BNB Greenfield本身兼具存储与计算,这意味着开发者可以直接在BNB Greenfield上存储数据,并获得计算资源比如直接基于BNB Greenfield部署网站与应用,而不再对AWS等产生依赖,为用户数据所有权以及抗审查等打下基础,其能够提供的工具包括数据端点、交易接口、P2P 网络和相应的SDK等
从现有的DSN系统看,存储的直接用户通常是TO B(或者开发者),而不是直接面向用户,我们看到Filecoin、Arweave等的个人用户并不多,所以BNB Greenfield也有望基于用户同步工具来享受个人存储业务,即为每一个用户都“配置”一个去中心化的数据保险箱,而使用过程或许将类似于Apple Cloud这类面向个人的云储产品。基于此,用户有望可以直接读取、共享甚至基于智能合约执行数据,用并进一步将其赋值成资产,以获得财务价值、金融化场景,并进一步演化成新形态的创作者经济生态、社交生态等。
此外,寄托于具备存储与计算功能的BNB Greenfield,或许有望会出现新形态的 Web3 CDN(内容交付网络)二级基建,以在存储和处理热数据上获得新能力的提升,来进一步提供稳定、即时的数据传输能力,来为此类平台提供的低延迟流媒体服务,并对视频流或其他类型内容的实时交付。
03
BNB Greenfield虽然是一条新的存储链,但它更多的也被定义为BNB Chain的一条侧链,能够通过跨链桥来与BNB Chain实现信息、资产的交互,所以通过原生的“桥”的互操作它能够实现BNB Chain上应用数据的分布式存储与互通,并形成双方数据的相互读取。BNB Chain承担了dapp部署、数据资源镜像、跨链和共识 Greenfield则承担支付、数据资源、跨链和共识.
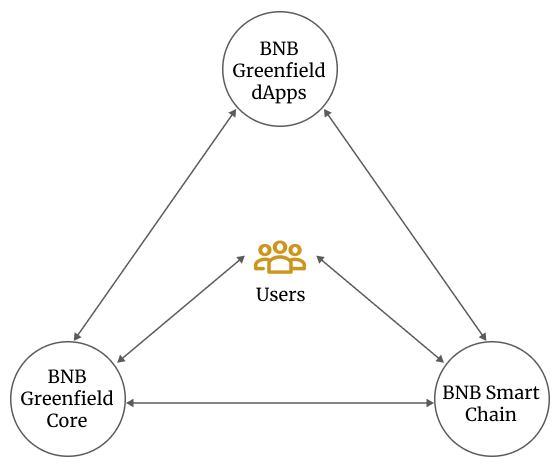
BNB Chain 作为以太坊的同构链,不仅支持 EVM (以太坊虚拟机),现有的 DeFi 或以太坊的其他 DApp 、工具都可以无缝迁移到BNB Chain上,这意味着 BNB Greenfield 同样具备该特性,BNB Chain现有的一些配套设施比如钱包、NFT平台以及浏览器等,都能够相集成且形成无障碍链接。而作为EVM系的链,虽然其没有像Solana、Atpos等形成自己的独特开发者群体,但低门槛、通用性同样有望吸引大量的开发者。
此外,BNB Greenfield是基于Layer0 Cosmos构建,它也有望进一步通过IBC系统来与现有的Cosmos链形成互操作, 并为除BNB Chain以外其他Cosmos系生态,原生基于互操作性提供存储+计算服务,以进一步扩大生态用户与内容丰富度。
目前,无论在生态的厚度、资金体量还是协议数上(540个),并且涵盖了行业内所设计到的几乎所有赛道,BNB Chain 的表现仅次于以太坊生态,而BNB Chain 的现有存量DAPP有望能够帮助BNB Greenfield撑起早期的启动,并吸引更多的增量开发者。
很直观的,BNB Greenfield的出现再一次为BNB赋能了新的场景,并通过借贷、质押、Gas消耗以及存储空间的定价促进了通缩,对于BNB价值基础护城河的提升绝对是有利的。
其实在此前很多人认为,未来公链的格局,将会是以太坊作为结算层(绝对Layer1),Layer2以及其他Layer1将通过桥来实现与以太坊的交互,并获得来自于以太坊所提供的安全。但币安的 Web3 体系正在进一步拓展、升级为BNB Beacon Chain(安全)、BNB Chain(应用)、BNB Greenfield(存储)三位一体的全新生态,以以太坊为“绝对”核心的格局,或许正在被撼动。
