青岛专业网站建设价格一键优化表格
一、iftop是什么
iftop是类似于top的实时流量监控工具。
作用:监控网卡的实时流量(可以指定网段)、反向解析IP、显示端口信息等
官网:http://www.ex-parrot.com/~pdw/iftop/
二、界面说明
=>代表发送数据,<= 代表接收数据
TX:发送流量
RX:接收流量
TOTAL:总流量
Cumm:运行iftop到目前时间的总流量
peak:流量峰值
rates:分别表示过去 2s 10s 40s 的平均流量三、常用参数
-i 指定需要检测的网卡, 如果有多个网络接口,则需要注意网络接口的选择,如:# iftop -i eth1-B 将输出以byte为单位显示网卡流量,默认是bit-n 将输出的主机信息都通过IP显示,不进行DNS解析 -N 只显示连接端口号,不显示端口对应的服务名称-F 显示特定网段的网卡进出流量 如iftop -F 192.168.85.0/24-h 帮助,显示参数信息-p 以混杂模式运行iftop,此时iftop可以用作网络嗅探器 ;-P 显示主机以及端口信息-m 设置输出界面中最上面的流量刻度最大值,流量刻度分5个大段显示 如:# iftop -m 100M-f 使用筛选码选择数据包来计数 如iftop -f filter code-b 不显示流量图形条-c 指定可选的配置文件 如iftop -c config file-t 使用不带ncurses的文本界面,以下两个是只和-t一起用的:-s num num秒后打印一次文本输出然后退出,-t -s 60组合使用,表示取60秒网络流量输出到终端-L num 打印的行数
-f 参数支持tcpdump的语法,可以使用各种过滤条件。四、进入界面后的操作
一般参数
P 切换暂停/继续显示
h 在交互界面/状态输出界面之间切换
b 切换是否显示平均流量图形条
B 切换显示2s10s和40s内的平均流量
T 切换是否显示每个连接的总流量
j/k 向上或向下滚动屏幕显示当前的连接信息
f 编辑筛选码
l 打开iftop输出过滤功能 ,如输入要显示的IP按回车键后屏幕就只显示与这个IP相关的流量信息
L 切换显示流量刻度范围,刻度不同,流量图形条也会不同
q 退出iftop主机参数
n 使iftop输出结果以IP或主机名的方式显示
s 切换是否显示源主机信息
d 切换是否显示远端目标主机信息
t 切换输出模式,一行或多行端口显示参数
N 切换显示端口号/端口号对应服务名称
S 切换是否显示本地源主机的端口信息
D 切换是否显示远端目标主机的端口信息
p 切换是否显示端口信息输出排序参数
1/2/3 通过第一列/第二列/第三列排序
< 根据左边的本地主机名或IP地址进行排序
> 根据远端目标主机的主机名或IP地址进行排序
o 切换是否固定显示当前的连接五、使用示例
1.显示网卡eth0的信息,主机通过ip显示
iftop -i eth0 -n2.显示端口号(添加-P参数,进入界面可通过p参数关闭)
iftop -i eth0 -n -P3.显示将输出以byte为单位显示网卡流量,默认是bit
iftop -i eth0 -n -B4.显示流量进度条
iftop -i eth0 -n(进入界面后按下L)5.显示每个连接的总流量
iftop -i eth0 -n(进入界面后按下T)6.显示指定ip 172.17.1.158的流量
iftop -i eth0 -n(进入界面后按下l,输入172.17.1.158回车)六、实战-找出最费流量的ip和端口号
网上找了一圈,全是粘贴复制的iftop命令使用,没说到点上
接下,请欣赏真正的表演
1.进入界面
iftop -i eth0 -nNB -m 10M-i 指定网卡,
-n 代表主机通过ip显示不走DNS
-N 只显示连接端口号,不显示端口对应的服务名称(不加会显示如ssh这样的服务名称,不便于排查)
-B 指定显示单位为Kb,默认是bit,太小!
-m 设置输出界面中最上面的流量刻度最大值,流量刻度分5个大段显示
进入后界面如下
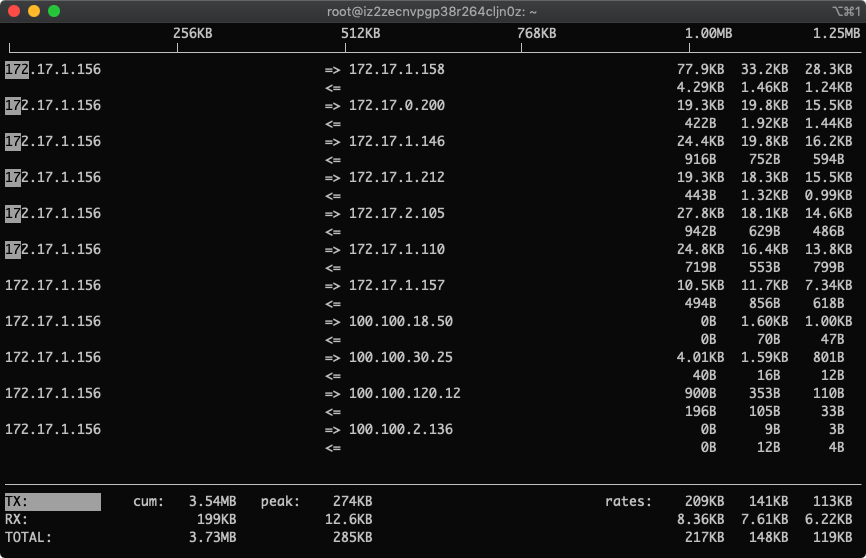
2.按下L显示流量刻度
L参数直接显示进度条,方便人类阅读,别说你能直接通过数字感知,小心被砍死
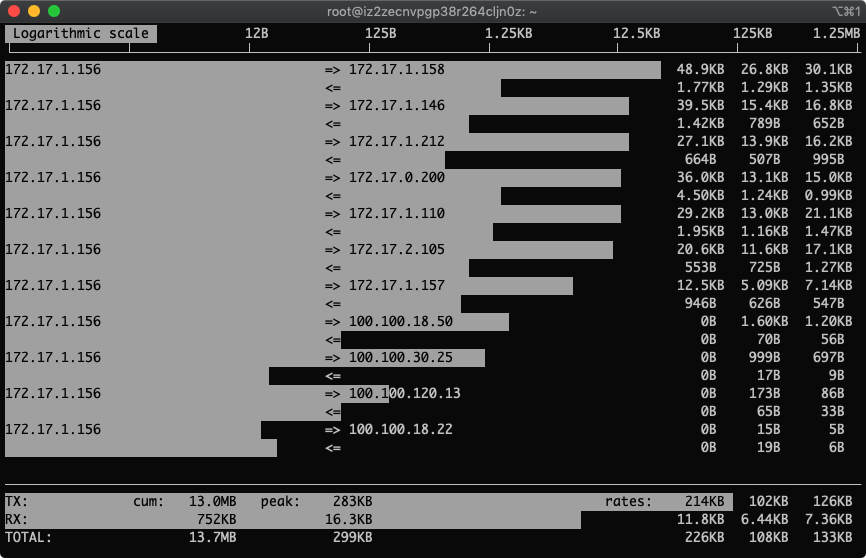
3.按下T显示总量
总得有个总数统计,看着方便!
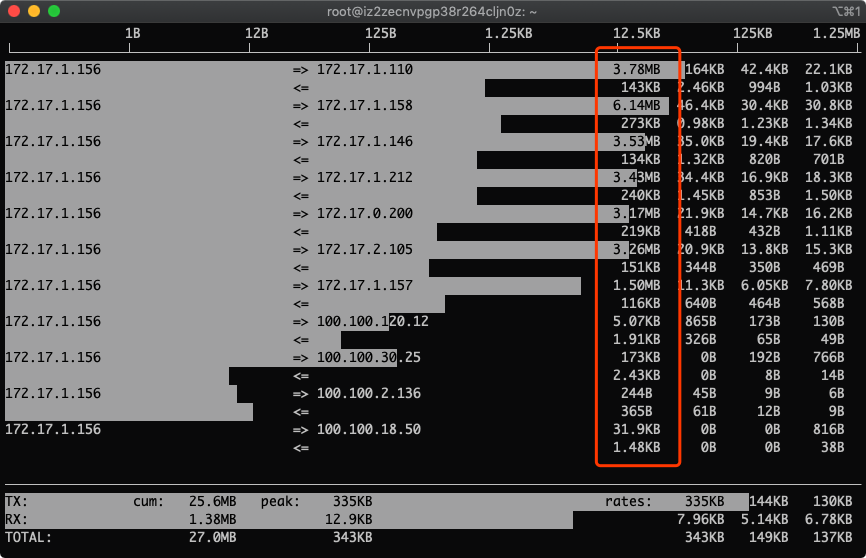
4.按下3,根据最近40s统计排序
用平均值来统计最权威点
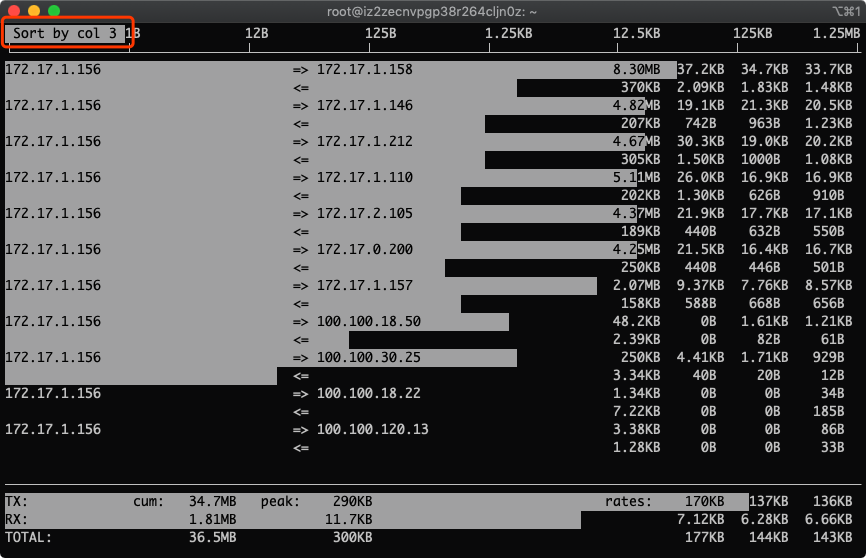
5.按下t,发送和接受合成一行
显示两行没什么意思,一行就够了!
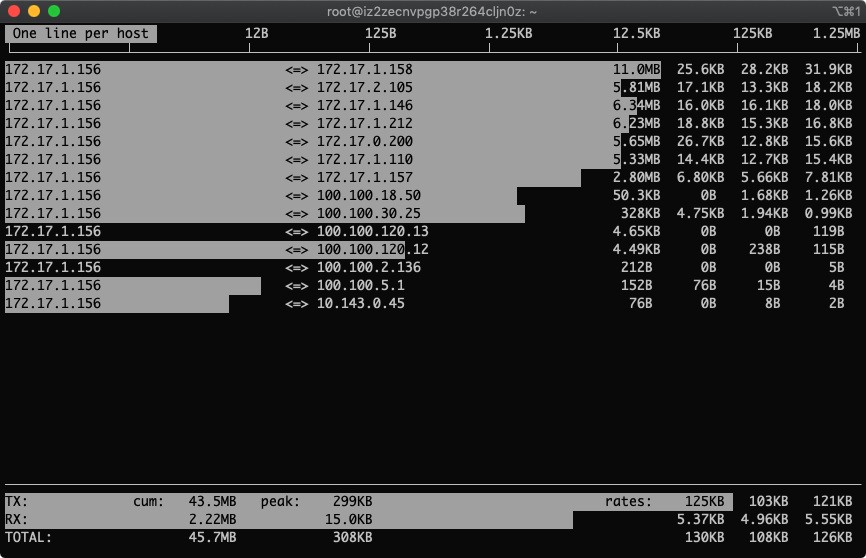
6.多按几次B,查看最近2s、10s、40s的统计
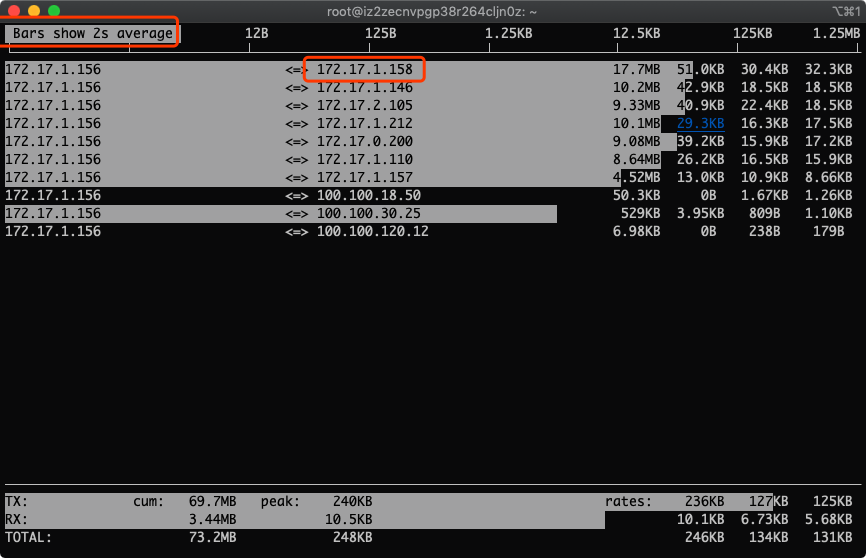
没错,图中的172.17.1.158就是我们找到的流量用得最多的IP
7.筛选指定IP 172.17.1.158
按下l, 输入172.17.1.158,出现如下
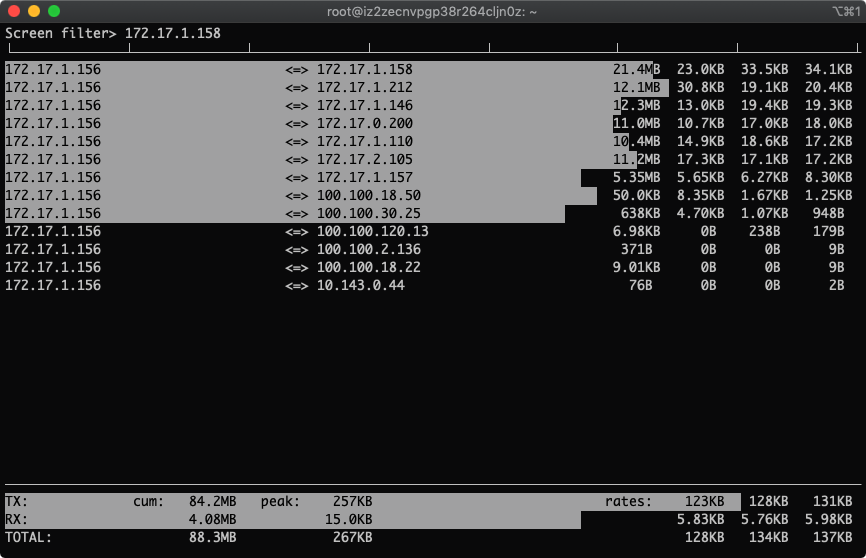
回车,生效
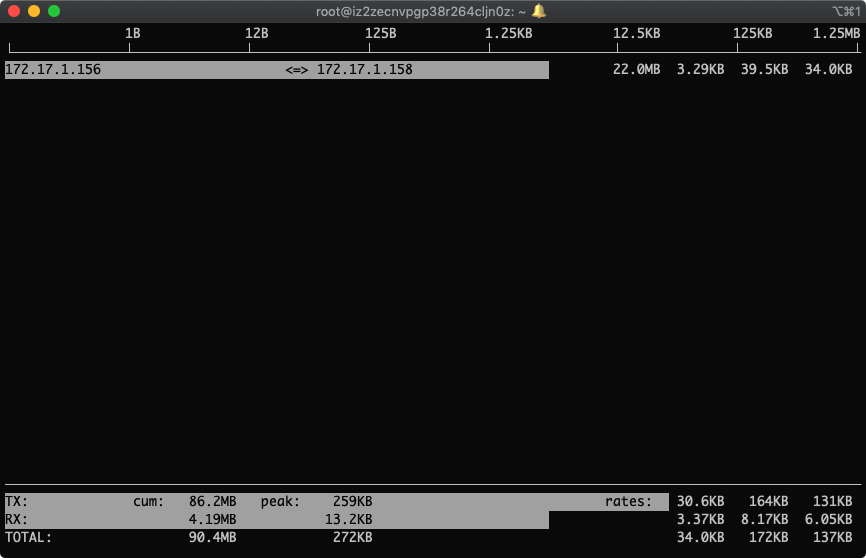
这下就只看到这个ip的流量监控了
8.找到这个ip哪个端口流量用得最多
按下p,根据端口号显示
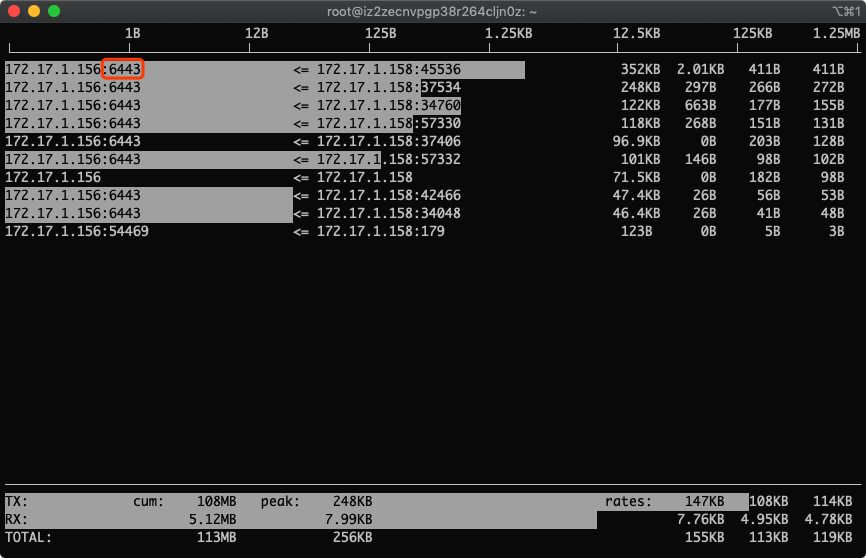
到这里,我们就学会了如何找出流量用得最多的ip和端口号,这么好干货你不high起来对不起哥这么用心的截图!
