余姚网站建设余姚最佳磁力搜索引擎
接上一篇《centos7部署rancher2.5详细图文教程》
一、 安装nfs服务
1. 所有节点都需要操作
$ # 下载 nfs 相关软件
$ sudo yum -y install nfs-utils rpcbind$ # 启动服务并加入开机自启
$ sudo systemctl start nfs && systemctl enable nfs
$ sudo systemctl start rpcbind && systemctl enable rpcbind
2. 配置存储节点(这里选master机器)
$ # 创建共享目录并赋予最大权限
$ sudo mkdir -p /data/rancher_nfs && chmod -R 777 /data/rancher_nfs#$ # 多种权限配置策略,此处举例两种,第一种为限制 172.20.29.* 网段访问
#$ sudo echo "/data/rancher_nfs 172.20.29.*(rw,no_root_squash,no_all_squash,sync)" >> /etc/exports
$ # 第二种为无限制访问
$ sudo echo "/data/rancher_nfs *(rw,no_root_squash,no_all_squash,sync)" >> /etc/exports# 配置完成后重新加载
$ sudo exportfs -r
$ # 查看挂载点信息
$ sudo showmount -e
二、 配置nfs服务
1. 进入到目标集群
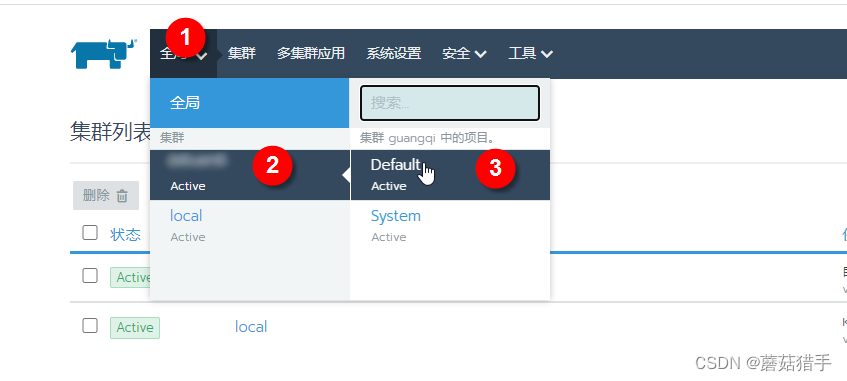
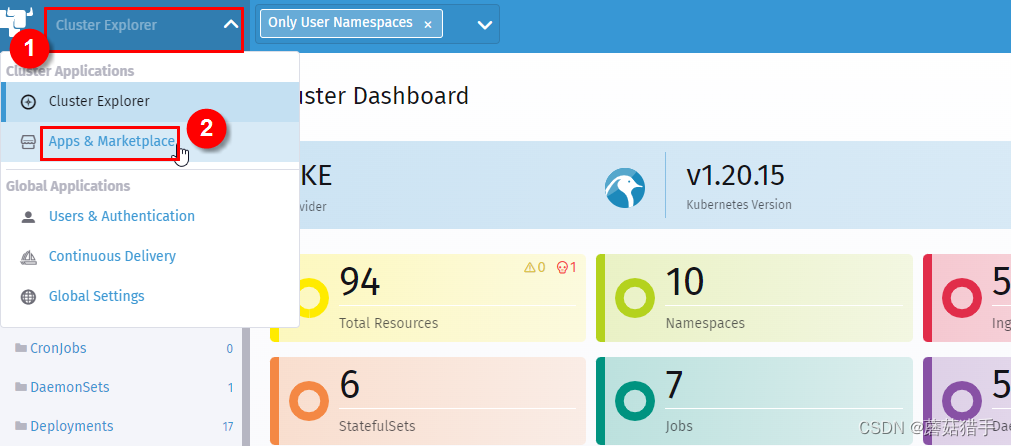
2. 进入该集群的仪表盘(Cluster Explorer)

3. 进入Apps & Marketplace(应用市场)
右下角可切换中英文,这里以进来后默认的英文继续
4. 添加Chart Repositories(Chart仓库)
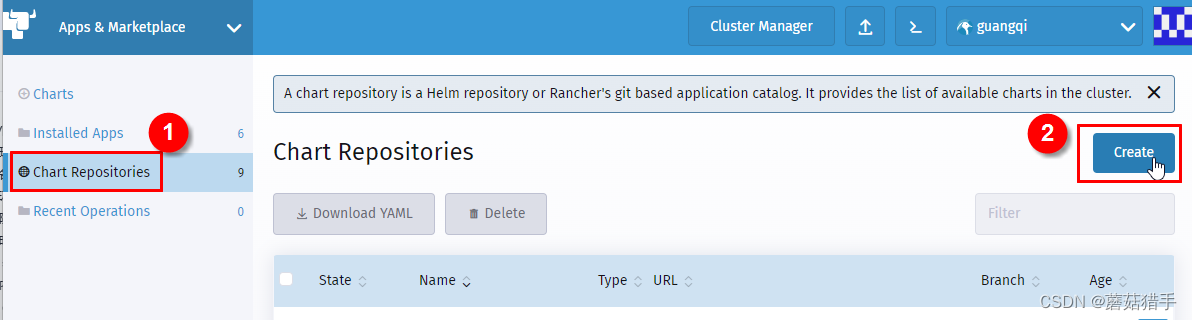
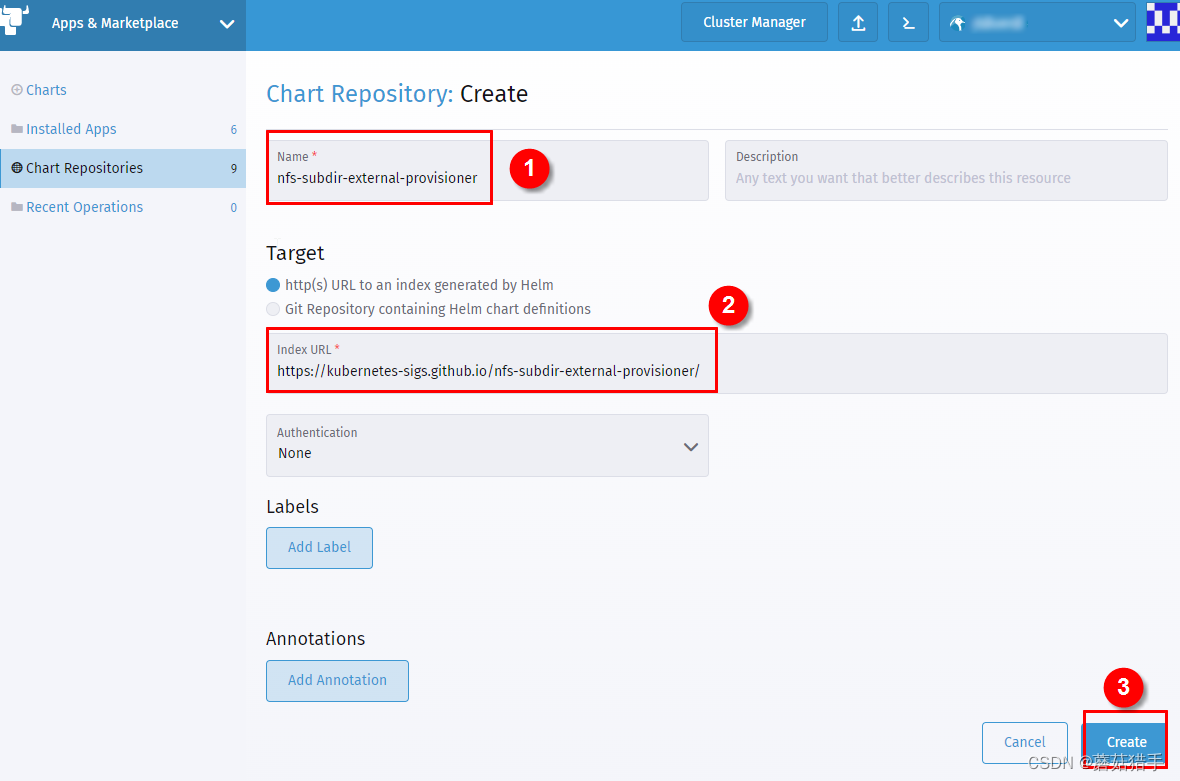
5. 填写仓库信息
名称:nfs-subdir-external-provisioner
Index URL:https://kubernetes-sigs.github.io/nfs-subdir-external-provisioner/
注意URL不要有空格
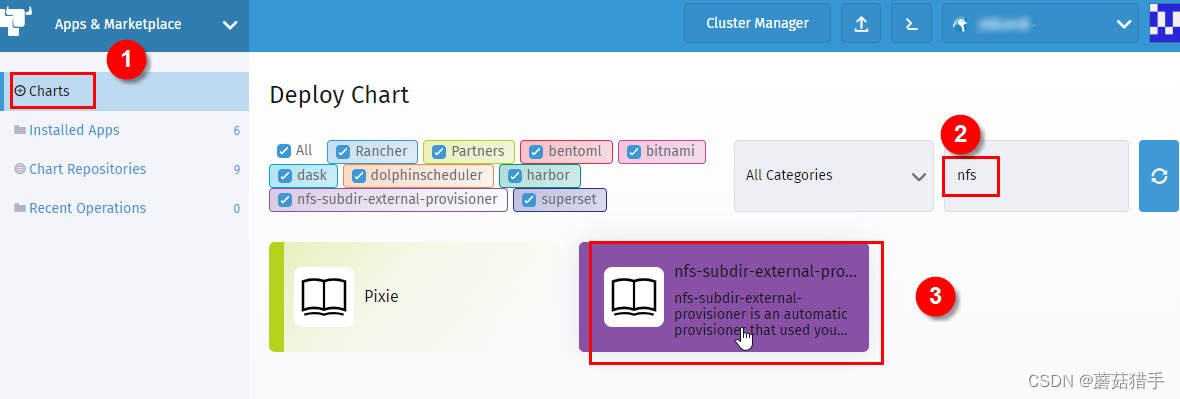
6. 安装nfs-subdir-external-provisioner
7. 配置nfs-subdir-external-provisioner
path和server的值即为选定的用来持久化的机器IP和路径
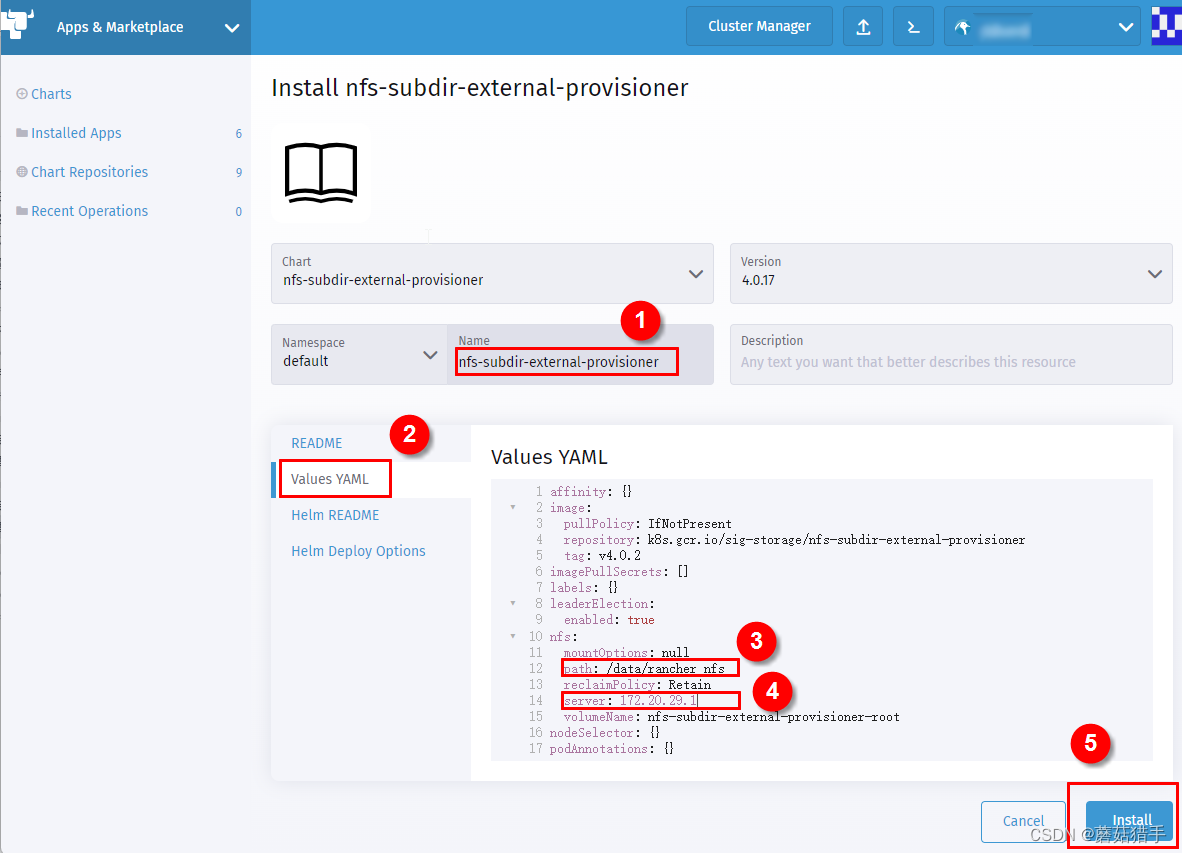
这里需要注意,点击install等一段时间后,可能会发现安装失败,这是因为相关的镜像拉取失败,返回rancher UI进入集群的工作负载中查看,就会看到如下的报错
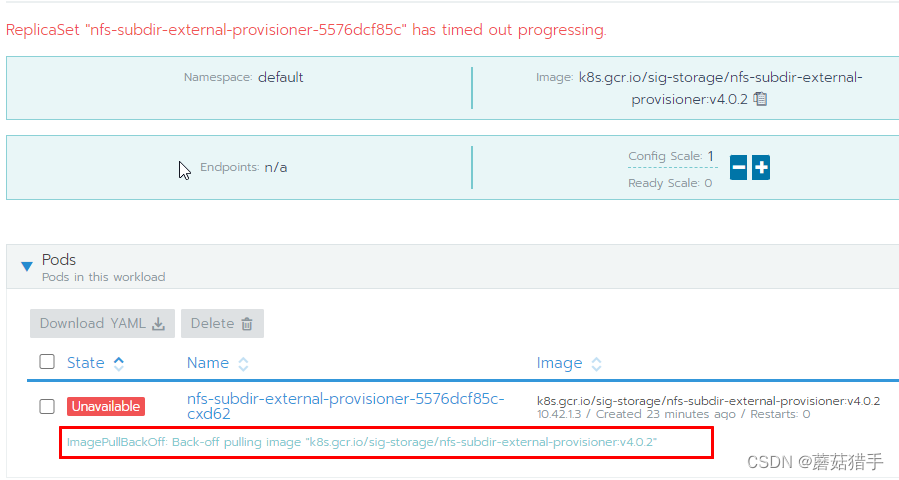 可以多从网上搜搜该镜像,找到下载后,导入到k8s的每一台机器中(实在搞不定的话,可以留言,我看到后发给你)。
可以多从网上搜搜该镜像,找到下载后,导入到k8s的每一台机器中(实在搞不定的话,可以留言,我看到后发给你)。
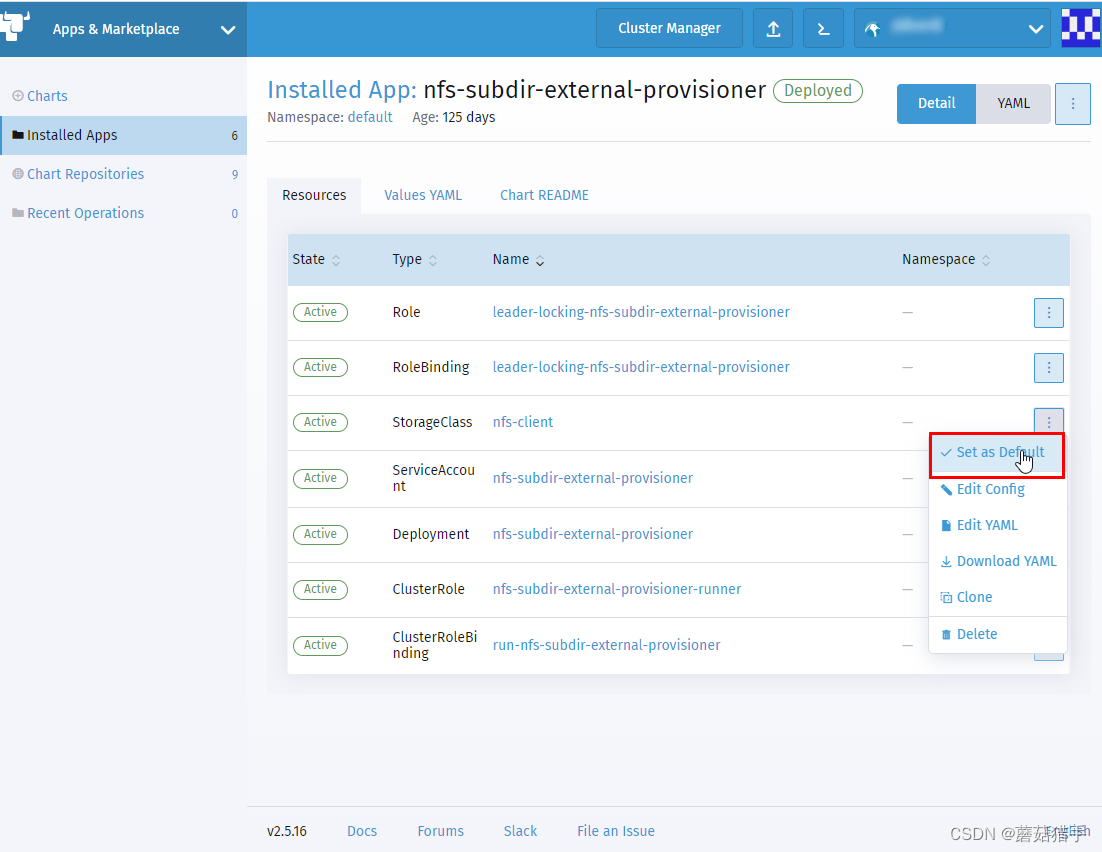
8. 安装好后,将其设为默认存储