网站建设工作半年通报360seo排名点击软件
Kafka
Kafka 是一个分布式的基于发布/订阅模式的消息队列(Message Queue),主要应用于大数据实时处理领域。
Kafka可以用作Flink应用程序的数据源。Flink可以轻松地从一个或多个Kafka主题中消费数据流。这意味着您可以使用Kafka来捕获和传输实时数据,并将其发送到Flink进行进一步处理。
Flink和Kafka在实时数据处理和流处理应用程序中通常协同工作,Kafka用于数据传输和捕获,而Flink用于数据处理和分析。
Kafka由 生产者 Broker 消费者组成,生产者和消费者是由Java语言编写的,Broker由Scala语言写的。
基础架构
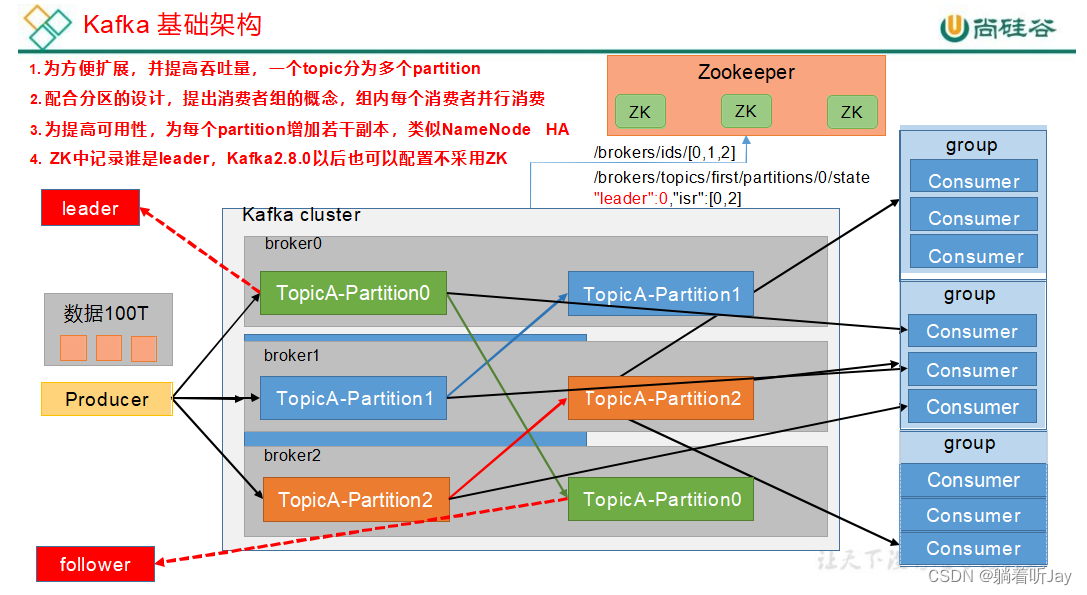
- Producer:kafka 生产者,用于接收外部数据,然后将数据发送给kafka集群存储,假如要发100T的数据。
- Consumer:消费者,就是到kafka中取数据的客户端,比如:flink就是一个消费者,到kafka中取出数据计算处理。
- Broker:一个Broker就是一个kafka服务器,如果你在一个虚拟机上安装了kafka,那么这个虚拟机就是一个Broker。
- Partition:分区。前面说了,要发送100T的数据给kafka,那如果只用一台kafka服务器(Broker)接收肯定不好,太大了。所以就有了kafka集群一起处理,这100T的数据是一个主题,太大了,就考虑分区,分成3个区,每个分区分到不同的kafka服务器上,一个分区存33T。
- Consumer Group:消费者组。由多个消费者组成,消费者就是来取kafka中的数据来处理使用的。现在kafka已经存储了100T的数据,假如一个消费者来取使用,肯定比较慢,所以就可以引入多个消费者一起来取数据处理。一个分区中的数据只能由一个消费者
- Replica:副本。每个分区可以设置一个或多个副本,我理解是副本会同步主分区中的数据,假如主分区挂了,副本就可以顶上去了。
- Leader:领导。主分区,所有副本分区中的主分区,生产者和消费者都只操作主分区。
- Follower:除了主分区,其他的副本分区都是Follower,Follower会从Leader中同步数据,当Leader挂了,某个Follower会成为新的Leader。
- zookeeeper: ZooKeeper 用于协调和管理 Kafka 集群的各个组件,包括 Broker、Topic 配置、分区分配、Leader 选举等。Kafka 使用 ZooKeeper 来维护集群的整体状态和配置信息,以确保各个组件之间的协同工作。
生产者
在消息发送的过程中,涉及到了两个线程——main 线程和 Sender 线程。在 main 线程中创建了一个双端队列 RecordAccumulator。main 线程将消息发送给 RecordAccumulator, Sender 线程不断从RecordAccumulator 中拉取消息发送到Kafka Broker。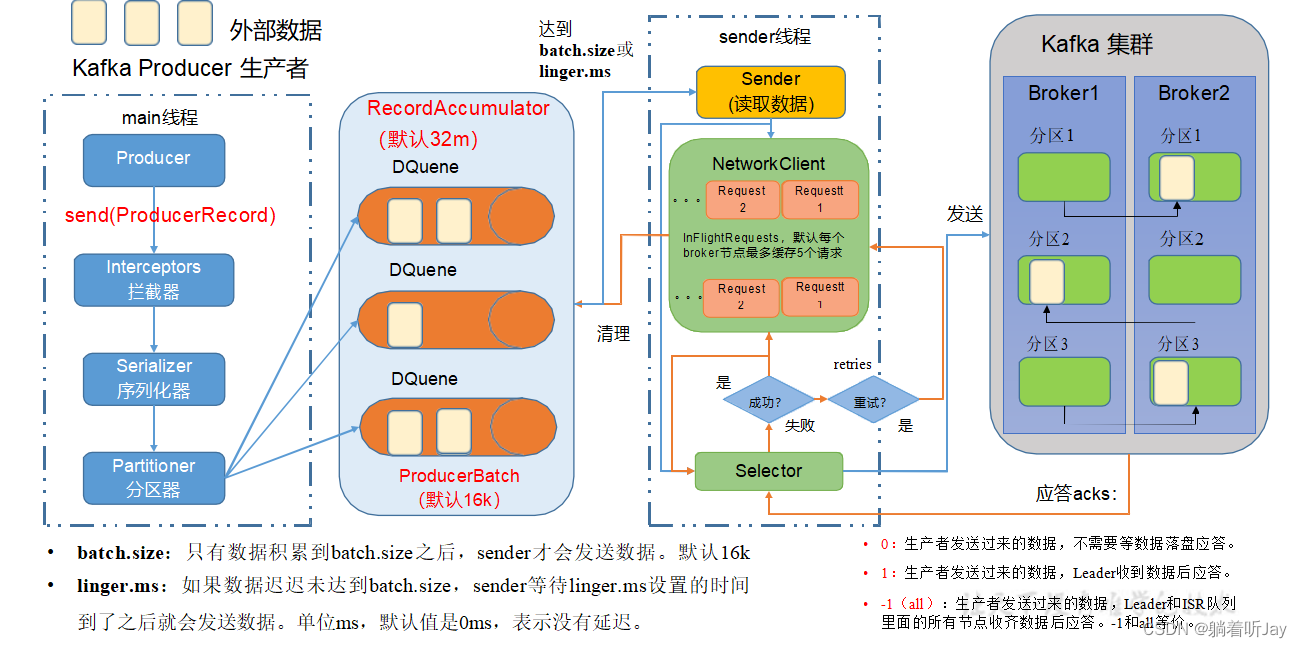
生产者的main线程
main线程先创建Producer对象,然后调用send方法,数据会经过拦截器,进行过滤处理,如果不需要可以不设置拦截器,拦截器用的较少。接着经过序列化器对数据进行序列化(在网络中传输数据需要序列化将数据转成通用的字节流便于网络传输),然后经过分区器,分区器决定每条数据要发往哪个分区,然后将每条数据发给对应的分区,一个分区对应一个DQuee(双端队列),队列中会有一批一批数据,一批数据默认大小是16k。
总的来说,main线程将数据发到RecordAccumulator记录累加器中,默认大小是32m,这个是在内存中,起到缓存的作用,将大量的数据一批一批发给kafka,提高网络传输速率。累加器使用有限的内存,当内存耗尽时(生成者产生数据的速度超过发送给服务器的速度),追加调用将阻塞,除非显式禁用此行为。
sender线程,负责将数据发给kafka。数据是分批次发给kafka,当一个批次的数据达到16k或等待的时间达到linger.ms设置的时间,一个批次的数据就会被sender发给kafka,一个批次就是分区队列中那个小正方形。
sender发送数据:broker1(request1,request2,request3,request4,request5),每个kafka节点维护一个发送数据的请求缓存,这个请求缓存最多缓存5个请求,如果请求发送失败了,会使用后面的请求继续发。批数据到达对应的broker后,会先同步副本。
生产者分区
分区好处:
1)便于合理使用存储资源,每个Partition在一个Broker上存储,可以把海量的数据按照分区切割成一
块一块数据存储在多台Broker上。合理控制分区的任务,可以实现负载均衡的效果。
2)提高并行度,生产者可以以分区为单位发送数据;消费者可以以分区为单位进行消费数据。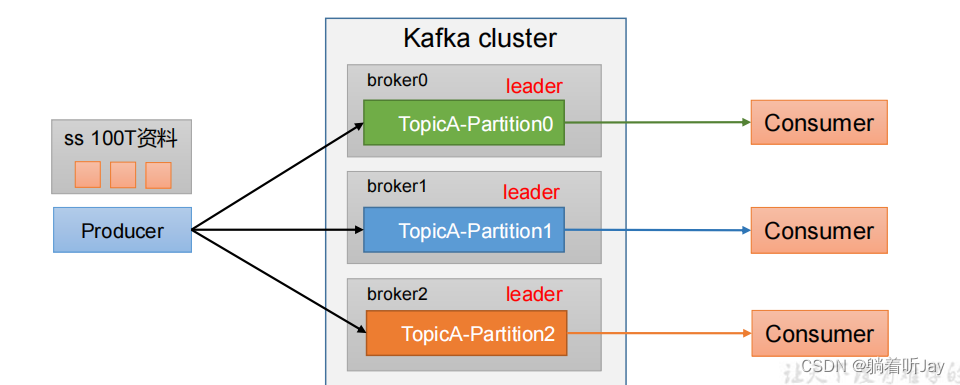
生产者发送消息的分区策略
ProducerRecord是生产者发送数据的单位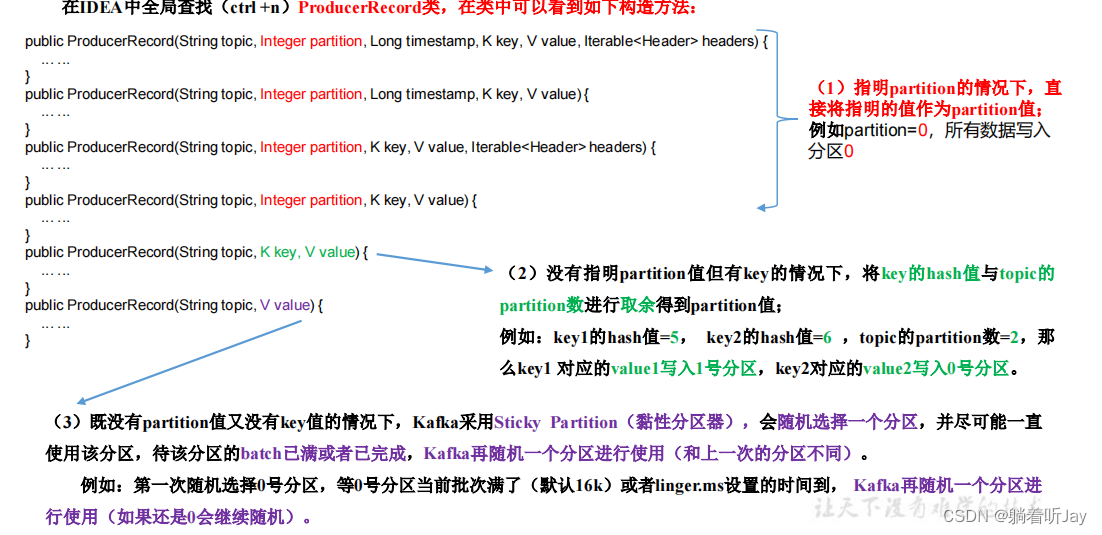
自定义分区器
也可以自定义分区器,自己决定数据要发到哪个分区中
import org.apache.kafka.clients.producer.Partitioner;
import org.apache.kafka.common.Cluster;
import java.util.Map;
/**
发送过来的数据中如果包含 atguigu,就发往 0 号分区,不包含 atguigu,就发往 1 号分区定义类实现 Partitioner 接口,重写 partition()方法。* 1. 实现接口 Partitioner
* 2. 实现 3 个方法:partition,close,configure
* 3. 编写 partition 方法,返回分区号
*/
public class MyPartitioner implements Partitioner {/*** 返回信息对应的分区* @param topic 主题* @param key 消息的 key* @param keyBytes 消息的 key 序列化后的字节数组* @param value 消息的 value* @param valueBytes 消息的 value 序列化后的字节数组* @param cluster 集群元数据可以查看分区信息* @return*/@Overridepublic int partition(String topic, Object key, byte[] keyBytes, Object value, byte[] valueBytes, Cluster cluster) {// 获取消息String msgValue = value.toString();// 创建 partitionint partition;// 判断消息是否包含 atguiguif (msgValue.contains("atguigu")){partition = 0;}else {partition = 1;}// 返回分区号return partition;}// 关闭资源@Overridepublic void close() {}// 配置方法@Overridepublic void configure(Map<String, ?> configs) {}
}
然后在生产者配置里加上自定义分区器
// 添加自定义分区器
properties.put(ProducerConfig.PARTITIONER_CLASS_CONFIG,"com.atguigu.kafka.producer.MyPartitioner");
生产者如何提高吞吐量
如何提高生产者发送数据的速度,主要是调整以下四个参数
• batch.size:批次大小,默认16k • linger.ms:等待时间,修改为5-100ms
默认是0ms,就是数据一到队列中就发给broker,这样的好处就是实时性好,但是效率低,一次发几条数据总比一次发一条效率高。也不能改太大,太大时效性不好。• compression.type:压缩snappy
压缩数据,这样一批次就可以存更多的数据• RecordAccumulator:缓冲区大小,可修改为64m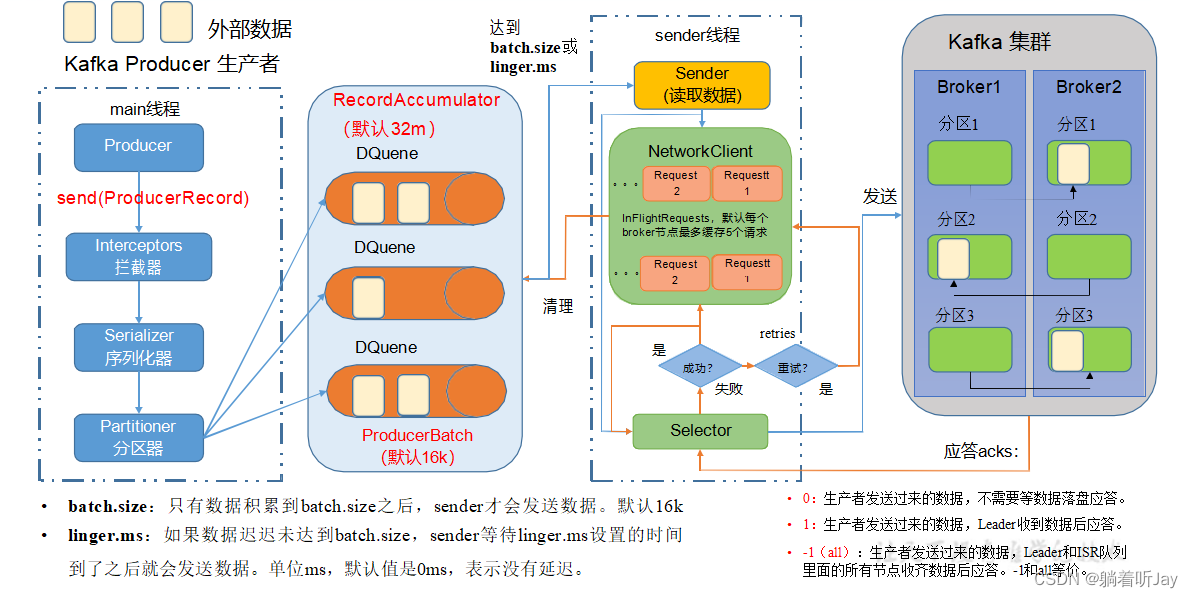
生产者数据可靠性
主要是当broker收到数据后的应答机制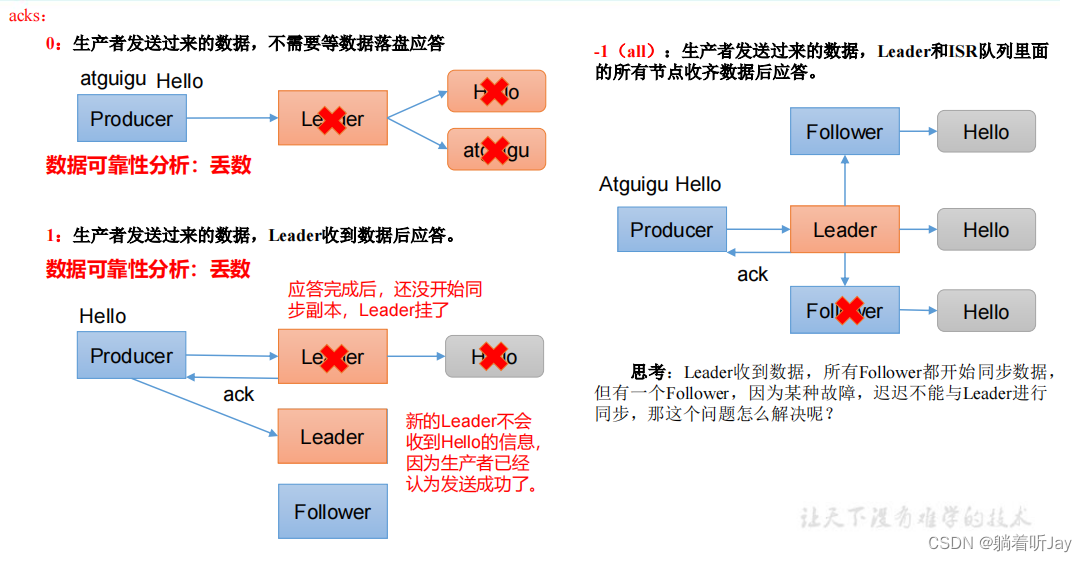
ISR队列是只一个分区的Leader和所有的Followers的集合,ISR(0,1,2),为了解决那个问题,如果Leader长时间没收到某个Follower同步数据的请求,就会认为这个Follower故障了,就会从ISR队列中踢出这个Follower,ISR(0,1)。
如果Follower长时间未向Leader发送通信请求或同步数据,则 该Follower将被踢出ISR。该时间阈值由replica.lag.time.max.ms参 数设定,默认30s。例如2超时,(leader:0, isr:0,1)。
数据完全可靠条件 = ACK级别设置为-1 + 分区副本大于等于2 + ISR里应答的最小副本数量大于等于2
数据可靠性越强,效率越慢

// 设置 acksproperties.put(ProducerConfig.ACKS_CONFIG, "all");// 重试次数 retries,默认是 int 最大值,2147483647properties.put(ProducerConfig.RETRIES_CONFIG, 3);
消费者

消费者消费一个分区中的数据时,会跟踪他们自己消费到的偏移量,Kafka 会定期将偏移量提交到 Kafka 主题中的特殊主题(__consumer_offsets)中,这样,消费者如果停止或重新启动后,会从上次的偏移量继续消费。偏移量是每条消息在分区中的位置。
主题
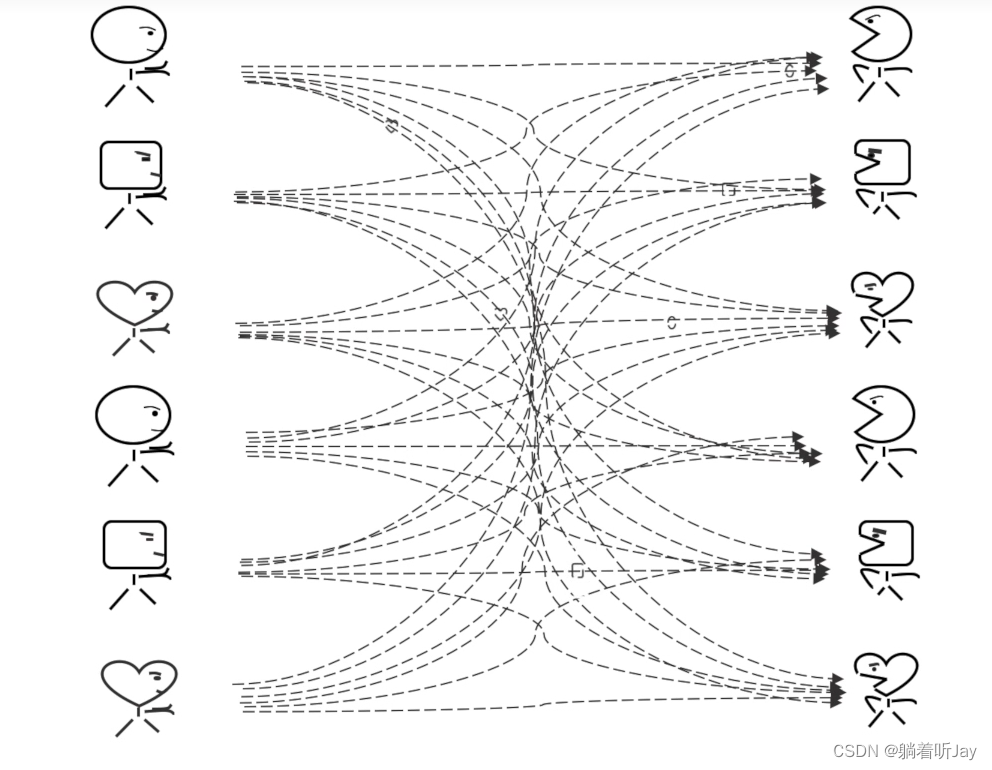
上面那样肯定不好,各种消息的的生产者(生产圆蛋蛋、生产方框框、生产小心心)将消息都发给kafka,然后kafka将消息都分类,每种分类都有相应的主题,然后消费者根据需要订阅相应的主题。就能收到对应的消息。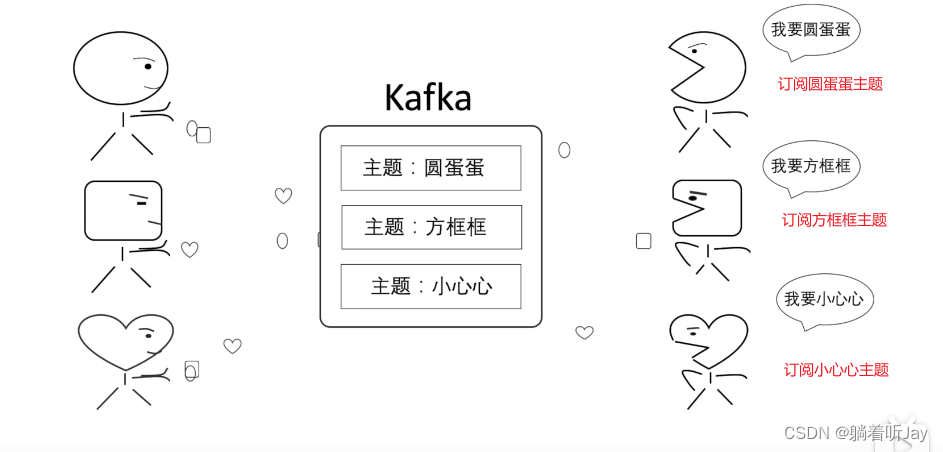
分区
如果一个主题的消息比较多,就可以考虑分区,分区可以分布在不同的服务器上,所以主题也可以分布在不同的服务器上,这样比单服务器处理快。
如果生成者没有指定分区,分区器就会根据每条消息的键算出消息该去哪个分区。键:就是每条消息的一个标记,决定了消息该去哪个分区。分区器:就是一个算法,算消息该去哪个分区,输入是键,输出是消息去的分区。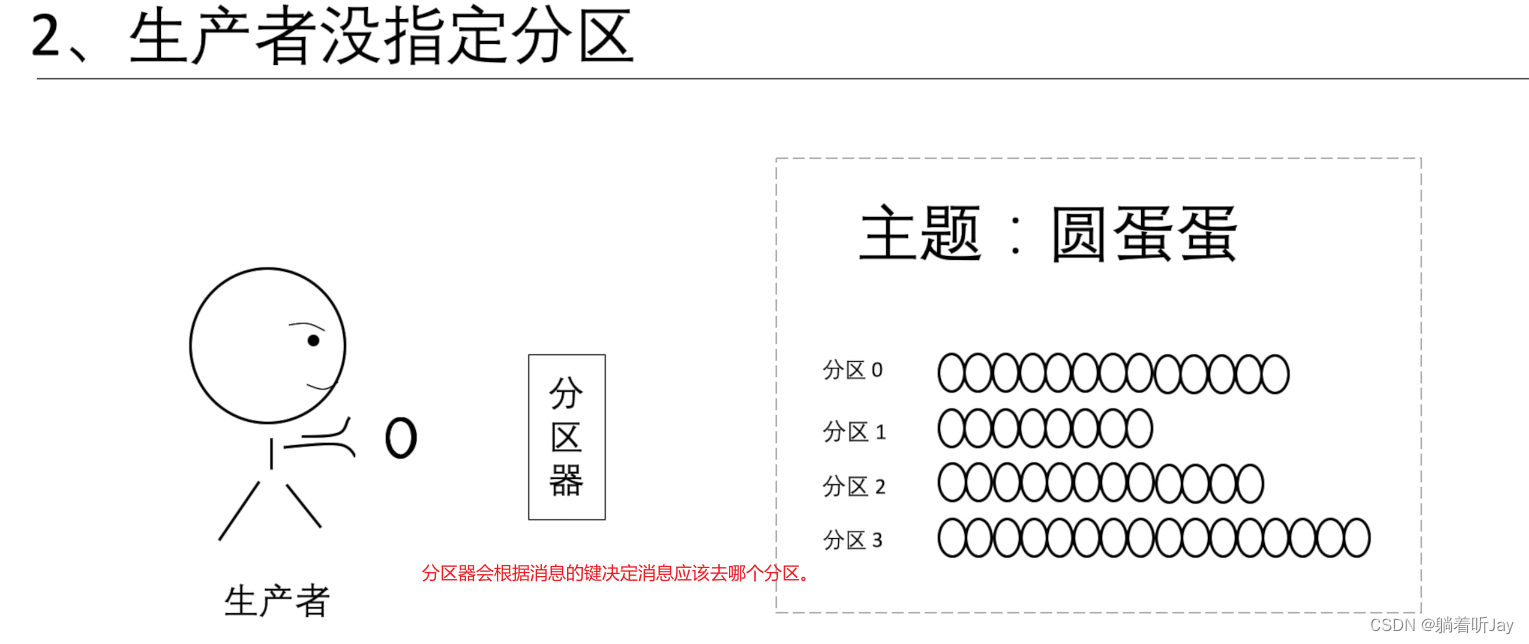
偏移量
偏移量就是消息在每个分区中的位置,kafka在收到消息的时候,会为每个消息设置偏移量,然后将消息存到磁盘中。
消费者只能按顺序消费读取。消费者如果要分区0的第四个,kafka就会说第三个还没读取,不给第四个。
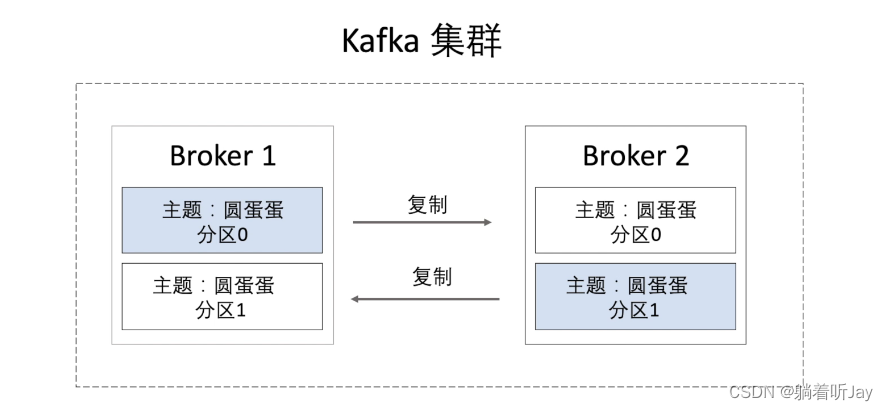
kafka集群
一个broker就是一个kafka服务器。下面有两个broker构成了kafka集群,他们的数据通过复制同步,当有一个kafka宕机了,另一台就可以先顶上,保证了kafka的可靠性。
监控kafka
这个前提得先安装jdk
1、修改kafka的启动脚本
vim bin/kafka-server-start.sh
if [ "x$KAFKA_HEAP_OPTS" = "x" ]; thenexport KAFKA_HEAP_OPTS="-Xmx1G -Xms1G"
fi
改为
if [ "x$KAFKA_HEAP_OPTS" = "x" ]; thenexport KAFKA_HEAP_OPTS="-server -Xms2G -Xmx2G-XX:PermSize=128m -XX:+UseG1GC -XX:MaxGCPauseMillis=200-XX:ParallelGCThreads=8 -XX:ConcGCThreads=5-XX:InitiatingHeapOccupancyPercent=70"export JMX_PORT="9999"#export KAFKA_HEAP_OPTS="-Xmx1G -Xms1G"
fi修改kafka进程信息:
-Xms2G:设置 Kafka 进程的初始堆内存大小为 2 GB。
-Xmx2G:设置 Kafka 进程的最大堆内存大小为 2 GB。
XX:PermSize=128m:设置持久代(PermGen)的初始大小为 128 MB。请注意,这个选项在 Java 8 和更新的版本中不再适用,因为 PermGen 已被 Metaspace 取代。
-XX:+UseG1GC:指定使用 G1 垃圾收集器。
-XX:MaxGCPauseMillis=200:设置最大垃圾收集暂停时间为 200 毫秒。
XX:ParallelGCThreads=8:设置并行垃圾收集线程的数量为 8。
XX:ConcGCThreads=5:设置并发垃圾收集线程的数量为 5。
XX:InitiatingHeapOccupancyPercent=70:设置堆内存占用百分比,当堆内存使用达到 70% 时,启动并发垃圾收集。
这些参数的目的是调整 Kafka 进程的性能和垃圾收集行为,以满足特定的性能需求。请注意,这些参数的值可以根据你的 Kafka 部署和硬件资源进行调整。堆内存的大小和垃圾收集器的选择将影响 Kafka 的性能和稳定性。最后,这段脚本还设置了 JMX 端口为 9999,这是用于监控 Kafka 进程的 Java Management Extensions(JMX)端口。通过此端口,你可以使用 JMX 工具监控 Kafka 进程的性能指标和状态。如果需要监控 Kafka,你可以使用 JMX 工具连接到此端口。
2、官网下载安装包
https://www.kafka-eagle.org/
3、上传解压
第一次解压后,里面有个压缩包再解压才是真正的。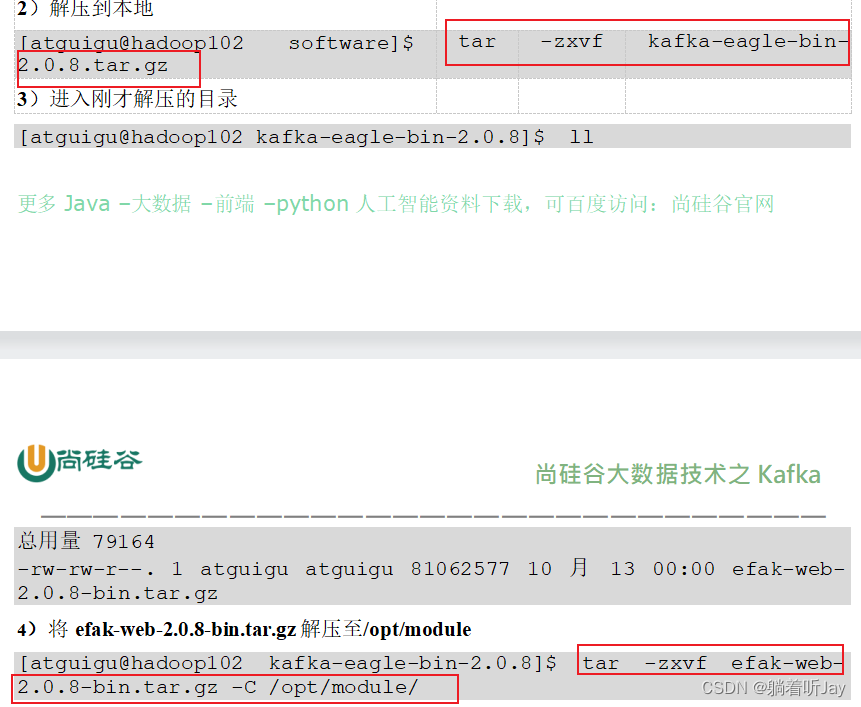
/opt/module/efak/conf/system-config.properties
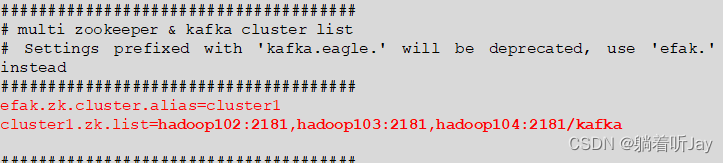

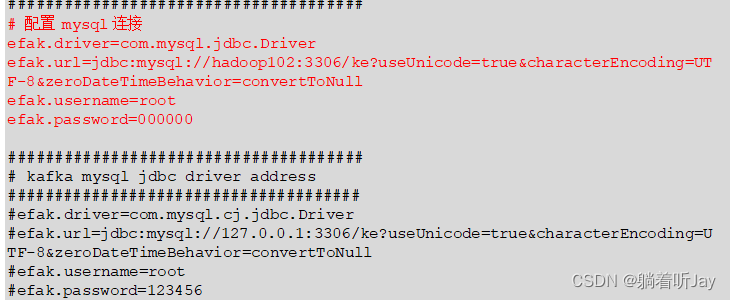
5、配置环境变量
$ sudo vim /etc/profile.d/my_env.sh# kafkaEFAK
export KE_HOME=/opt/module/efak
export PATH=$PATH:$KE_HOME/binsource /etc/profile
6、启动
/bin/kf.sh start
压力测试
# 单Kafka服务器,生成者发送1000000条数据,每条大小1k,总共发送大约
bin/kafka-producer-perf-test.sh --topic test --record-size 1024 --num-records 1000000 --throughput 10000 --producer-props bootstrap.servers=linjl:9092 batch.size=16384 linger.ms=0batch.size=16384 linger.ms=0 9.76 MB/sec
record-size 是一条信息有多大,单位是字节,本次测试设置为 1k。
BUG
1、Error while fetching metadata with correlation id : {LEADER_NOT_AVAILABLE}
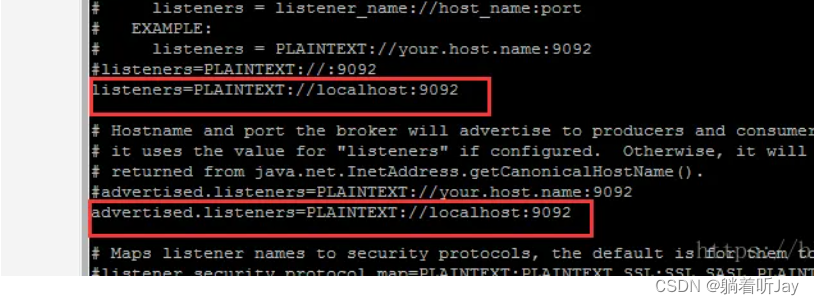
2、
[root@linjl kafka_2.12-3.0.0]# ./bin/kafka-console-consumer.sh --topic quickstart-events --bootstrap-server linjl:9092[2023-09-13 16:51:54,710] WARN [Consumer clientId=consumer-console-consumer-32025-1, groupId=console-consumer-32025] Error while fetching metadata with correlation id 2 : {quickstart-events=LEADER_NOT_AVAILABLE} (org.apache.kafka.clients.NetworkClient)
这个警告消息 “Error while fetching metadata with correlation id 2 : {quickstart-events=LEADER_NOT_AVAILABLE}” 表示 Kafka 消费者在尝试订阅主题 “quickstart-events” 时遇到了 “LEADER_NOT_AVAILABLE” 错误。这个错误通常表示消费者无法找到主题的 leader 分区,因此它无法读取消息。
我的猜想: 可能是因为 Kafka 服务器无法从 ZooKeeper 获取到有关 “quickstart-events” 主题的元数据信息,包括分区的 Leader 信息。
3、Received invalid metadata error in produce request on partition quickstart-events-0
due to org.apache.kafka.common.errors.KafkaStorageException: Disk error when trying to access log file on the disk… Going to request metadata update now (org.apache.kafka.clients.producer.internals.Sender)
表示在尝试将消息写入分区 “quickstart-events-0” 时,Kafka 生产者遇到了磁盘错误,无法访问日志文件。这个错误通常与磁盘故障或磁盘空间不足有关。
4、Java客户端创建生产者,发送消息给kafka没响应。
Properties properties = new Properties();properties.put(ProducerConfig.BOOTSTRAP_SERVERS_CONFIG,"192.168.239.128:9092");// key,value 序列化(必须):key.serializer,value.serializerproperties.put(ProducerConfig.KEY_SERIALIZER_CLASS_CONFIG, StringSerializer.class.getName());properties.put(ProducerConfig.VALUE_SERIALIZER_CLASS_CONFIG, StringSerializer.class.getName())
网络连接都能通,而且防火墙也都关了。
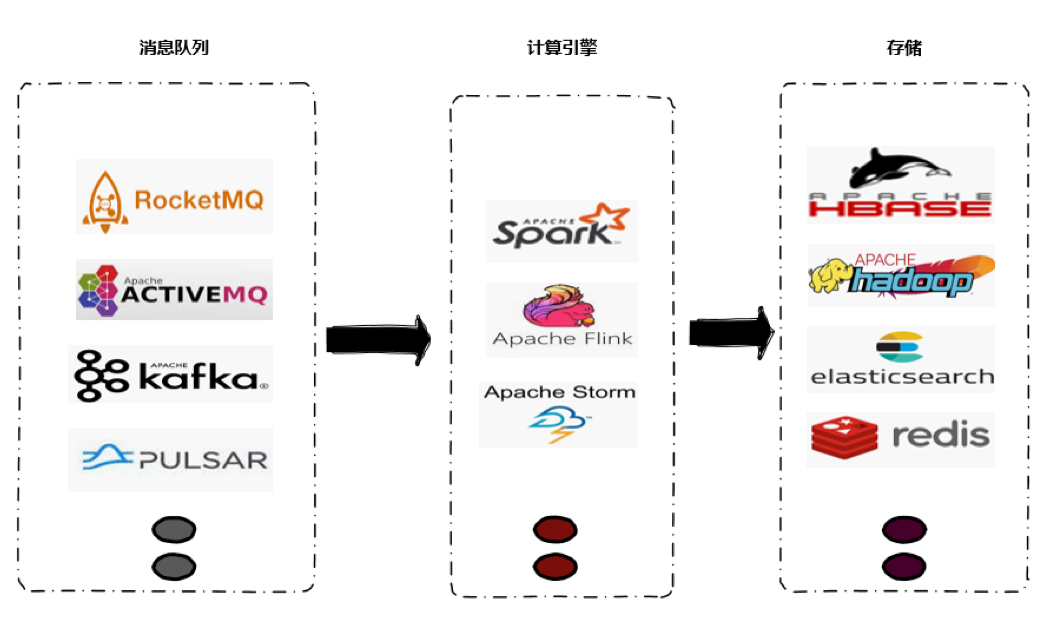
解决:在server.properties配置文件中配置
# The address the socket server listens on. If not configured, the host name will be equal to the value of
# java.net.InetAddress.getCanonicalHostName(), with PLAINTEXT listener name, and port 9092.
# FORMAT:
# listeners = listener_name://host_name:port
# EXAMPLE:
# listeners = PLAINTEXT://your.host.name:9092
listeners=PLAINTEXT://192.168.239.128:9092
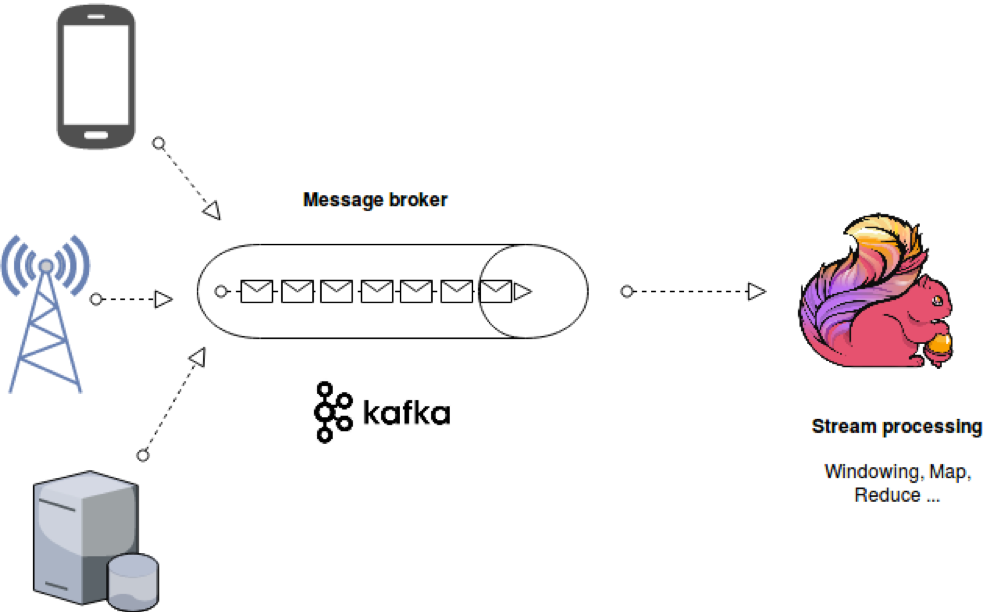
kafka和flink结合案例
数据写入kafka,flink订阅消费
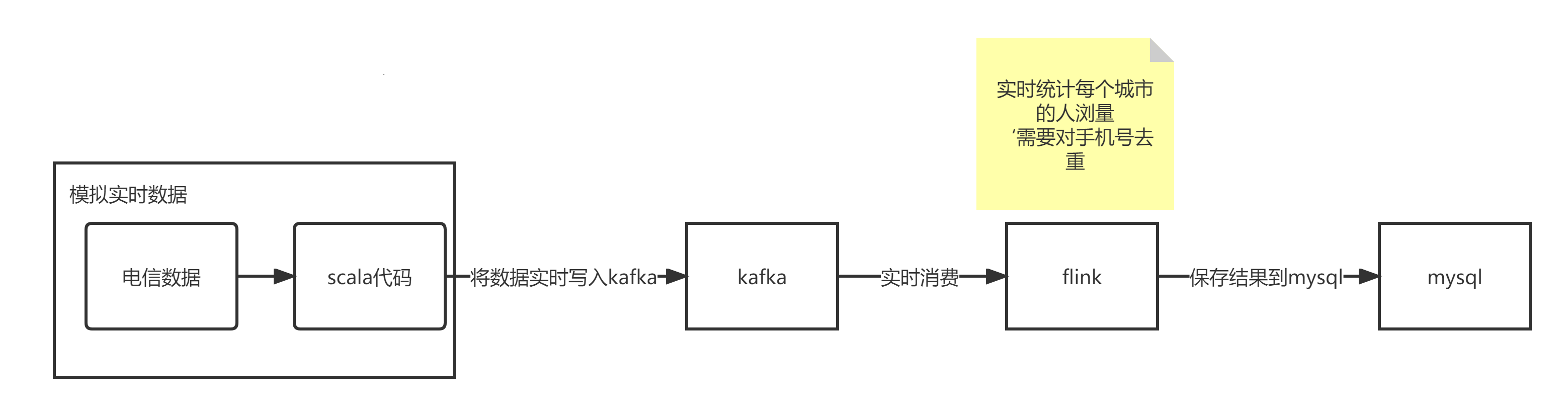
安装kafka单服务
1、官方下载地址:http://kafka.apache.org/downloads.html
2、解压安装包
下载完将安装包上传到centos中,然后解压
$ tar -zxvf kafka_2.12-3.0.0.tgz -C /opt/module/
3、 修改解压后的文件名称
$ mv kafka_2.12-3.0.0/ kafka
4、进入到/opt/module/kafka 目录,修改配置文件
$ cd config/$ vim server.properties
#broker 的全局唯一编号,不能重复,只能是数字。
broker.id=0#处理网络请求的线程数量
num.network.threads=3 #用来处理磁盘 IO 的线程数量
num.io.threads=8#发送套接字的缓冲区大小
socket.send.buffer.bytes=102400 #接收套接字的缓冲区大小
socket.receive.buffer.bytes=102400 #请求套接字的缓冲区大小
socket.request.max.bytes=104857600#kafka 运行日志(数据)存放的路径,路径不需要提前创建,kafka 自动帮你创建,可以配置多个磁盘路径,路径与路径之间可以用","分隔
log.dirs=/opt/module/kafka/datas#topic 在当前 broker 上的分区个数
num.partitions=1#用来恢复和清理 data 下数据的线程数量
num.recovery.threads.per.data.dir=1 # 每个 topic 创建时的副本数,默认时 1 个副本
offsets.topic.replication.factor=1 #segment 文件保留的最长时间,超时将被删除
log.retention.hours=168#每个 segment 文件的大小,默认最大 1G
log.segment.bytes=1073741824# 检查过期数据的时间,默认 5 分钟检查一次是否数据过期
log.retention.check.interval.ms=300000#配置连接Zookeeper 集群地址(在 zk 根目录下创建/kafka,方便管理)
zookeeper.connect=hadoop102:2181,hadoop103:2181,hadoop104:2181/kafka
5、配置kafka环境变量
vim /etc/profile.d/my_env.sh
#KAFKA_HOME
export KAFKA_HOME=/opt/module/kafka
export PATH=$PATH:$KAFKA_HOME/bin
刷新
$ source /etc/profile
6、启动kafka
./kafka/bin/kafka-server-start.sh
创建生产者,将数据写入kafka
