网站架构包括哪些seo网站关键词优化排名
你好,我是 shengjk1,多年大厂经验,努力构建 通俗易懂的、好玩的编程语言教程。 欢迎关注!你会有如下收益:
- 了解大厂经验
- 拥有和大厂相匹配的技术等
希望看什么,评论或者私信告诉我!
文章目录
- 一、前言
- 二、 定义 socket server
- 三、分析客户端请求参数-GET请求
- 四、分析客户端请求参数-PUT请求
- 五、服务端响应参数
- 六、扩展
- 6.1 content-type
- 七、总结
一、前言
上一篇中,我们详细 HTTP 协议的基本原理到请求与响应的详细结构,并且提供了丰富的信息和实用的例子。为了更进一步了解 HTTP 协议,于是有了这篇文章
二、 定义 socket server
本文我们通过 Socket,写一个 HTTP 协议,直观的感受一下上篇文章中的请求和响应。
通过上篇文章,我们知道 HTTP 协议底层是通过 Socket 实现的,所以我们先通过 socket 定义一个 server
import socket#初始化 socke
sock=socket.socket()
#绑定 地址
sock.bind(('127.0.0.1',8081))#在 sock.listen(5) 中,参数 5 表示最多可以排队等待处理的连接数量为 5。
# 如果有更多的连接请求到达,超过该数量的连接将被拒绝。
sock.listen(5)
while True:#接受客户端请求conn,addr=sock.accept()data=conn.recv(1024)print('客户端的请求数据\r\n',data.decode('utf-8'))print("打印完毕=====")#响应客户端的请求conn.send(b'Hello world')conn.close()
在 PyCharm 中执行这段代码后,通过浏览器访问 http://127.0.0.1:8081/
Sever 端 PyCharm 打印结果
客户端的请求数据
GET / HTTP/1.1
Host: 127.0.0.1:8081
Connection: keep-alive
sec-ch-ua: "Chromium";v="122", "Not(A:Brand";v="24", "Google Chrome";v="122"
sec-ch-ua-mobile: ?0
sec-ch-ua-platform: "macOS"
Upgrade-Insecure-Requests: 1
User-Agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7
Sec-Fetch-Site: none
Sec-Fetch-Mode: navigate
Sec-Fetch-User: ?1
Sec-Fetch-Dest: document
Accept-Encoding: gzip, deflate, br, zstd
Accept-Language: en-US,en;q=0.9,zh-CN;q=0.8,zh;q=0.7打印完毕=====
三、分析客户端请求参数-GET请求
在上篇文章中我们讲到 HTTP 协议在发送请求的时候,必须要包含请求行、请求头、请求体。这是浏览器帮我们组织好的。
此处的请求行为
GET / HTTP/1.1
请求头为:
Host: 127.0.0.1:8081
Connection: keep-alive
sec-ch-ua: "Chromium";v="122", "Not(A:Brand";v="24", "Google Chrome";v="122"
sec-ch-ua-mobile: ?0
sec-ch-ua-platform: "macOS"
Upgrade-Insecure-Requests: 1
User-Agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/122.0.0.0 Safari/537.36
Accept: text/html,application/xhtml+xml,application/xml;q=0.9,image/avif,image/webp,image/apng,*/*;q=0.8,application/signed-exchange;v=b3;q=0.7
Sec-Fetch-Site: none
Sec-Fetch-Mode: navigate
Sec-Fetch-User: ?1
Sec-Fetch-Dest: document
Accept-Encoding: gzip, deflate, br, zstd
Accept-Language: en-US,en;q=0.9,zh-CN;q=0.8,zh;q=0.7
请求体为:
之所以为空,是因为 GET 请求没有请求体。
四、分析客户端请求参数-PUT请求
首先通过 python request 包发送 put 请求,因为请求必须要包括请求行、请求头以及请求体,所以 python request 模板会帮我们组织好。
import requestsdata={"username":"test","password":"<PASSWORD>"}
respone=requests.post("http://127.0.0.1:8081",json=data)
print(respone)
Sever 端 PyCharm打印结果
客户端的请求数据
POST / HTTP/1.1
Host: 127.0.0.1:8081
User-Agent: python-requests/2.31.0
Accept-Encoding: gzip, deflate, br, zstd
Accept: */*
Connection: keep-alive
Content-Length: 46
Content-Type: application/json{"username": "test", "password": "<PASSWORD>"}
打印完毕=====
此处的请求行为:
POST / HTTP/1.1
请求头为:
Host: 127.0.0.1:8081
User-Agent: python-requests/2.31.0
Accept-Encoding: gzip, deflate, br, zstd
Accept: */*
Connection: keep-alive
Content-Length: 46
Content-Type: application/json
请求体为:
{"username": "test", "password": "<PASSWORD>"}
五、服务端响应参数
通过浏览器访问 http://127.0.0.1:8081/ 时,虽然 server 端接受到请求了,也给浏览器反回了 hello world 但浏览器仍然报错了

另外当我们通过 python request 发送 put 请求时,同样 server 端接受到请求了,也返回了 hello world 但 request 程序仍然报错了
Traceback (most recent call last):File "/Users/isx/opt/anaconda3/lib/python3.11/site-packages/urllib3/connectionpool.py", line 791, in urlopenresponse = self._make_request(^^^^^^^^^^^^^^^^^^^File "/Users/isx/opt/anaconda3/lib/python3.11/site-packages/urllib3/connectionpool.py", line 537, in _make_requestresponse = conn.getresponse()^^^^^^^^^^^^^^^^^^File "/Users/isx/opt/anaconda3/lib/python3.11/site-packages/urllib3/connection.py", line 461, in getresponsehttplib_response = super().getresponse()^^^^^^^^^^^^^^^^^^^^^File "/Users/isx/opt/anaconda3/lib/python3.11/http/client.py", line 1390, in getresponseresponse.begin()File "/Users/isx/opt/anaconda3/lib/python3.11/http/client.py", line 325, in beginversion, status, reason = self._read_status()^^^^^^^^^^^^^^^^^^^File "/Users/isx/opt/anaconda3/lib/python3.11/http/client.py", line 307, in _read_statusraise BadStatusLine(line)
http.client.BadStatusLine: Hello world
这是为什么?
上篇文章中,我们也讲过,服务端的响应也必须要包括响应行、响应头以及响应体,而我们写的 sever 中代码,赵括响应体,所以浏览器和 python request 包会报错。
#响应客户端的请求
conn.send(b'Hello world')
我们遵循服务端的响应也必须要包括响应行、响应头以及响应体这个要求,改进 server 代码
import socketsock=socket.socket()sock.bind(('127.0.0.1',8081))
#在 sock.listen(5) 中,参数 5 表示最多可以排队等待处理的连接数量为 5。
# 如果有更多的连接请求到达,超过该数量的连接将被拒绝。
sock.listen(5)
while True:conn,addr=sock.accept()data=conn.recv(1024)print('客户端的请求数据\r\n',data.decode('utf-8'))print("打印完毕=====")conn.send(b'HTTP/1.1 200 OK \r\nDate: Tue, 02 Mar 2024 12:00:00 GMT\r\nServer: Apache/2.4.6 (CentOS) OpenSSL/1.0.2k-fips\r\nContent-Type: text/plain\r\nHello world')conn.close()
六、扩展
6.1 content-type
content-type 是请求头以及响应头中最重要的参数,它可以分别告诉客户端和服务端该如何处理请求体或者响应体中的参数。举个例子:
server代码
import socketsock=socket.socket()sock.bind(('127.0.0.1',8081))
#在 sock.listen(5) 中,参数 5 表示最多可以排队等待处理的连接数量为 5。
# 如果有更多的连接请求到达,超过该数量的连接将被拒绝。
sock.listen(5)
while True:conn,addr=sock.accept()data=conn.recv(1024)print('客户端的请求数据\r\n',data.decode('utf-8'))print("打印完毕=====")conn.send(b'HTTP/1.1 200 OK\r\nContent-Type: text/plain\r\n\r\n{"username": "test", "password": "<PASSWORD>"}')conn.close()
为了更好的呈现响应的结果,这个我们借助 postman 工具。当 Content-Type: text/plain,postman 接受服务端返回的数据类型为 text

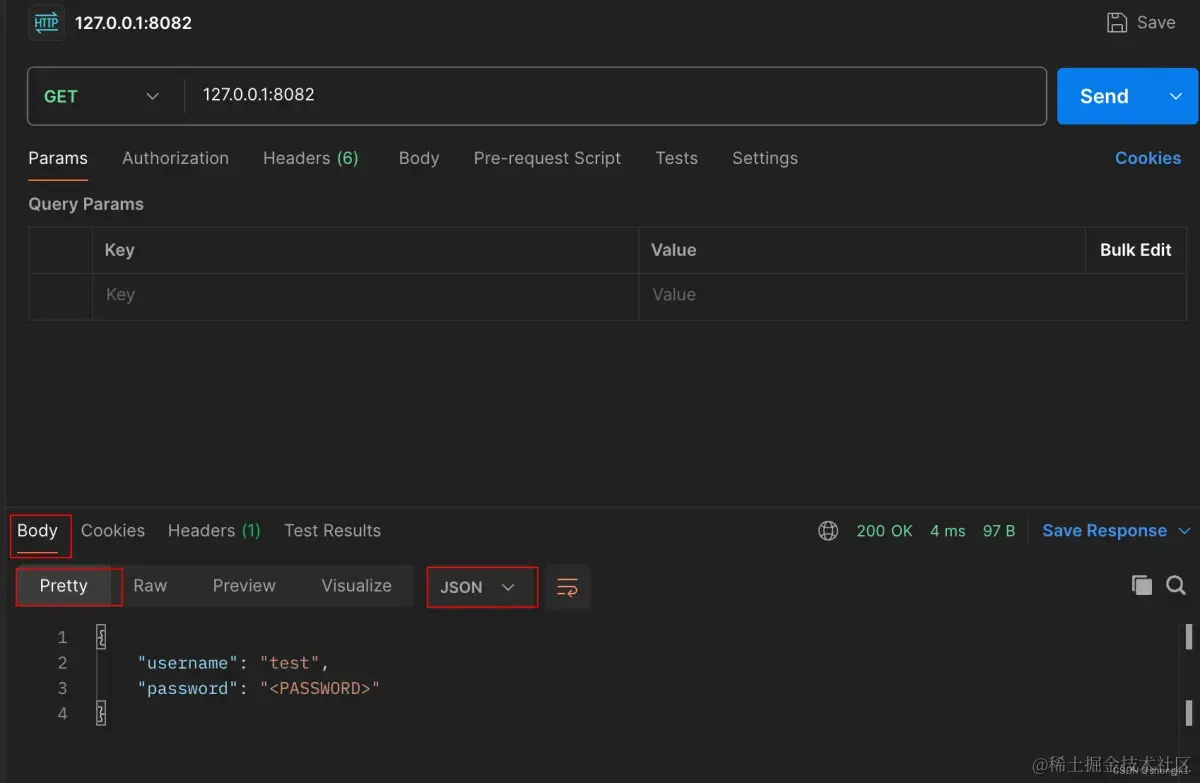
当 Content-Type:application/json 时,postman 服务端返回的数据类型为 json
七、总结
本文通过实际代码和请求示例,深入探讨了HTTP协议的实现和交互过程。通过对Socket的使用,读者能够更直观地理解HTTP请求和响应的过程。同时,文章强调了请求和响应中的参数组成,以及服务端响应中的必要元素。最后,通过content-type的讨论,读者能够更好地理解数据类型对于请求和响应的影响。
