中国500强企业名单seo外链增加
**单片机设计介绍, 基于单片机C51全自动洗衣机仿真设计
文章目录
- 一 概要
- 二、功能设计
- 设计思路
- 三、 软件设计
- 原理图
- 五、 程序
- 六、 文章目录
一 概要
基于单片机C51的全自动洗衣机仿真设计是一个复杂的项目,它涉及到硬件和软件的设计和实现。以下是对这个项目的基本介绍:
设计目标:
全自动洗衣机仿真设计的目标是在单片机C51控制下,实现洗衣机的自动洗衣功能。设计需要考虑的因素包括洗衣机的各种工作状态,如洗涤、漂洗、甩干、烘干等,以及如何通过单片机控制这些状态。
关键技术:
- 单片机C51技术:这是设计的核心,它能够处理洗衣机的各种传感器信号,并发出相应的控制指令。
- 传感器技术:洗衣机需要感知洗衣液浓度、水温、洗涤时间、水位等参数,这就需要用到传感器技术。
- 电源和电机控制技术:洗衣机需要电源供电,同时电机需要控制才能实现洗涤、漂洗、甩干等功能,这就需要用到相应的电源和电机控制技术。
硬件设计:
硬件设计主要包括洗衣机的各个部件和控制器的连接。控制器需要与传感器、电机等部件连接,同时还需要与电源连接。硬件设计需要考虑电器的安全性和可靠性,因此需要使用高质量的元件和合理的布线。
软件设计:
软件设计是全自动洗衣机仿真设计的另一个关键部分。它需要编写程序来控制洗衣机的各个状态,包括洗涤、漂洗、甩干、烘干等。程序需要考虑到各种情况,如传感器信号的异常、电机故障等。此外,还需要编写用户界面,方便用户操作洗衣机。
仿真测试:
在完成硬件和软件的设计后,需要进行仿真测试来验证设计的正确性和可行性。这可以通过在仿真环境中运行程序,并观察洗衣机的各种工作状态来实现。如果有问题需要及时修改和完善设计。
安全和环保:
全自动洗衣机需要考虑安全和环保问题。例如,在设计时需要考虑到过载、过热等情况下的保护措施,同时也要考虑到噪音和污染问题。在设计过程中需要遵循相关安全和环保标准。
总的来说,基于单片机C51的全自动洗衣机仿真设计是一个复杂而重要的项目,需要综合考虑各种因素,包括硬件设计、软件设计、仿真测试、安全和环保等。只有经过充分的考虑和测试,才能设计出高质量的全自动洗衣机。
二、功能设计
基于单片机C51全自动洗衣机仿真设计,包含的功能是非常的完善,进水、浸泡、洗涤、脱水、进水、漂洗、检测液位。
//process: 1浸泡,2脱水,3洗涤,4进水,5漂洗,
//method:1方式一,2方式二,3方式三,4方式四
//speed:1速度1/4,2速度2/4,3速度3/4,4速度4/4
设计思路
设计思路
文献研究法:搜集整理相关单片机系统相关研究资料,认真阅读文献,为研究做准备;
调查研究法:通过调查、分析、具体试用等方法,发现单片机系统的现状、存在问题和解决办法;
比较分析法:比较不同系统的具体原理,以及同一类传感器性能的区别,分析系统的研究现状与发展前景;
软硬件设计法:通过软硬件设计实现具体硬件实物,最后测试各项功能是否满足要求。
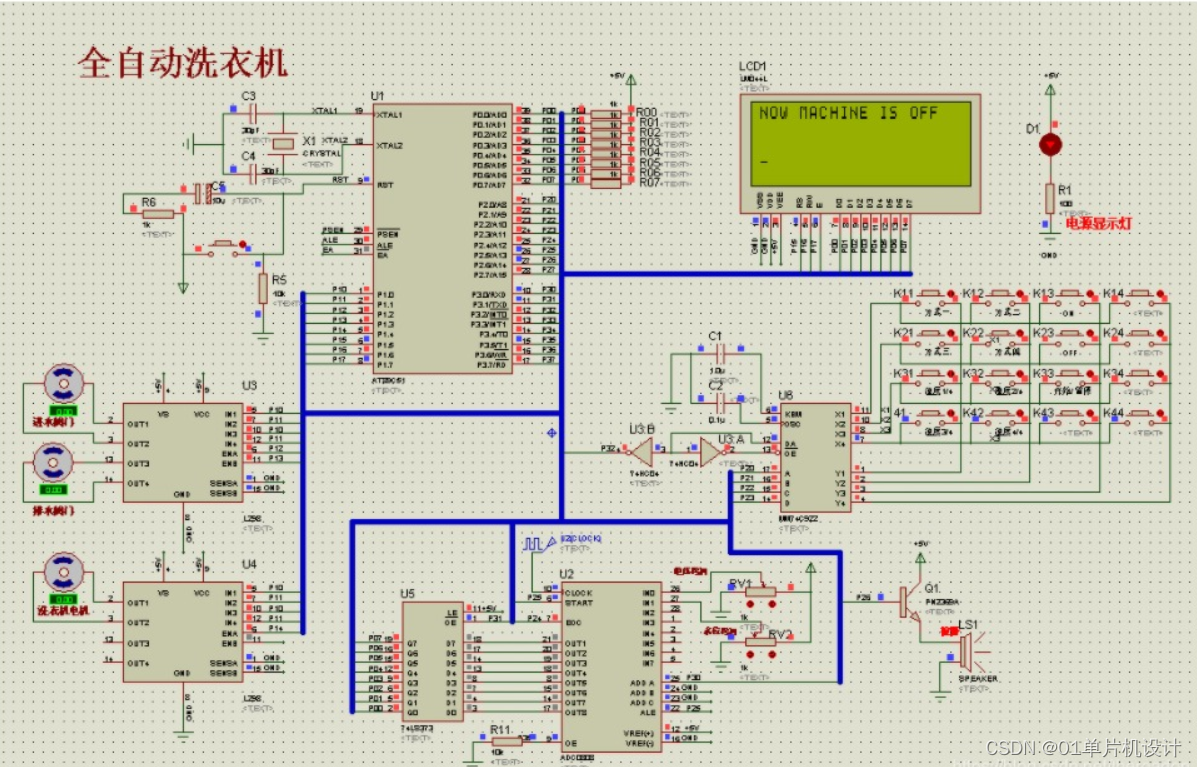
三、 软件设计
本系统原理图设计采用Altium Designer19,具体如图。在本科单片机设计中,设计电路使用的软件一般是Altium Designer或proteus,由于Altium Designer功能强大,可以设计硬件电路的原理图、PCB图,且界面简单,易操作,上手快。Altium Designer19是一款专业的整的端到端电子印刷电路板设计环境,用于电子印刷电路板设计。它结合了原理图设计、PCB设计、多种管理及仿真技术,能够很好的满足本次设计需求。
————————————————
仿真实现
本设计利用protues8.7软件实现仿真设计,具体如图。
Protues也是在单片机仿真设计中常用的设计软件之一,通过设计出硬件电路图,及写入驱动程序,就能在不实现硬件的情况进行电路调试。另外,protues还能实现PCB的设计,在仿真中也可以与KEIL实现联调,便于程序的调试,且支持多种平台,使用简单便捷。
————————————————
原理图
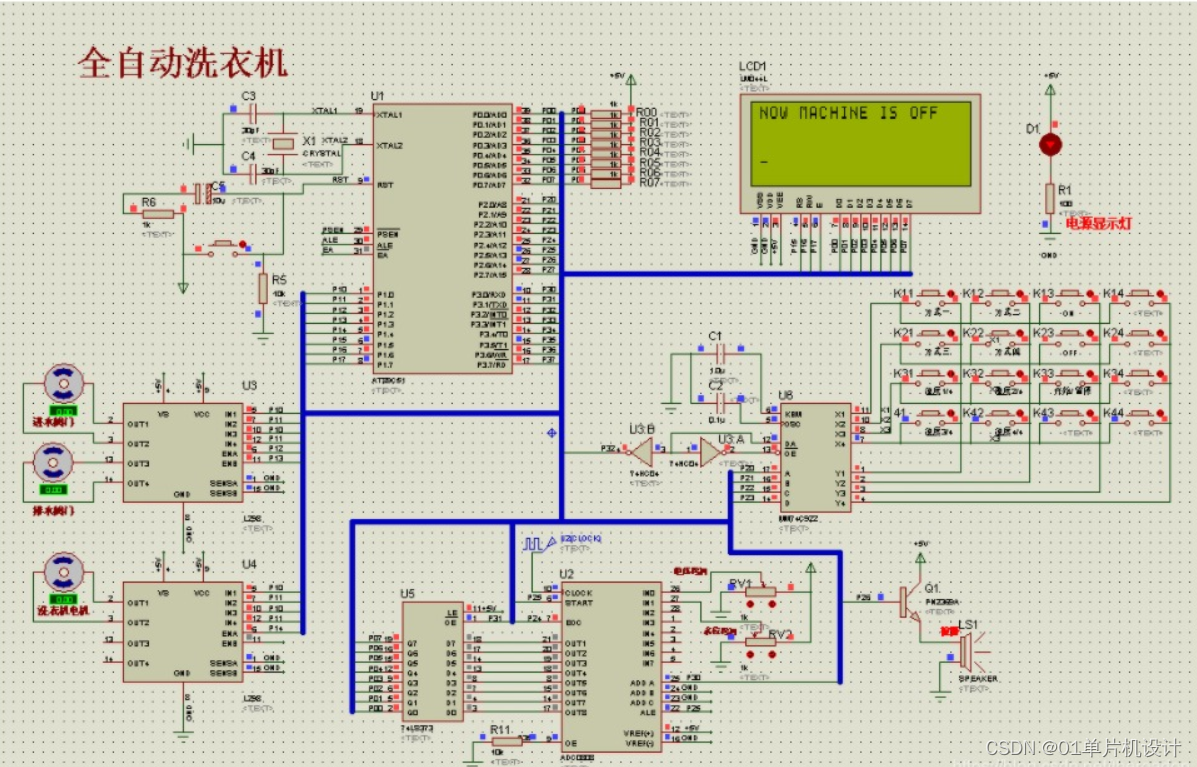
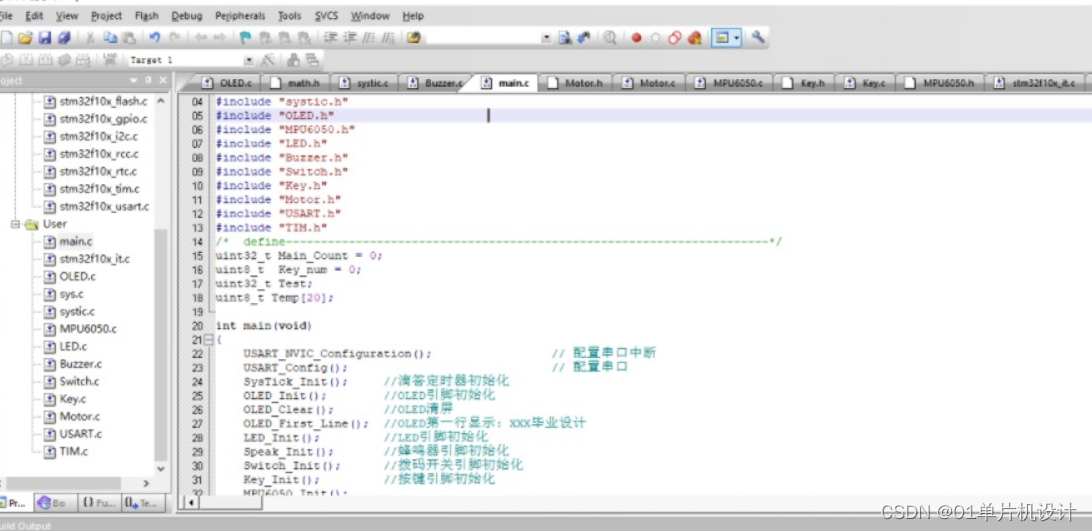
五、 程序
本设计利用KEIL5软件实现程序设计,具体如图。作为本科期间学习的第一门编程语言,C语言是我们最熟悉的编程语言之一。当然,由于其功能强大,C语言是当前世界上使用最广泛、最受欢迎的编程语言。在单片机设计中,C语言已经逐步完全取代汇编语言,因为相比于汇编语言,C语言编译与运行、调试十分方便,且可移植性高,可读性好,便于烧录与写入硬件系统,因此C语言被广泛应用在单片机设计中。keil软件由于其兼容单片机的设计,能够实现快速调试,并生成烧录文件,被广泛应用于C语言的编写和单片机的设计。
————————————————

六、 文章目录
目 录
摘 要 I
Abstract II
引 言 1
1 控制系统设计 2
1.1 主控系统方案设计 2
1.2 传感器方案设计 3
1.3 系统工作原理 5
2 硬件设计 6
2.1 主电路 6
2.1.1 单片机的选择 6
2.2 驱动电路 8
2.2.1 比较器的介绍 8
2.3放大电路 8
2.4最小系统 11
3 软件设计 13
3.1编程语言的选择 13
4 系统调试 16
4.1 系统硬件调试 16
4.2 系统软件调试 16
结 论 17
参考文献 18
附录1 总体原理图设计 20
附录2 源程序清单 21
致 谢 25
