中国建设银行官方网站诚聘英才电子商务

欢迎来到Cefler的博客😁
🕌博客主页:那个传说中的man的主页
🏠个人专栏:题目解析
🌎推荐文章:题目大解析2

目录
- 👉🏻类的默认6个成员函数
- 👉🏻构造函数
- 内置类型和自定义类型与默认构造函数的关系
- 缺省参数和构造函数的配合
- 👉🏻析构函数
👉🏻类的默认6个成员函数
实际上,我们在声明一个类的时候,编译器会默认生成6个成员函数。
默认成员函数:用户没有显式实现(即自己主动写),编译器会生成的成员函数称为默认成员函数。
👉🏻构造函数
🍳概念
构造函数是一个特殊的成员函数,名字与类名相同,创建类类型对象时由编译器自动调用,以保证每个数据成员都有 一个合适的初始值,并且在对象整个生命周期内只调用一次。
🍳特性
构造函数的任务就是用来初始化成员变量
- ⚡️名字和类名相同
- ⚡️无返回值
- ⚡️在实例化对象时自动调用
- ⚡️允许函数重载
class Date{public:Date()//无参构造函数{_year = 1;_month = 1;_day = 1;}Date(int year,int month,int day)//有参构造函数{_year = year;_month = month;_day = day;}private:int _year;int _month;int _day;};int main(){Date d1;Date d2(2023, 8, 5);return 0;}
这里注意,如果是设置无参构造函数,实例化对象,对象不能单单只给一个().
因为编译器不知道你是声明函数还是声明变量。
- ⚡️如果类中没有显式定义构造函数,则C++编译器会自动生成一个无参的默认构造函数,一旦用户显式定义编译器将不再生成。
内置类型和自定义类型与默认构造函数的关系
首先我们先了解下内置类型和自定义类型
内置类型:诸如int、char、double等基本类型,指针全部都是内置类型
自定义类型:class、struct 、union……
默认构造函数:类的对象不需要传参就会自动调用的成员函数。
它们和默认构造函数的关系是什么呢?
默认构造函数对内置类型不进行处理;
默认构造函数会对自定义类型成员调用它的构造函数。
我们举个例子👇🏻👇🏻
class A1{public:A1(){a = 1;cout << a << endl;}int a;};class A2{public:int b;A1 a1;};int main(){A2 var;cout << var.b << endl;return 0;}
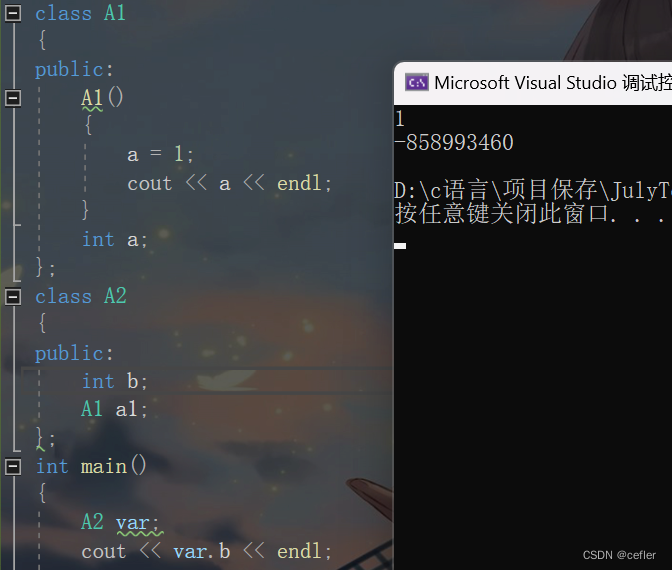
我们可以看到,对于内置类型b,默认构造函数对其没有处理,所以最后的结果是随机值。
但是a1是自定义类型,它在被实例化对象为var时,默认构造函数自动启动,去调用它本身的构造函数,所以它被初始化了。
但是到这里,我们就会发现,如果我们自己不显现一个构造函数,那么内置类型的变量岂不是全都是随机值?
所以在c++11中,为了补这个坑,可以允许内置类型成员变量在类中声明时可以给默认值
缺省参数和构造函数的配合
无参的构造函数和全缺省的构造函数都称为默认构造函数,并且默认构造函数只能有一个。
注意:无参构造函数、全缺省构造函数、我们没写编译器默认生成的构造函数,都可以认为是默认构造函数。
class Date{public:Date()//无参构造函数{_year = 1;_month = 1;_day = 1;}Date(int year = 2023,int month = 8 ,int day = 5)//全缺省构造函数{_year = year;_month = month;_day = day;}private:int _year;int _month;int _day;};
上述中,有无参构造函数和全缺省构造函数。
在语法上是没错的,因为构造函数允许重载。
但是在实例化对象时会出错。
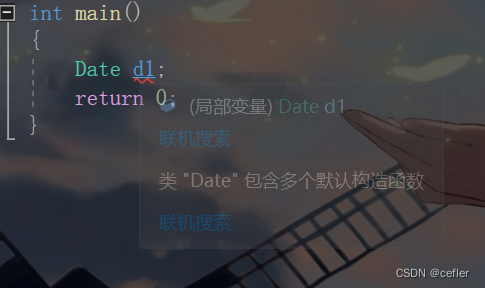
因为出现了两个默认构造函数,所以编译器不知道用哪个。
除非这里给了实参,可以让编译器知道用哪个默认构造函数才不会出问题。
🍽如果这里有一个不是全缺省构造函数,则另一个无参构造函数就是唯一的默认构造函数。
class Date{public:Date()//无参构造函数{_year = 1;_month = 1;_day = 1;}Date(int year ,int month = 8 ,int day = 5)//有参构造函数{_year = year;_month = month;_day = day;}void Print(){cout << _year<<"/" << _month<<"/" << _day << endl;}private:int _year;int _month;int _day;};int main(){Date d1;d1.Print();return 0;}
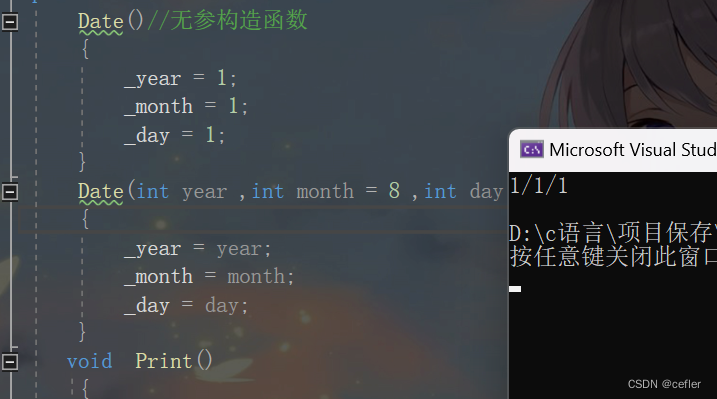
👉🏻析构函数
概念
C++中的析构函数是一种特殊的成员函数,用于在对象被销毁时执行清理操作。析构函数的名称与类名相同,但前面加上一个波浪号(~)。当对象的生命周期结束时(例如,对象超出范围、delete操作符被调用或程序退出),析构函数会自动调用。
析构函数通常是用于释放动态空间上的资源。
特性
- 析构函数名是在类名前加上字符 ~。
- 无参数无返回值类型。
- 一个类只能有一个析构函数。若未显式定义,系统会自动生成默认的析构函数。注意:析构函数不能重载
- 对象生命周期结束时,C++编译系统系统自动调用析构函数。
- 与构造函数类似,对内置类型不处理,但会调用自定义类型成员的默认析构函数
注意:创建哪个类的对象则调用该类的析构函数,销毁那个类的对象则调用该类的析构函数
- 关于编译器自动生成的析构函数,是否会完成一些事情呢?下面的程序我们会看到,编译器生成的默认析构函数,对自定类型成员调用它的析构函数。
class Time
{
public:~Time(){cout << "~Time()" << endl;}
private:int _hour;int _minute;int _second;
};
class Date
{
private:// 基本类型(内置类型)int _year = 1970;int _month = 1;int _day = 1;// 自定义类型Time _t;
};
int main()
{Date d;return 0;
}程序运行结束后输出:~Time()在main方法中根本没有直接创建Time类的对象,为什么最后会调用Time类的析构函数?
因为:main方法中创建了Date对象d,而d中包含4个成员变量,其中_year,_month, _day三个是内置类型成员,销毁时不需要资源清理,最后系统直接将其内存回收即可;
而_t是Time类对象,所以在d销毁时,要将其内部包含的Time类的_t对象销毁,所以要调用Time类的析构函数。
但是:main函数 中不能直接调用Time类的析构函数,实际要释放的是Date类对象,所以编译器会调用Date类的析构函 数,而Date没有显式提供,则编译器会给Date类生成一个默认的析构函数
目的是在其内部调用Time 类的析构函数,即当Date对象销毁时,要保证其内部每个自定义对象都可以正确销毁
main函数中并没有直接调用Time类析构函数,而是显式调用编译器为Date类生的默认析构函数
🖐所以,如果类中没有申请资源(申请动态空间)时,析构函数可以不写,直接使用编译器生成的默认析构函数
