免费网站模块公司网站如何seo
目录
启动JMeter
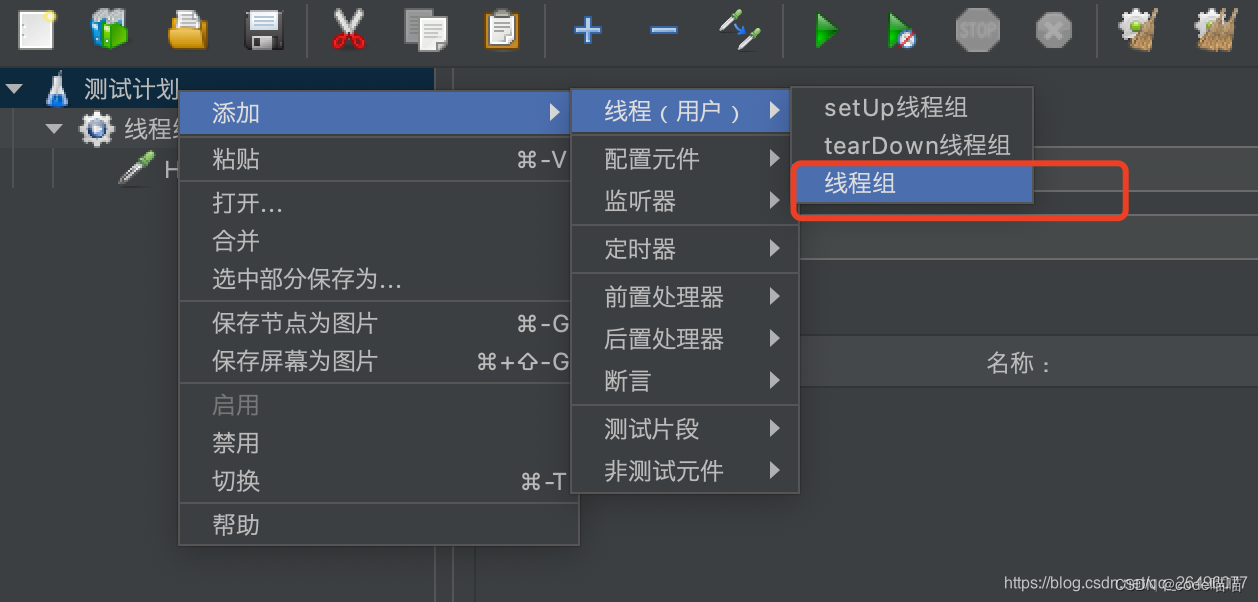
创建线程组
设置线程参数
设置http请求参数
编辑 创建查看结果树(显示成功/失败多少以及返回结果等信息)
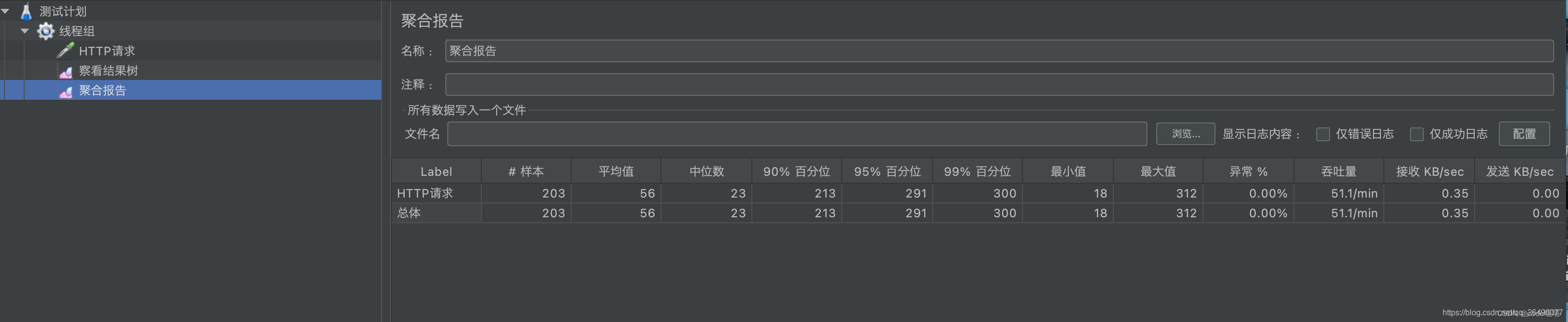
创建聚合报告(显示响应时间、吞吐量、异常数等信息)
点击上方的执行按钮即可开始压力测试
结果树显示
聚合报告结果显示
启动JMeter
在JMeter的bin目录下,执行sh jmeter创建线程组
设置线程参数
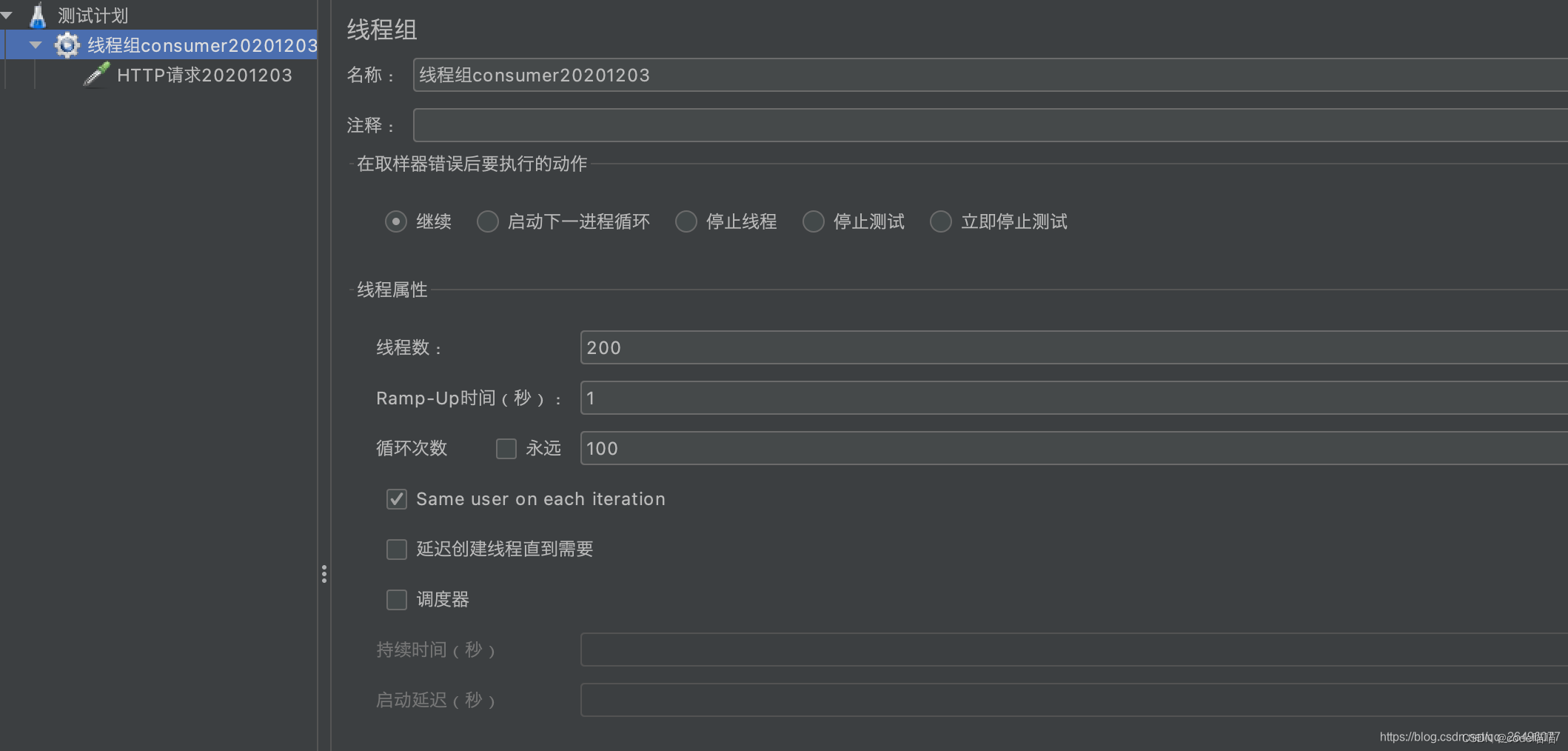
- Ramp-Up为在该时间内发完设置的线程数请求,也就是1s内发完200个线程请求,间隔时间为0.005s
- 循环次数为在几乎同一时刻执行该循环次数的线程请求. 也就是每0.005s发一个线程请求,执行100遍,这100遍的执行时间基本是相同的.即每0.005s发送100次请求,每秒发送200*100=20000次请求.
总结: 在Ramp-Up时间内发送线程数*循环次数个请求
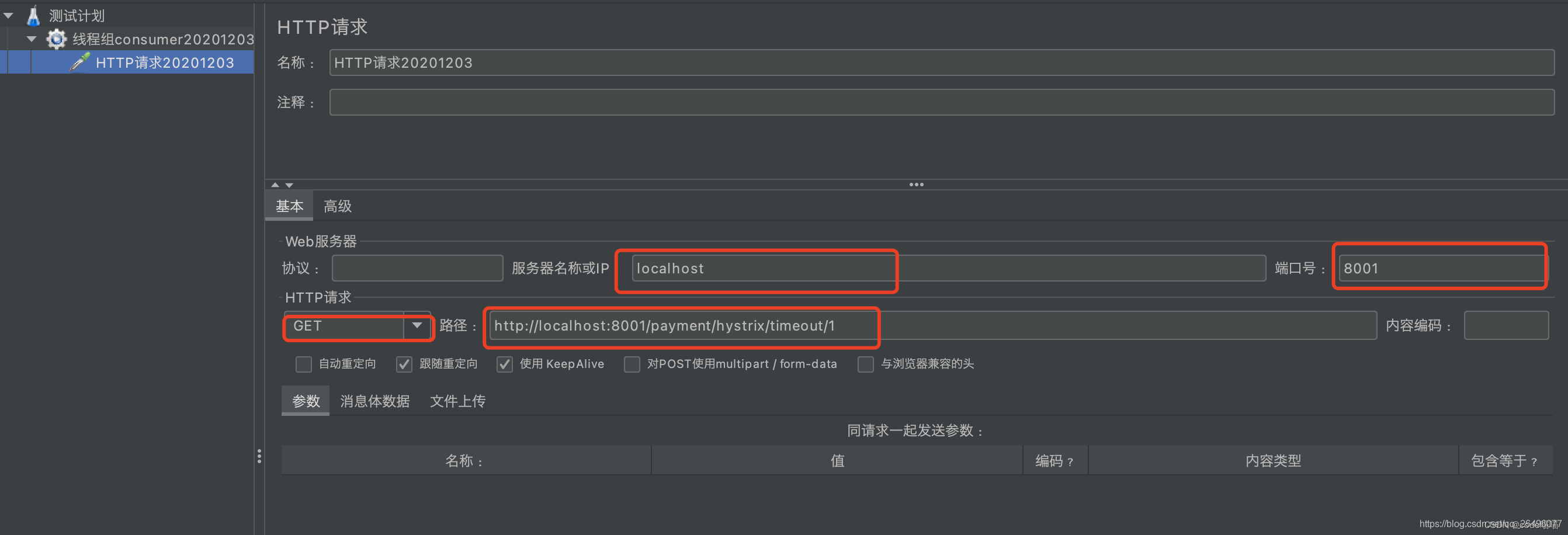
设置http请求参数
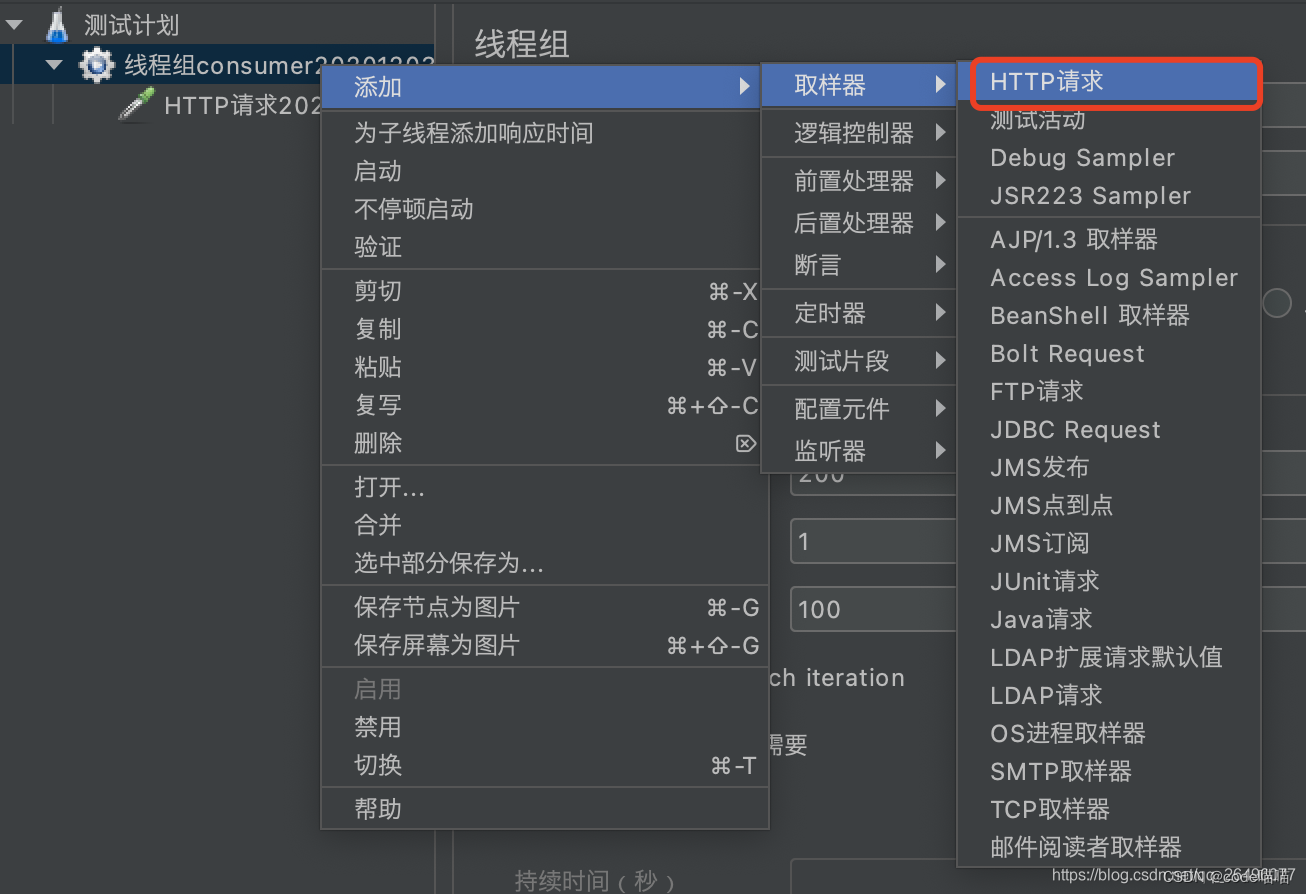
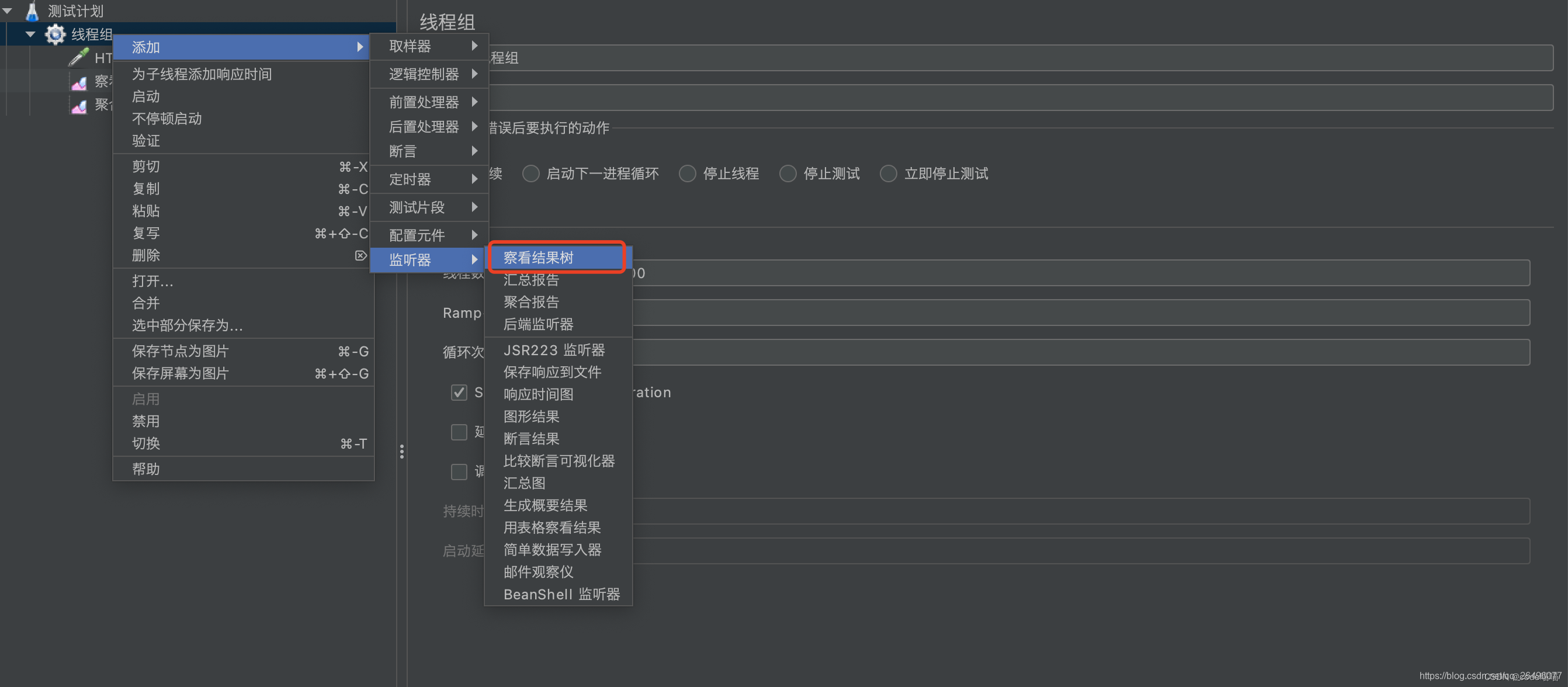
 创建查看结果树(显示成功/失败多少以及返回结果等信息)
创建查看结果树(显示成功/失败多少以及返回结果等信息)
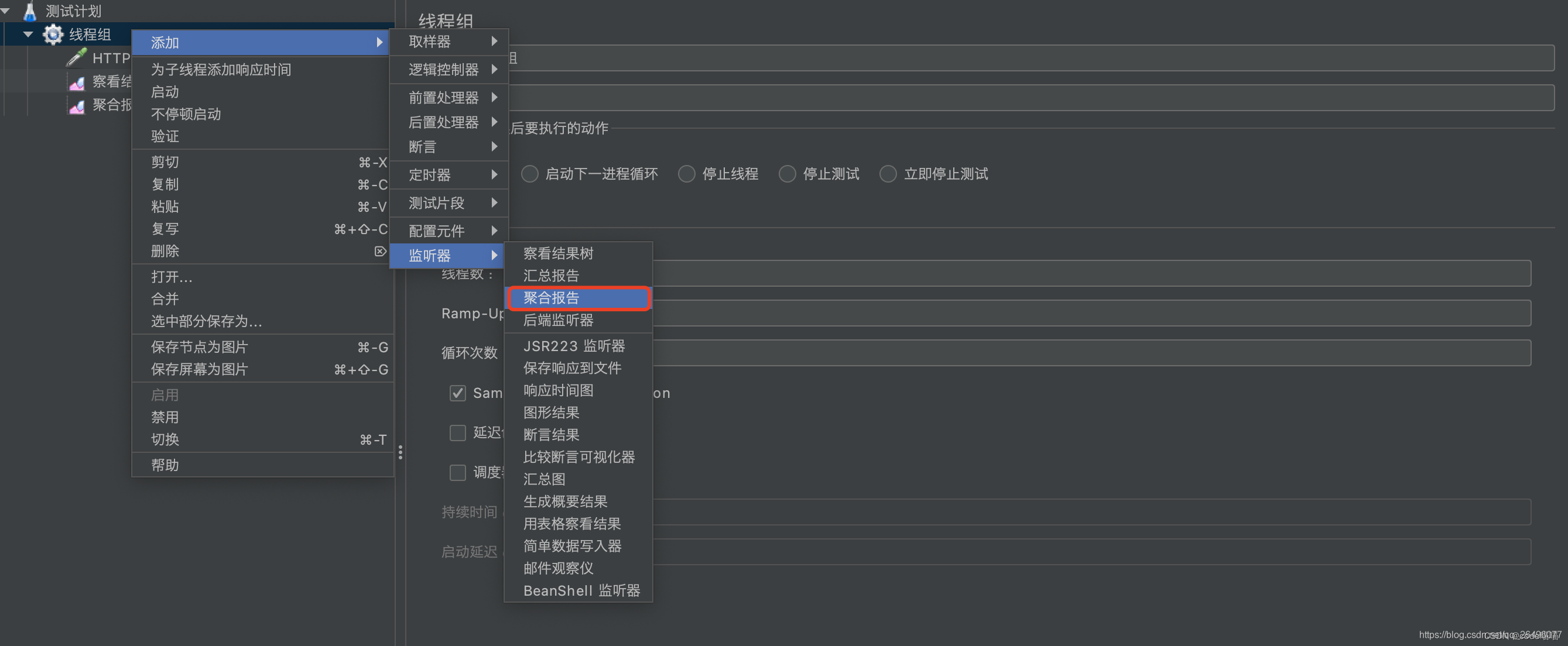
创建聚合报告(显示响应时间、吞吐量、异常数等信息)
点击上方的执行按钮即可开始压力测试
结果树显示
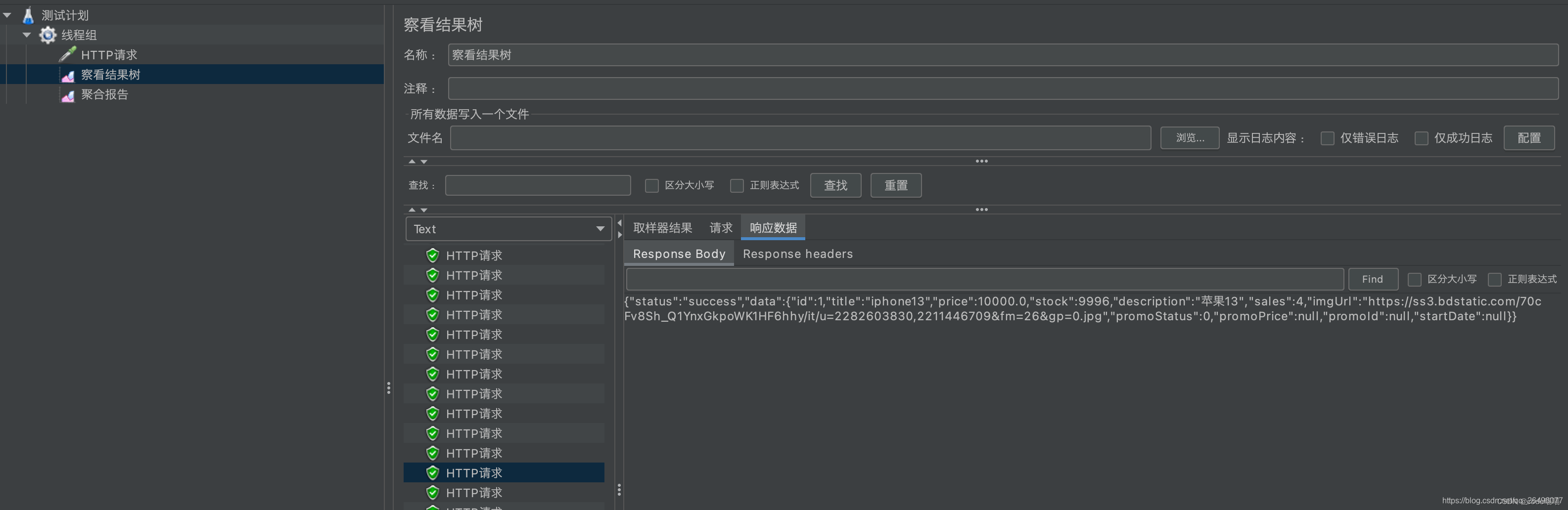
聚合报告结果显示