凡科建设网站靠谱吗国家职业技能培训平台
WEB 3.0 这个名词走进大众视野已经有一段时间了,也曾在各个圈子里火热一时,至今各大互联网企业任旧在 WEB 3.0 上不断探索。但关于 WEB 3.0 是什么这个问题,其实大部分人都没有一个比较明确的认知,包括区块链和元宇宙等相关行业的从业人士在内,也包括我本人亦是如此。本文非技术性文章,从一个普通互联网用户角度,讲讲个人对 WEB 3.0 的理解与看法。
一、什么是WEB 3.0?
在讲 WEB 3.0 前,首先还是需要明确一下,WEB 1.0 和 2.0 的区别。目前我们正处于 WEB 2.0 这个阶段,其实 WEB 2.0 已经能够满足我们目前的绝大部分需求,网上购物、社交乃至于发表文章等等互联网上的操作其实都是非常的方便。这也正是 WEB 2.0 的特性,一系列可交互的互联网平台构建起了 WEB 2.0 的生态。
至于 WEB 1.0,他的侧重点在于数据的展示,定义了 HTML 超链接文本语言,通过一系列的超链接将各个静态页面组合在一起。1.0 是没有交互的,网站上所有的数据来源于网站本身,就好像一张电子化的报纸、公告栏。WEB 2.0 相对于 1.0 的不同主要就体现在于其可交互,这也带动了 AJAX 等网页动态刷新技术的发展。
那什么是WEB 3.0呢?核心要点就是数据的拥有权要回归用户,用户的数据由用户自己进行存储与管理,并通过区块链和密码学技术保证这些信息的隐私性和价值共享。说得简单一点就是数据不再由平台进行存储,所有权在于用户,用户对数据有更强的自主权。
归根结底,所谓 WEB 就是一种数据传输的方式,而 1.0/2.0/3.0 之间的本质区别就是数据存储和传输方式上的区别。各版本数据存储与流向如下图(蓝色节点表示数据存储方):
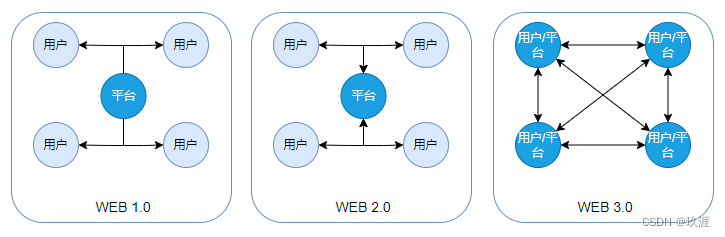
二、WEB的发展
整个互联网,其实就只是一种信息传递的方式。而 WEB 1.0 作为一种信息传输的渠道,解决了信息传递的需求。在 WEB 1.0 时期,各大门户网站纷纷建立,分别发表着自己领域相关的信息(如新闻、产品宣传和文学作品等),各大导航网站再链接着这些大型门户网站,构建出了初代互联网的雏形。
WEB 1.0 解决了信息传递的需求。
随着 WEB 的普及,交互性的需求不断产生,用户不再仅仅渴望浏览信息,也希望发表自己的东西。比如你看见一件感兴趣的商品想要咨询,看到一篇有争议的文章想发表自己的见解,并与其他互联网用户一同讨论。同时用户也不仅局限于浏览网站上的内容,也希望能够通过互联网能够展现自己,与其他用户进行互动。
互联网公司致力于满足用户的这些需求,从中能够获取巨大的商业利益,从技术角度上而言,WEB 2.0 其实也并不复杂,这也是 WEB 1.0 能迅速向 2.0 发展的必然。
交互性的需求促使了 WEB 1.0 向 2.0 发展。
随着 WEB 2.0 这几年来的野蛮发展,相信大家一定会有某些困恼:
- 我注册登录了 N 个网站需要记录 N 个密码,访问不同的网站需要重复登录;
- 我个人发表的文章、著作,网站却拿来收费,并且当做网站的资产,连身为作者的本人都不能随意下载;
- 用户数据发表在互联网之上,其中不乏姓名、年龄等隐私信息,个人隐私安全无法得到保证;
- 身在互联网,却受各个平台掣肘,因为互联网平台的商业利益,用户本身却要受各种限制(比如之前某信上不能发某宝的短连接,比如此处我为何要用“某”?)。
我仅仅列了我目前能想到了几个 WEB 2.0 的弊端,实际上远不止于此,随着互联网的发展,互联网平台、用户和各种数据的数量极具膨胀,用户个性与隐私需求愈发明显。
除了普通用户以外,一些大型央国企、金融机构,他们都有很强的隐私性需求,希望自己能够把握自己的数据,可控的进行数据共享,以发挥数据的最大价值,他们也将是推动向 WEB 3.0 的先锋军。
我粗略的概括的话,那就是用户个性与隐私需求促使了 WEB 2.0 向 3.0 的发展。
而 WEB 3.0 提出的发展方向便是将用户作为主体,保证用户的个性需求和隐私性需求。
三、WEB 3.0 的愿景
WEB 3.0 的愿景是以用户为主导,数据产生于用户,也归属于用户,用户享受这些数据带来的价值。用户在互联网上有统一的身份认证(通行证),通过这个统一身份能够在各个互联网平台上进行认证,并表明用户的数字资产所有权,能够自主的进行数字信息和价值的互联互通,打破互联网平台之间不兼容的限制。
前面我们提到所谓 WEB 就是一种数据传输的方式,从数据层面而言,我们可以定义三个与数据相关的权力:
- 数据所有权: 合法拥有数据的用户/平台,用户/平台对自己创造的数据、付费购买等数据具有所有权;
- 数据存储权: 用户/平台进行数据存储的权力;
- 数据使用权: 用户/平台使用数据的权力,用户/平台可对具有使用权的数据自由的进行分享、出售。
基于 WEB 3.0 的理念,数据的所有权、存储权和使用权这三点都应该归用户所有。而 WEB 3.0 的核心难点也在于如何对数据的权利进行管控,组建一个开放的、平等的、可信的价值互联网,这其中就需要借助于一些密码学技术和数据存证技术。
为了能更轻松理解这一理念,我以一个普通互联网用户的身份来描述一个场景。
我是一个普通的互联网用户,我在一个统一的平台上完成了数字身份认证,这个身份和我的物理身份证完全绑定在一起,听说这个平台底层还使用了区块链技术来保证这个数字身份的安全可信。
我用这个数字身份登录了X音,即兴我拍了一个视频,这个视频在X音上大火,我非常开心,想把这个视频也发布到其他平台上,没想到居然出乎意料的轻松,因为这个视频是由我创作的,我拥有这个视频的所有权,可以将视频发到任何合法的渠道。
有一天,一个不知名的小平台觉得我的视频很有趣,能够吸引很多用户,平台希望将我的视频买下来,我思考了一番,同意了。在一个分布式的区块链平台的见证下,我将这个视频转让给了平台,我没有了这个视频的所有权了,虽然我挺舍不得的,但感觉还是蛮有意思的。
创造价值、分享价值、获得价值,通过 WEB 3.0 让用户完成自我实现。
四、WEB 3.0 的技术
从 WEB 3.0 平台层面来看,区块链与密码学技术是支撑整个平台的基础技术。
讲 WEB 3.0 的建设之前,可以先聊聊云服务器厂商。我们将互联网企业当成一个用户,每个企业自己搭建服务器,自己进行服务器运维,数据完全独立可控,这完全符合 WEB 3.0 的理念。可是除了大型互联网公司和金融相关的企业,绝大多数的中小互联网企业普遍更喜欢云服务作为生产服务器,那为什么会出现这样的情况呢?这些企业不关注数据的隐私吗?我想互联网从业者应该都明白答案,生产服务器要求有很高的稳定性、可靠性和安全性,这其中需要不低的运维成本,中小企业难以维护。
在 WEB 3.0 中,用户具有数据存储权,但是如果真的让用户进行数据存储,让用户提供一台物理设备,还要保证设备的可靠性、安全性等问题,这根本是不可能的事。所以需要一个平台进行数据存储,但无论是任何第三方平台进行数据存储,都不可避免的可能导致平台对用户数据的侵权滥用,所以需要一个去中心化的、分布式的数据存储平台,这个平台需要开放共建,其技术应用在数据、算法和接口等层面上都是公开透明的,用户和各种组织机构能够参与到平台的建设中来,这个平台也就是 DAO (去中心化的自治组织)。从目前而言,最适合做这样的平台的底层技术便是区块链技术。区块链的核心在于分布式存储和分布式账本,在保证用户数据存储与使用流程公开透明的同时也能够进行数据存证,保证数据的可信共享。
但通过区块链还是没办法解决数据的隐私性问题,区块链的核心并不在数据加密,所以还需要其他密码学技术来支撑,保证数据的隐私性。
五、WEB 3.0 的阻力
我想说的是,WEB 3.0 是一个很宏伟的梦,宏伟到根本无法真正实现。
倒不是真正的说 WEB3.0 完全无法实现,仅针对于普通互联网用户,不针对于某些特定行业。在目前阶段而言,WEB 3.0 在普通互联网用户层面的发展会有很大阻力,我归结于以下几点原因。
WEB 3.0 的理念太前卫,影响太广
不同于 WEB 1.0 到 2.0 的迭代,WEB 3.0 整个用户理念都是革命性的改变,用户将在互联网中占主导地位。但是对于大部分互联网用户而言,至今还不清楚 WEB 3.0 为何物,更别说理解 WEB 3.0 的核心理念。
如果要大规模应用 WEB 3.0,那么这些互联网平台需要对接 WEB 3.0 ,这其中涉及到的建设成本就难以估量,所以就算现在政策在大力发展 WEB 3.0 也需要很长的一段过渡时间。这就类似于是 IPv6,始终难以推广。
技术与安全问题难以保证
WEB 3.0 理念是开放共建的,任何组织或个人都有权参与到 WEB 3.0 的建设中来,且相关算法、接口也是开源。开放虽然保证解决了数据存储和使用流程的公开透明,但也让其中的技术缺陷暴露在了大众视野。试想一下,如果有一个非法组织,他没日没夜地钻研平台的技术逻辑,发现了某些漏洞,那么所有的互联网用户数据便都存在安全隐患。
技术难度大。就如区块链而言,个人认为其目前无法作为基础设施支持 WEB 3.0,因为区块链作为一种需要多节点通过共识算法进行共识的程序,其网络需求高、性能还不如一些普通关系型数据库,根本无法支持太大的并发量。现在很多区块链厂商所说的能够支持多少万 TPS,那仅是发起交易的 TPS,如果要等待交易执行完成,那这个数值就要大幅度缩水了。而且参与共识的区块链节点数量越多,共识成本就越大,网络消耗也越高,其性能也就更低了。且区块链节点上的数据都是冗余存储的,这对存储而言也是一大资源消耗。
WEB 3.0 监管方式还有待商榷
对于 WEB 3.0,我想很多人都听说过一个论点:“如今平台掌握着数据,对用户发表的文章、视频有着删除、封禁等大权,而 WEB 3.0 用户具有更高的自主权,就可以避免平台滥用权力。”
我认为这个观点完全是错误的,无论各行各业都离不开各种平台、和政府的监管,否则市场就乱了。普通用户认为平台无端封禁,可如果没有了平台监管,网络上将充斥着各种不良信息、数不清的广告,这么个环境谁又能受得了。
所以,WEB 3.0 确实是以用户为主体,但是权力也终是离不开监管。那么就有一个问题,在 WEB 3.0 这套理念和框架下,如何进行合理有效的监管?如何保证合法用户的合法权益,又能避免非法用户传播不良信息。
损害了部分互联网企业的利益
就目前环境而言,用户的数据都是存储在互联网平台上,平台可自由的对这些数据进行商业分析,通过对这些数据的分析进行商业智能决策。
而如果践行 WEB 3.0 的理念,那么平台所能获得的用户数据将大幅度减少,一些用户画像可能难以进行。虽然目前的隐私计算技术能够解决大部分数据分析统计和智能建模的需求,但这也不可避免的导致企业需要花费更多的成本建设或对接隐私计算平台,甚至可能涉及到还需要向某些数据所有方购买某些数据。
六、我对 WEB 3.0 的看法
WEB 3.0 是一个互联网理念上的大革新,仅能缓慢过渡,可能我有生之年也见不到 WEB 3.0 普及的那一天。
WEB 3.0 的实践仅靠普通的互联网企业难以实现,个人认为 WEB 3.0 中的某些基础设施涉及到用户隐私,需要由国家来牵头建设,就如数字人民币一般。但目前我国对于 WEB 3.0 的政策态度是稳妥推进互联网 WEB 3.0 的发展,整体而言持有的是比较保守的态度。
但 WEB 3.0 的理念在某些行业却能产生很好的商业价值,比如供应链金融领域,这是 WEB 3.0 落地的绝佳场景,供应商、核心企业和各大资金方,这些企业都具有“自主性”,资金方也具有很强的隐私需求,在保证隐私的前提下,又希望进行某些数据共享,从而做一些商业建模和风控分析,这与 WEB 3.0 的思想不谋而合。还有类似金融和一些我不知道的其他行业,他们在 WEB 3.0 上能够获得更大的商业价值,国家政策也在支持他们在 WEB 3.0 上进行探索。
目前整个社会都呈现出一种急功近利,甚至于焦虑的状态,不仅一些互联网巨头在调研 WEB 3.0,很多中小互联网企业都在积极的进行 WEB 3.0 的探索,希望能够把握到这个时代风口,也生怕自己落后于时代而被淘汰。其实就我个人的感受而言,中小企业不必花费太多精力在这上面,企业的技术负责人作为一个技术爱好去了解其实就已经足够了。WEB 3.0 距离我们还很远,就算这些企业探索到了某种 WEB 3.0 的商业模式,也无能去建设。
也有一些企业进行了 WEB 3.0 的尝试,他们运用区块链技术,开发了一系列的元宇宙社交小程序,在平台内充分的应用了区块链技术,能够自由的进行一些数字藏品交易。但是我认为这些平台其实都是“伪 WEB 3.0”,因为他们的藏品交易和用户认证依旧局限在他们平台内部,区块链是他们企业内部的私有链,数据也是存储在他们平台之上。对于他们来说追寻的只是一个商业噱头,用户的自主权并没有真正的得到保证。
综上,我认为目前 WEB 3.0 对于普通互联网用户层面并没有真正的感受到,还是在一个探索阶段,只能说他们促进了 WEB 3.0 相关技术的发展,对于互联网用户理解 WEB 3.0 的生态会有一些帮助吧。也许,这也是一个新技术和思想落地的必然历程,当前不同人对 WEB 3.0 具有不同的定义,以满足自己的价值主张,统一的理念还未形成。
