深圳福田网站建设公司泰安网站建设
前言
嗨喽,大家好呀~这里是爱看美女的茜茜呐

在本篇博客中,我们将讨论 Python 中 for 循环的原理。
我们将从一组基本例子和它的语法开始,还将讨论与 for 循环关联的 else 代码块的用处。
然后我们将介绍迭代对象、迭代器和迭代器协议,还会学习如何创建自己的迭代对象和迭代器。
之后,我们将讨论如何使用迭代对象和迭代器实现 for 循环,以及利用 while 循环通过迭代器协议实现 for 循环逻辑。
最后,我们将反编译一个简单的 for 循环,并逐步介绍 Python 解释器在执行 for 循环时执行的指令,以满足大家的好奇心。
这些有助于理解 for 循环运行时的内部工作原理。
Python的for循环
for 语句是 Python 中执行迭代的两个语句之一,另一个语句是 while。
如果你对 Python 的迭代并不是很熟悉的话,Python中的迭代:for、while、break、以及continue语句是一个不错的切入点。
Python 中,for 循环用于遍历一个迭代对象的所有元素。
循环内的语句段会针对迭代对象的每一个元素项目都执行一次。
暂且可以将迭代对象想象成一个对象集合,我们可以一个个遍历里面的元素。
我们将在下一节对迭代器和迭代对象作详细说明。
👇 👇 👇 更多精彩机密、教程,尽在下方,赶紧点击了解吧~
资料、视频教程、代码、插件安装教程等我都准备好了,直接在文末名片自取就可

一个简单的 for 循环
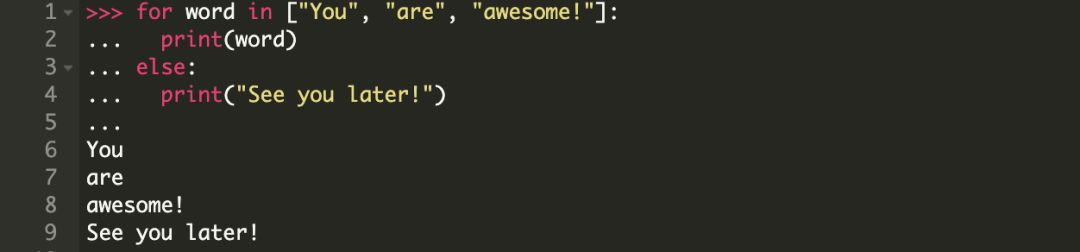
我们先从一个简单 for 循环开始,它遍历一个字符串列表并打印每一个字符串。

如你所见,这个循环实际上遍历了列表中的每一个单词并打印它们。
也就是说,在循环的每一次遍历中,变量 word 都被指定为列表中的一个元素,然后执行 for 语句中的代码块。
由于列表是一个有序的元素序列,所以循环也是以相同的顺序遍历这些元素。
带有 else 子句的 for 循环
Python 中的 for 循环可以选择是否关联一个 else 子句。
else 子句中的代码块是在 for 循环完成后才开始执行的,即在迭代对象中的所有元素都遍历完毕之后。
现在我们看一下如何扩展前面的示例以包含一个 else 条件(子句)。
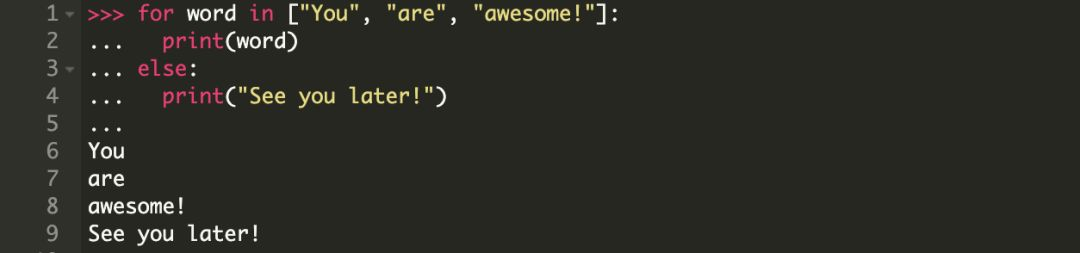
else 子句适用于何时?

你已经注意到,else 子句是在 for 循环完成之后才执行的。
那么 else 代码块的意义是什么呢?for 循环之后的语句不是也是同样会执行吗?
我们很多时候会遇到这样一种情况,当满足某种条件时,中途结束 for 循环。
且如果这个条件一直未满足,则希望执行另一组语句。
我们通常使用布尔类型的标记实现,下面是一个例子:
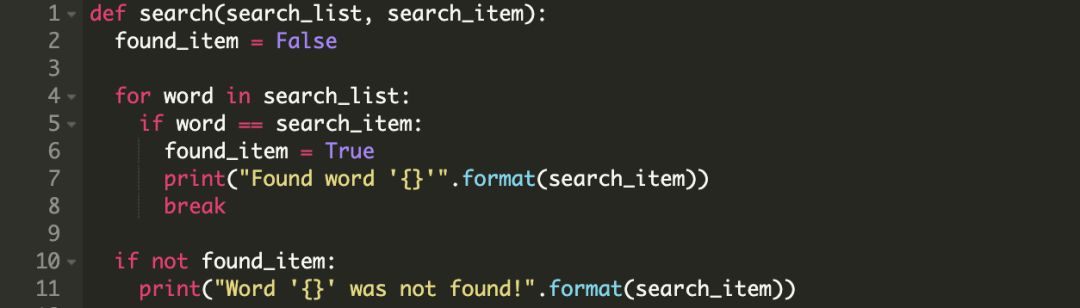
调用结果:

而用 else 代码块的话,我们可以避免使用布尔类型的标记found_item。
我们看看如何使用 else 子句重写上面的方法。
注意:如果 for 循环中的 break 语句被触发执行,那么则会跳过 else 块。

所以 else 代码块适用于 for 循环中有 break 语句的情况,且我们希望 break 条件没有被触发的时候执行一些语句。
否则,与 else 关联的语句只会在 for 循环结束时才执行。
本文的最后一节查看反编译的字节码时你会看到这一点。
for 循环语法
我们已经看到了一些简单的例子,接下来以 for 循环的语法结束本节。

基本上,对于 iterable 中的每一个元素,都会执行 set_of_statements_1。
一旦所有的元素都迭代一遍,控制器将跳转到 else 代码块中执行 set_of_statements_2。
注意,else 子句是可选的。
如果没有发现 else 子句,循环会在所有元素都遍历完成后结束,并且控制器会转向程序之后的语句。
可迭代对象与迭代器
可迭代对象
在上一节,我们使用术语 iterable 来表示循环中被迭代的对象。
现在我们来试着了解一下 Python 中的 iterable 对象是什么。
Python 中,一个 iterable 对象指在 for 循环中可以被迭代的任意对象。
这意味着,当这个对象作为参数传递给 iter()方法时应该返回一个迭代器。
我们来看一下 Python 中的一些常用的内置迭代的例子:
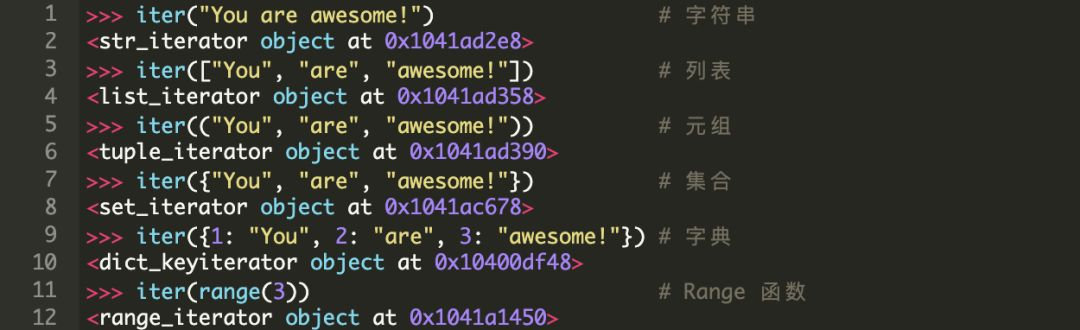
如你所见,当我们对一个 iterable 对象调用 iter() 时,它会返回一个迭代器对象。
迭代器
那么什么是迭代器呢?
迭代器在 Python 中被定义为一个表现为流式数据的对象。
基本上,如果我们将对象传递给内置的next() 方法,它应该从与之关联的流式数据中返回下一个值。一旦所有的元素都遍历结束,它会抛出一个StopIteration 异常。
next()方法的后续调用也都会抛出StopIteration 异常。
我们用一个列表来试一下。
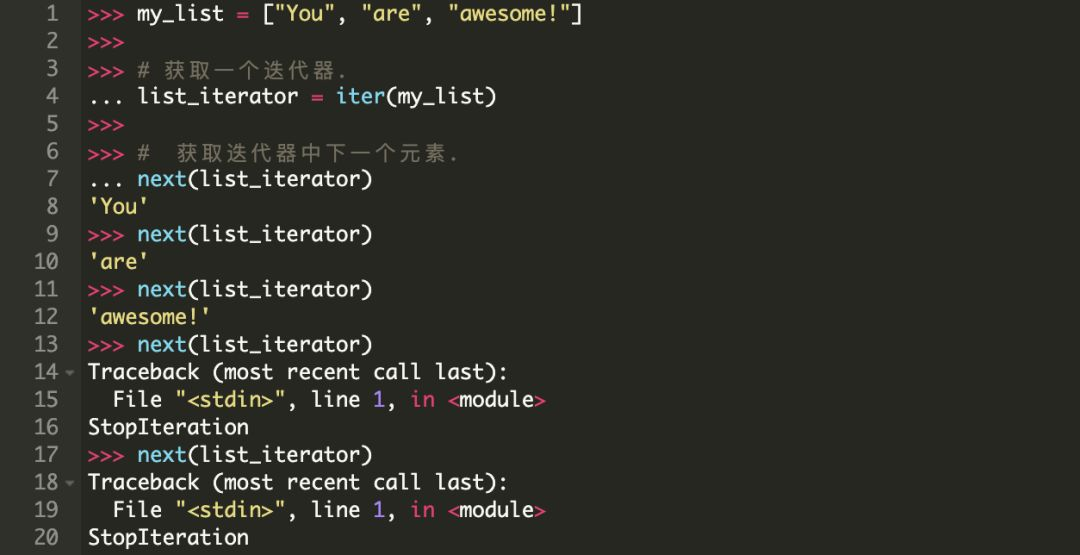
迭代器也是可迭代对象!但是…
有一个很有趣的事需要记一下,迭代器同样支持(强制要求支持迭代器协议)iter() 方法。
这意味着我们可以对一个迭代器调用iter() 方法并获取它自身的迭代器对象。

因此,我们可以在任何期望使用迭代器的地方使用它。
比如,for 循环。
然而要注意一点,在像 list 这样的容器对象上调用 iter() 每次都会返回不同的迭代器,而在迭代器上调用 iter() 仅仅返回同一个迭代器。

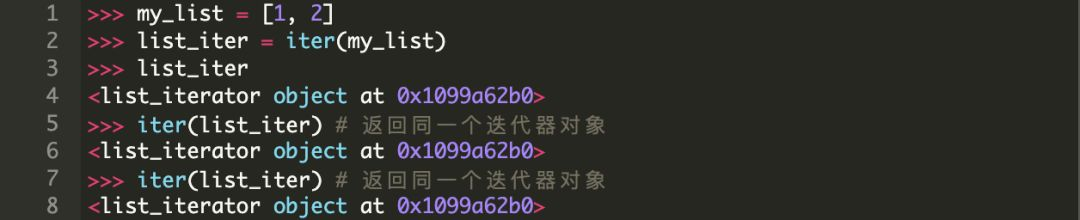
所以如果你需要进行多次迭代,并且用迭代器替换普通容器或可迭代对象,那么第二次你会看到一个空的容器。
对一个列表迭代两次
请注意,这是按照我们的期望运行的。
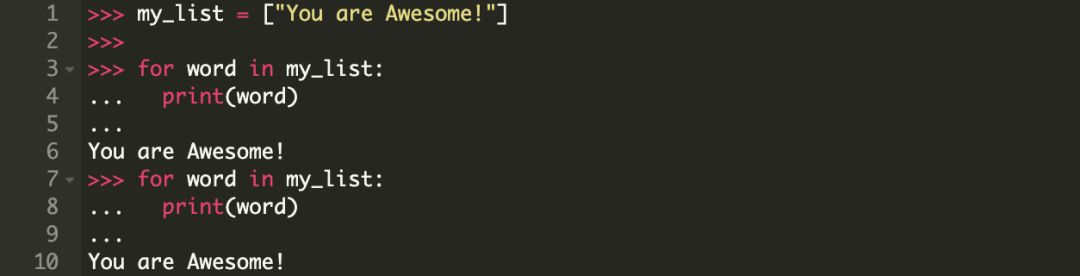
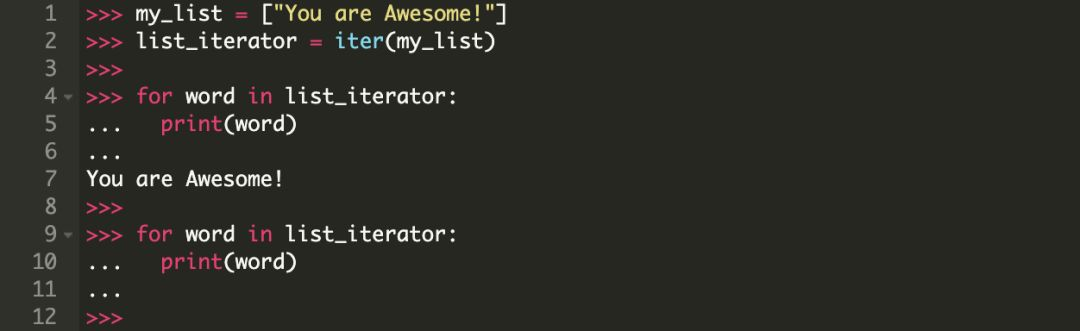
对一个列表迭代器迭代两次
请注意,迭代器在第一次循环的时候就已经结束了,第二次我们看到的是一个空容器。
迭代器协议
前文我们看到了:
-
一个可迭代对象,作为参数传递给 iter() 方法时返回一个迭代器。
-
一个迭代器,
-
作为参数传递给next()方法时返回它的下一个元素或者在所有元素都遍历结束时抛 出StopIteration 异常。
-
作为参数传递给iter() 方法时返回它自身。
-
迭代协议仅仅只是一种将对象定义为迭代器的标准方式。
我们已经在前一节看到了这种协议的实际应用。
根据协议,迭代器应该定义以下两个方法:
-
next()
-
每次调用这个方法时,应该返回迭代器的下一个元素。一旦元素都遍历结束,它应该抛出StopIteration 异常。
-
当我们调动内置函数next() 时,实际内部调用的是本方法。
-
-
iter()
-
这个方法返回迭代器自身
-
当我们调动内置函数iter() 时,实际内部调用的是本方法。
-
自己写一个迭代器
现在我们已经知道迭代协议的原理,可以写一个自己的迭代器了。
我们先看一个例子,下面我们创建了一个根据给定范围和步长的 Range 类。
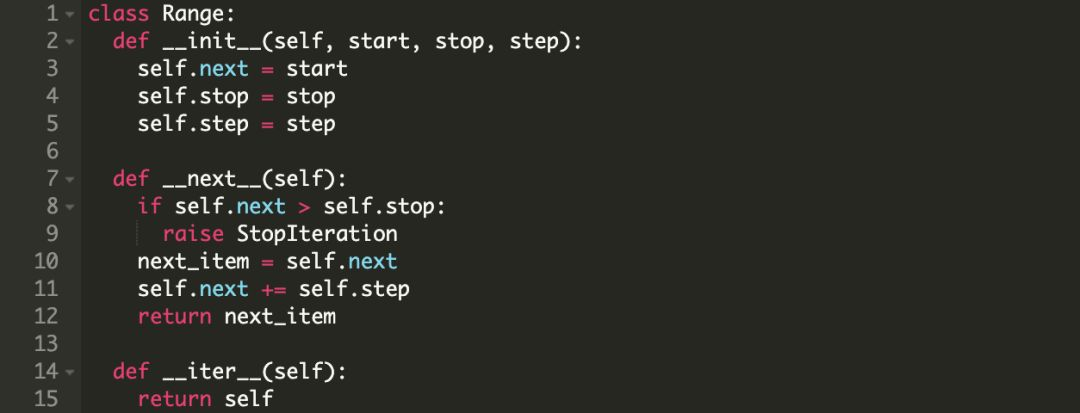
我们看一下它在 for 循环中是怎么工作的。

注意:Range 类的实例是迭代器也是可迭代对象。
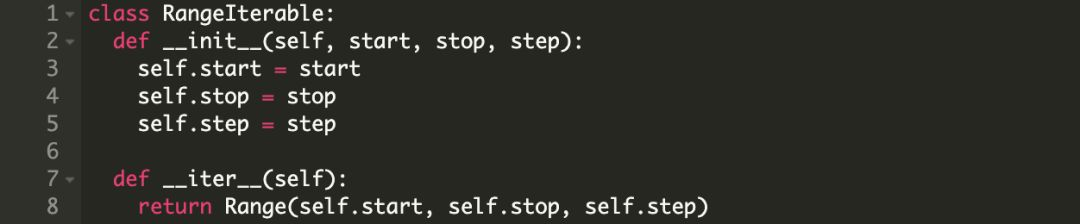
自己写一个可迭代对象
我们还可以基于 Range 迭代器另外创建一个可迭代对象。
它的作用是每当调用 iter() 方法是返回一个新的迭代器,在这里,它应该返回一个新的 Range 对象。
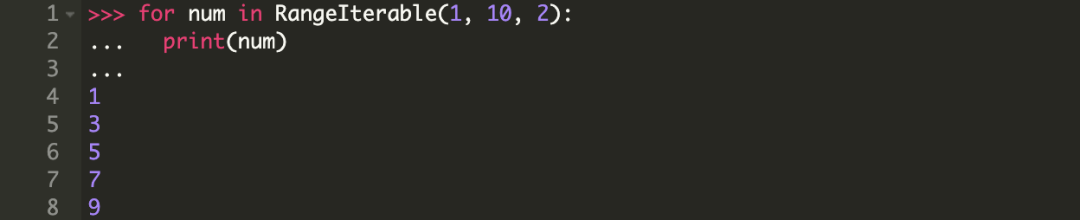
在 for 循环中使用我们这个 RangeIterable。
for 循环工作原理
现在我们已经知道什么是迭代器和可迭代对象,接下来了解一下 for 循环是如何工作的。
再看一下前面的例子。
当我们执行上面的代码块时,发生了以下这些事情:
-
在 for 语句内部对列表 [“You”, “are”, “awesome!”] 调用了 iter() 方法,返回结果是一个迭代器。
-
然后对迭代器调用 next() 方法,并将其返回值赋给变量 word。
-
之后,会执行 for 循环中关联的语句块。这个例子中是打印 word。
-
在 next() 方法抛出 StopIteration 之前会一直重复执行第 2,3 步。
-
一旦 next() 抛出 StopIteration,控制器会跳转到 else 子句(如果存在)并执行与 else 关联的语句块。
注意:如果在步骤 3 中,for 循环语句遇到了 break 语句,则跳过 else 代码块。
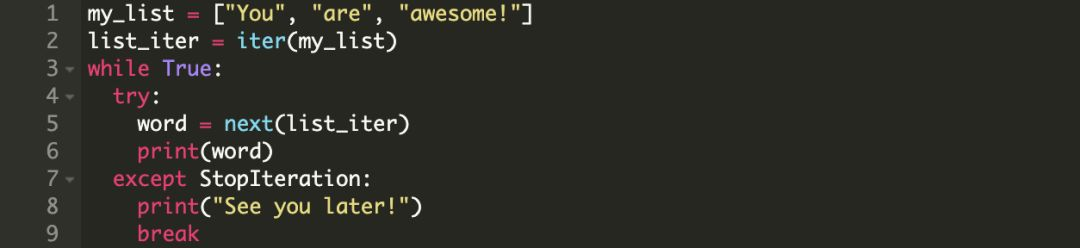
使用 while 语句实现 for 循环逻辑
我们可以像下面这样使用 while 语句实现之前的逻辑。
while 循环的行为实际上与 for 循环相同,上面的代码会有以下输出。

反编译 for 循环
在本节,我们将反编译 for 循环并逐步说明解释器在执行 for 循环时的指令。
这里使用dis 模块来反编译 for 循环。
详细来说,就是我们将使用 dis.dis 方法来生成可读性更高的字节码。
我们会使用之前一直用的简单 for 循环示例。
接下来将文件写入文件 for_loop.py。

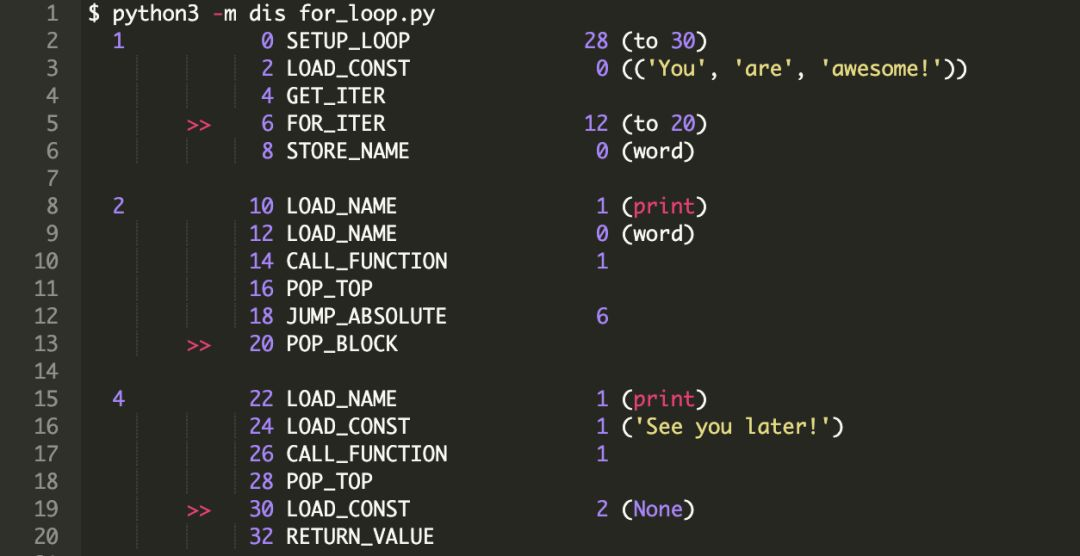
我们可以调用 dis.dis 方法获得可读性高的字节码。在终端上运行以下命令。
更多Python视频、资料、代码加群:926207505免费获取
反编译输出的每列表示以下内容:
-
第 1 列:代码行数。
-
第 2 列:如果是跳转指令,则有 “>>” 符号。
-
第 3 列:以字节为单位的字节码偏移量。
-
第 4 列:字节码指令本身。
-
第 5 列:展示指令的参数。如果括号中有内容,它只是对参数做了更好的可读性转化。
现在我们来一步步浏览反编译后的字节码,并尝试了解实际发生了什么。
第 1 行,即,“for word in [“You”, “are”, “awesome!”]:” 转译为:
0 SETUP_LOOP 28 (to 30)
该语句将 for 循环中的代码块推送到栈中。这段代码块会跨越 28 个字节,达到 “30”。
这意味着,如果 for 循环中有 break 语句,那么控制器将跳转到偏移位置 “30”。
注意当遇到 break 语句时是如何跳过 else 代码块的。
2 LOAD_CONST 0 ((‘You’, ‘are’, ‘awesome!’))
接下来,列表被推送到栈顶(TOS,之后使用 TOS 表示栈顶或栈顶元素)。
4 GET_ITER
该指令实现 “TOS = iter(TOS)”。这表示从列表获取一个迭代器(当前为 TOS),然后将迭代器推送给 TOS。
6 FOR_ITER 12 (to 20)
该指令获取 TOS,作为当前的迭代器, 并调用 next() 方法。
如果 next() 方法产生一个值,则将其作为 TOS 推送到栈,并执行吓一跳指令 “8 STORE_NAME”。
一旦 next() 表明迭代器已经遍历结束(即抛出 StopIteration 异常),TOS(迭代器)将从栈中弹出,字节码计数器会增加 12。这表示控制器跳转到指令 “20 POP_BLOCK”。
8 STORE_NAME 0 (word)
这个指令执行了转换 word = TOS,即,next()返回的值被赋给变量word。
2. 第 1 行,即,“print(word)” 转译为:
10 LOAD_NAME 1 (print)
将可调用方法print 推送到栈中。
12 LOAD_NAME 0 (word)
将栈中的word作为参数推送给print。
14 CALL_FUNCTION 1
调用带位置参数的函数。
像我们看到的指令那样,与函数关联的参数会出现在 TOS 中。在获得可调用象的对(如print)之前,会弹出所有遇到的参数。
一旦获得可调用对象,则把所有参数传递给它并调用。
可调用对象执行结束后,把返回值推送到 TOS 中,这里是 None。
16 POP_TOP
TOS(栈顶元素),即将函数的返回值从栈中移除(弹出)。
18 JUMP_ABSOLUTE 6
此时字节码计数器为 “6”,这表示下一条指令将执行 “6 FOR_ITER”。这是循环遍历迭代器中元素的方式。
注意,一旦迭代器中的元素都遍历结束,指令 “6 FOR_ITER” 会结束循环并跳转到 “20 POP_BLOCK”。
20 POP_BLOCK
POP_BLOCK 会从代码块的栈中移除由 “0 SETUP_LOOP” 设置的代码块。
3. 注意第 3 行(对应else),没有关联任何特殊指令。程序控制器会顺序执行下一条与else 相关的指令。
4. 第 4 行,即,“print(“See you later!”)” 转译为:
22 LOAD_NAME 1 (print)
推送与print 相关的可调用方法到栈中。
24 LOAD_CONST 1 (‘See you later!’)
推送可调用函数的参数对象到栈中。
26 CALL_FUNCTION 1
可调用函数及其参数会从栈中弹出,然后执行函数并将其返回值推送到 TOS。
28 POP_TOP
TOS(栈顶元素),即将函数返回值(这里是 None)从栈中移除。
5. 下面的两个指令只是简单的将脚本的返回值(None)加载到栈并返回。
30 LOAD_CONST 2 (None)
32 RETURN_VALUE
喔!现在我们已经了解了 for 循环反编译后的指令。
希望这有助于更好地理解 for 循环的工作原理。
尾语
感谢你观看我的文章呐~本次航班到这里就结束啦 🛬
希望本篇文章有对你带来帮助 🎉,有学习到一点知识~
躲起来的星星🍥也在努力发光,你也要努力加油(让我们一起努力叭)。

