网站服务器做哪些安全措施网站百度不收录的原因
apscheduler使用比较简单,每隔一段时间自动化运行的步骤是:
- 创建调度器
scheduler = BlockingScheduler() - 添加任务
scheduler.add_job(函数名, 'interval', minutes=30) # 每隔30分钟运行一次 - 直接执行:
scheduler.start()
示例代码
from datetime import datetime
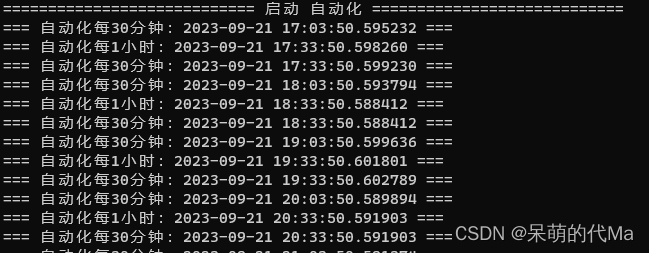
from apscheduler.schedulers.background import BlockingSchedulerdef print_30_second():"""自动化:每30分钟"""print(f"=== 自动化每30分钟:{datetime.now()} ===")def print_each_hour():"""自动化:每1小时"""print(f"=== 自动化每1小时:{datetime.now()} ===")def main():print("============================ 启动 自动化 ============================")# 1.创建调度器scheduler = BlockingScheduler()# 2. 添加任务scheduler.add_job(print_30_second, 'interval', minutes=30)scheduler.add_job(print_each_hour, 'interval', hours=1)# 3.满足条件执行器scheduler.start()if __name__ == '__main__':main()
效果图