邢台太行中学最新seo自动优化软件
本文整理自百度云智峰会 2024 —— 云原生论坛的同名演讲。

今天给大家介绍下百度沧海·存储团队在数据湖加速方面的工作进展情况。
数据湖这个概念,从 2012 年产生到现在已经有十余年的时间,每家公司对它内涵的解读都不太一样。但是数据湖的主要存储底座有从传统的 HDFS 向对象存储演进的趋势。
传统的大数据计算场景,比如 MapReduce、Spark、Hive 这些大数据组件都是基于 HDFS 构建的。但是,它有如下几点不足:
-
第一个是资源问题。由于 HDFS 计算资源和存储资源混布在一起,只有计算和存储资源匹配,才不会出现资源的浪费。这对业务发展趋势的规划能力要求是非常高的,实际业务中很难预测 3 年、5 年之后的计算和存储的规模变化,如果出现不匹配,会出现某种资源的浪费。
-
第二个是规模问题,单个 HDFS 集群的 Namenode 最高支持 10 亿量级的规模的文件数,现在大模型训练文件数最高会超过百亿,甚至千亿的文件规模, HDFS 集群很难满足,虽然有一些改进方案,如集群的 Federation 可以使支持的规模变得大一些,实际上会牺牲很多特性,带来使用上的不便。
-
第三个运维问题。HDFS 运维负担比较重,需要有丰富的 HDFS 运维经验的工程师才能解决数百 PB 规模集群的可靠性、可用性问题。
对象存储的出现可以很好的解决 HDFS 存在的问题:
-
对象存储作为存储组件是存算分离的架构,计算和存储可以独立扩容,具有更大的弹性。
-
对象存储扩展性要好,支持的规模更大,并具有云原生的无运维负担、多级存储体系成本低等特点。

对象存储作为数据湖存储底座能完美的代替 HDFS 吗?
这里还是有诸多挑战需要解决:
第一个挑战是性能问题。存算分离有弹性的优势,但是性能有下降。在元数据维度,HDFS Client 访问 HDFS Namenode,一次元数据操作只需要几百微秒。而对象存储要经过鉴权、协议转换再加上由于计算节点和存储节点延迟变高的原因,延迟会有增加。在数据面维度,由于要经过网关节点、对象存储前端、以及对象存储后端,相比于 HDFS,数据吞吐会有很大的衰减。
第二个挑战是 HDFS 上游计算生态的兼容性问题。上游的大数据组件 MR、Spark、Hive 这些都是基于 HDFS 构建的,对象存储在访问协议、鉴权方式存在非常大的差异。如何屏蔽这些差异,对上游业务无感实现平滑切换,这也是一个非常棘手的问题。

为了更好的加速上层大数据、AI 计算业务,发挥存储底座的基础支撑作用,百度沧海在数据湖存储加速方案 1.0 的基础上,发布了数据湖存储加速 2.0 版本,在新版本中:
-
升级了层级 Namespace 2.0 版本,实现了基于规模的自适应存储架构,达到了规模和性能的有效平衡。
-
在对象存储后端升级了对大数据更加友好的流式存储引擎。相比于 HDFS,单流吞吐提升 70% 以上。
-
在计算侧缓存我们发布了 RapidFS 托管型产品,能够更高效的实现数据缓存和写入加速。
-
同时,发布了 BOS-HDFS 全新版本,实现了对 HDFS API 100% 兼容,能够实现上层业务无缝对接和迁移。
下面分别展开介绍一下各个方面的内容。

先看一下 Namespace 的演进路线。
对象存储有两套 Namespace 体系,一个是平坦 Namespace,另外一个是层级 Namespace。平坦 Namespace 对大数据计算来说有 rename 原子性和性能问题,省去不谈,这里重点讲一下层级 Namespace 的演进。
-
第一代的层级 Namespace 方案,是单机的方案,最典型的代表是 HDFS 的目录树全内存方案,这种方案性能高,但是扩展性差,只能在 10 亿的量级。有的系统把目录树全内存扩展到了 SSD,部分热数据放内存或者一些系统做了静态子树划分的扩展方案,支持的规模有一定的增加,但是扩展的不多。
-
第二代的层级 Namespace 基于分布式数据库构建,典型的代表是 Facebook 的 Tectonic 系统,优点是线性扩展,支持的规模大,缺点在创建文件、rename 时候会触发多次 RPC 和两阶段提交,延迟相当于单机方案会比较高。
-
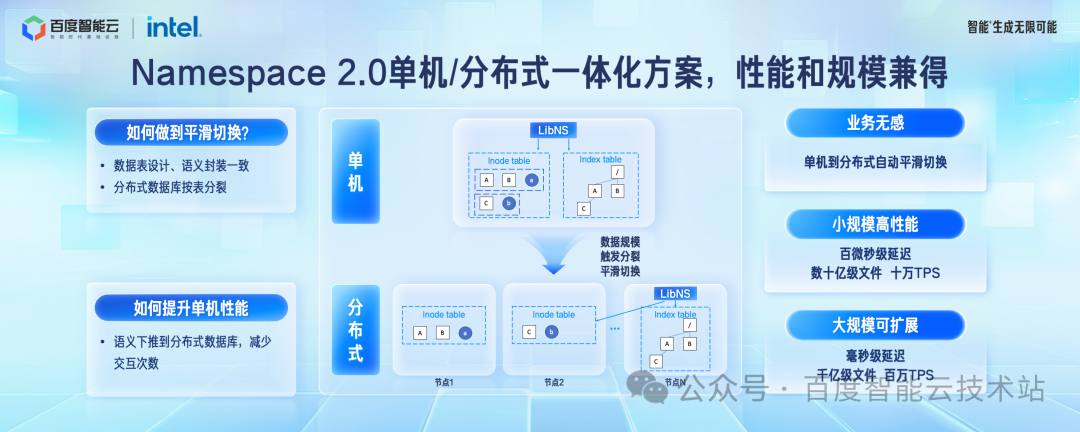
百度提出的第三代层级 Namespace 系统是「单机/分布式一体化方案」,能够做到规模自适应。在规模小的时候具备单机 Namespace 系统的性能优势,百微秒级延迟。在规模扩大到必须采用分布式方案的时候,能够无感平滑迁移到分布式架构,满足规模的水平扩展,适应各个阶段的要求。

单机和分布式架构能够做到合二为一的最核心的一个点是在规模达到临界点的时候,后端架构如何做到平滑切换。
我们是这样做的,无论是单机架构和分布式架构,我们都基于我们自研的分布式数据库去构建,也就是百度沧海的元数据底座 TafDB。
在单机架构下,我们强制层级Namespace依赖的Inode信息和目录树信息绑定分配到同一组存储节点。这个时候,不需要跨机事务和多次 RPC 就可以完成文件创建、目录 rename 等元数据操作,这时候跟单机架构的延迟一致。
当桶的文件规模达到 10 亿量级的临界点之后,会触发分布式数据库按不同的表边界分裂。分布式数据库的分裂操作对上层业务无感,Inode 表动态水平扩展,这个时候单机事务转换为跨节点事务,单次 RPC 转换为多次 RPC,上层 Lib 库对这两种接口进行了很好的的封装,上层 API 一致。
这样单机架构就可以平滑的过渡到分布式架了,分布式架构的性能相对于单机架构有一些衰减,单次操作到毫秒级延迟,但是规模可以支撑到百亿到千亿的规模。
在单机架构下还有一个问题待解决,就是如何提升系统的吞吐。我们的做法是把文件语义操作下推到分布式数据库层,直接使用数据库的内置语义完成操作,减少跟上层组件的通讯次数,单桶支持到十万 TPS。
在对象存储后端数据面的引擎优化方面,我们针对大数据和 AI 场景进行了优化升级。
原来的存储引擎专门针对小文件设计,数据按 Blob 切块之后,数据块随机放到整个集群的磁盘上,这样可以充分分散压力,利用数十万块磁盘的 I/O 能力。
大数据计算有文件大、顺序读的特点。针对这个特点,我们升级了存储引擎,整个文件切成更大的 Block,Block 内部顺序放置。
这样既不会出现热点,又可以充分发挥 HDD 顺序访问高吞吐的优势,一次性预读更多的数据,单流吞吐可以达到 300MB/s,相比于原生 HDFS 单流的带宽提升 70% 以上。

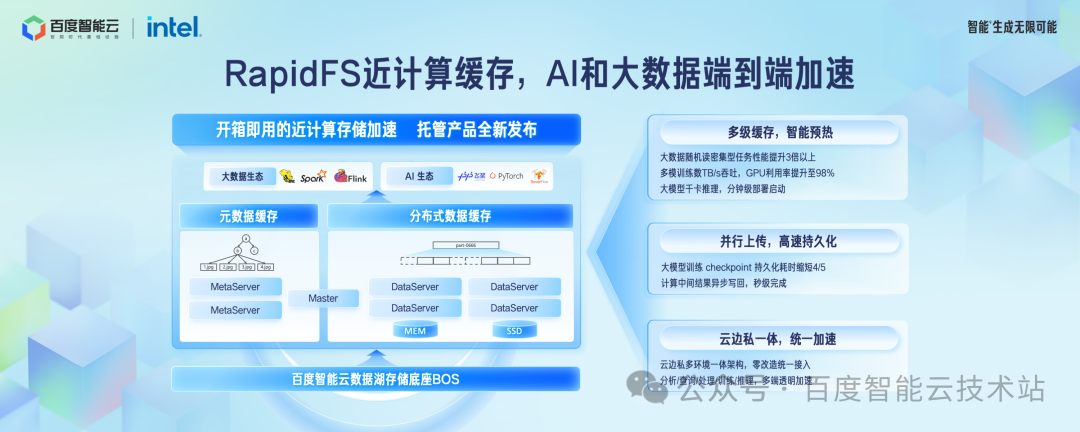
在近计算侧的缓存加速方面,我们发布了 RapidFS 托管型产品,端到端加速大数据和 AI 应用。
对于随机读密集型的计算场景,I/O size 很小,对象存储性能较差,这时候把大块数据缓存到 RapidFS,可以更好的发挥出优势,性能提升 3 倍以上。
在多模态训练场景,通过智能预热到 RapidFS 做训练加速,使得 GPU 使用率提升 98% 以上。
在推理集群模型文件分发场景,RapidFS 支持复制出更多的副本数来分摊读压力,使得千卡推理集群的模型部署在分钟级完成。
对于大模型训练 Checkpoint 持久化场景,数据先写入 RapidFS 的分布式缓存,再异步写到后端的对象存储集群,Checkpoint 持久化耗时缩短了 4/5。
数据湖存储加速 RapidFS 在专属云、边缘云、公有云都提供了一体化的架构,业务可以实现零改造成本统一接入。
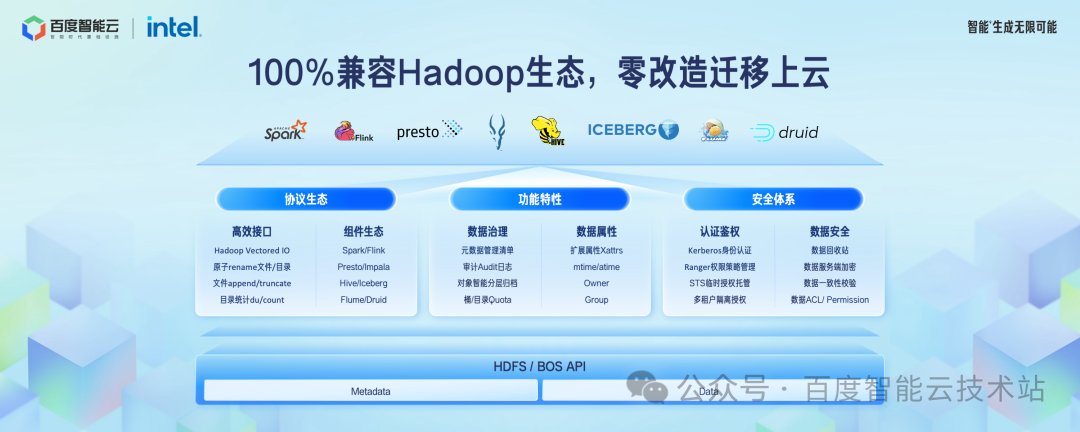
在 Hadoop 生态兼容方面,我们发布了 BOS-HDFS 全新版本,对上层 Hadoop 应用提供 100% 的兼容,无需修改代码就可以运行原有的大数据和 AI 任务,实现零改造迁移上云。
BOS-HDFS 提供了原子 rename、Vectored I/O、文件 append/truncate 等 Posix 文件语义接口。
BOS-HDFS 兼容所有主流计算引擎,并且在这个基础上,提供了额外的智能数据分层、子目录 Quota、日志审计、服务端加密等更丰富的功能。
在认证鉴权方面提供了 Kerboeros + Ranger 到临时 token 鉴权体系的无缝转换方案。
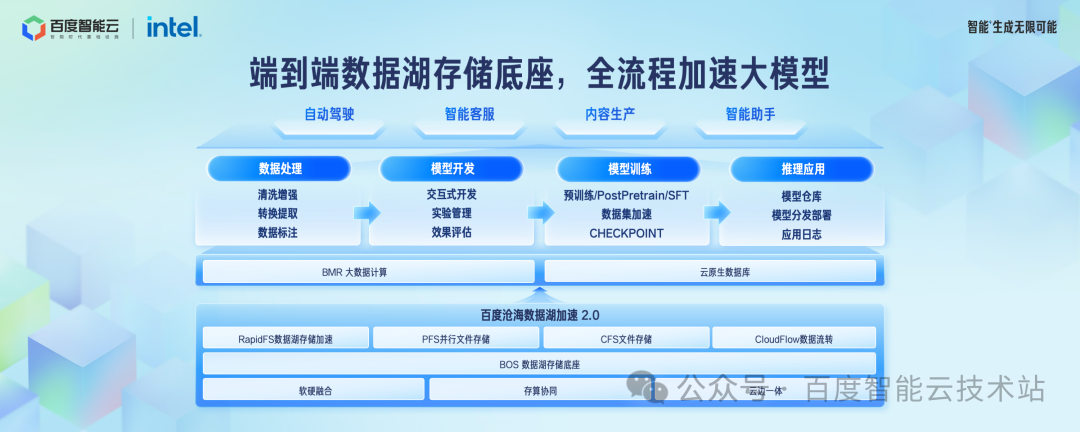
这张图是百度沧海支持大模型场景的全景图。
对象存储 BOS 作为基础的数据存储底座,数据湖存储加速 RapidFS、文件存储 CFS、并行文件存储 PFS 作为加速层,在数据处理、模型开发、模型训练、模型推理各个环节,我们都提供了完善的端到端解决方案。
下面介绍下典型应用案例。
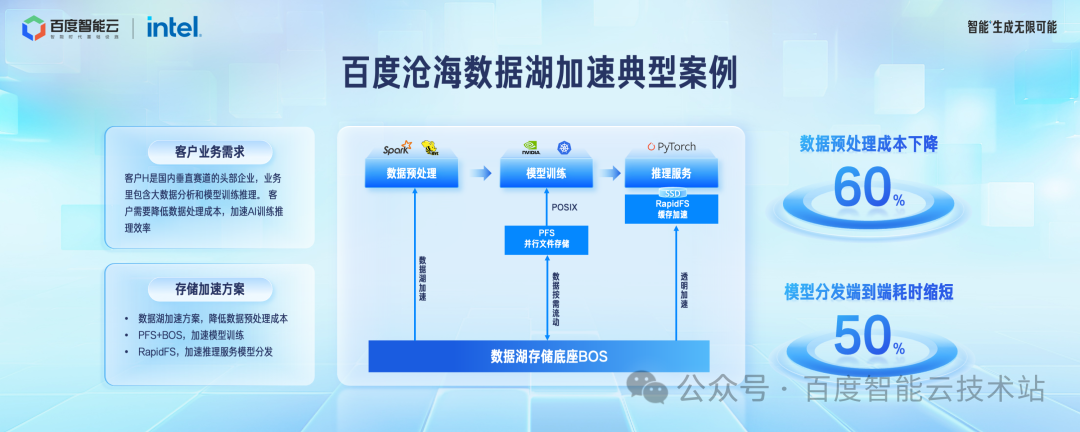
客户 H 是国内垂直赛道的头部客户,在百度智能云上构建自己的 AI 应用。
-
在数据预处理阶段,使用对象存储 BOS 作为数据湖存储底座处理待训练的数据,相比于自建的 HDFS 模式,成本下降了60%。
-
在模型训练阶段,使用 PFS + BOS 的加速方案。热数据按需加载到 PFS,冷数据存放到 BOS。
-
在模型推理阶段,使用 RapidFS 做模型分发的加速。相比于之前的方案,模型分发的端到端延迟缩短了 50% 以上。
以上就是这次的全部分享,谢谢大家!
