天水做网站seo公司排名
目录
一、前言
二、元数据简介
1、元数据定义
2、元数据分类
3、数据库元数据管理
三、GaussDB数据库的元数据管理
1、GaussDB数据库的元数据管理
2、通过“SQL + 系统表/系统视图/系统函数”的方式管理(采集)元数据
1)获取表、视图及表字段等信息
2)获取定时任务信息
3)获取索引信息
4)获取存储过程、函数、触发器等信息
四、小结
一、前言
GaussDB是一种分布式的关系型数据库,元数据(表、列、视图、索引、存储过程等对象)是其重要的一部分。元数据是指描述数据的数据,包括数据的定义、结构、属性、关系等信息。本文以GaussDB物理数据库为主,结合元数据的概念简单介绍一下相关内容。
二、元数据简介
1、元数据定义
按照传统的定义,元数据(Metadata)是描述数据的数据。元数据主要记录数据库应用系统中模型的定义、各层级间的映射关系、监控数据库应用系统的数据状态及ETL的任务运行状态等。在数据库应用系统中,元数据可以帮助数据库管理员和开发人员非常方便地找到其所关心的数据,并用于指导其进行数据管理和开发工作,提高工作效率。
2、元数据分类
元数据可根据不同的维度进行分类,按用途的不同,可以分为两类:技术元数据(Technical Metadata)和业务元数据(Business Metadata)。
- 技术元数据是存储关于数据库应用系统技术细节的数据,是用于开发和管理数据库应用系统使用的数据。技术元数据即为技术资产,显示数据库、数据表、数据量的数量及其详情。
- 业务元数据从业务角度描述了数据库应用系统中的数据,它提供了介于使用者和实际系统之间的语义层,使得不懂计算机技术的业务人员也能够“读懂”数据库应用系统中的数据。业务元数据包含业务资产和指标资产,业务资产显示业务对象、逻辑实体、业务属性的数量及其详情,指标资产显示业务指标及其详情。
3、数据库元数据管理
元数据管理是对数据采集、存储、加工和展现等数据全生命周期的描述信息,帮助用户理解数据关系和相关属性。 数据库的元数据指的是关于数据库对象(如表、列、索引、视图、存储过程等)的信息,这些信息描述了这些对象的结构和属性。并且最终目标是服务于数据库应用系统的高效实施(开发、管理、维护等)。
三、GaussDB数据库的元数据管理
1、GaussDB数据库的元数据管理
通过登录GaussDB提供的“数据管理服务(DAS)” 工具,进入“库管理(Schema列表/对象列表/元数据采集)”主页面,可进行相关元数据的基础管理(如下图)。
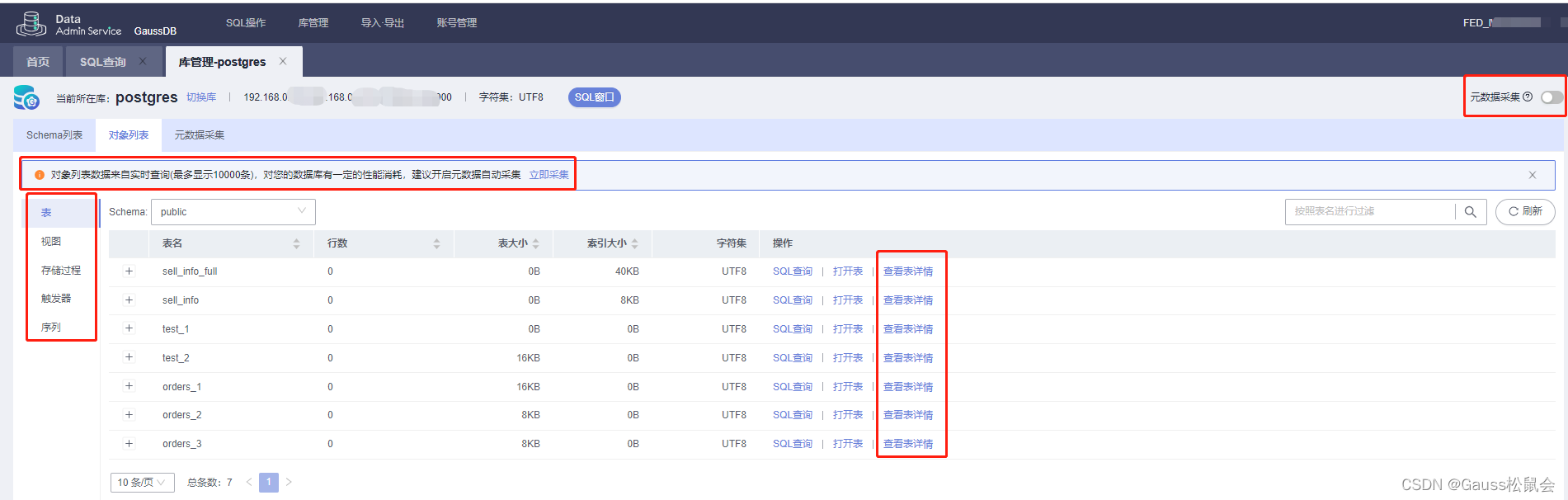
GaussDB数据库对象列表:
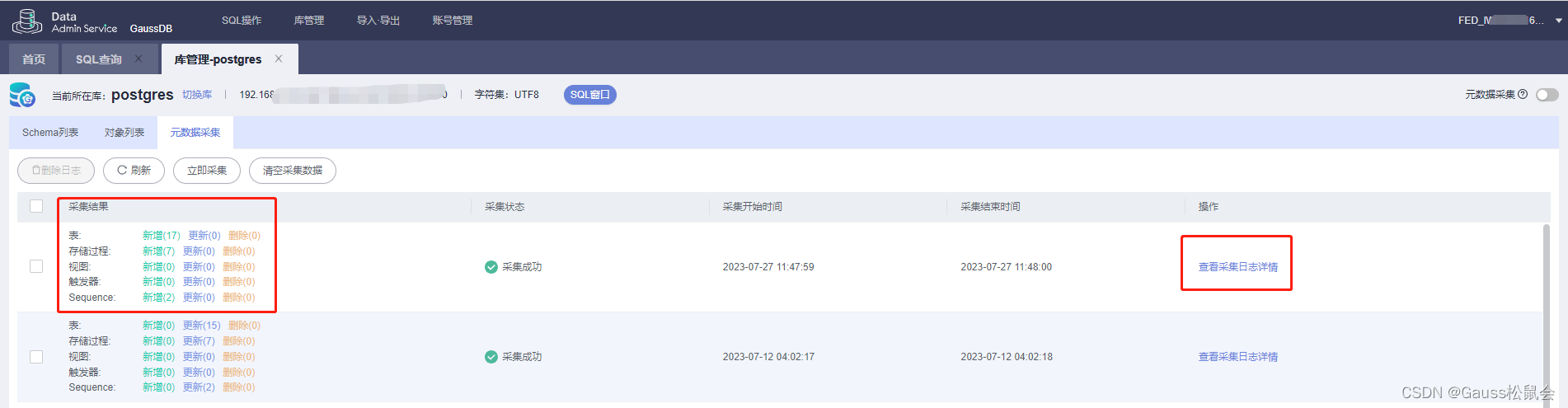
 GaussDB数据库元数据采集(DAS工具内置功能):
GaussDB数据库元数据采集(DAS工具内置功能):
Tip:对象列表数据来自实时查询(最多显示10000条),对数据库有一定的性能消耗,建议开启元数据自动采集。
2、通过“SQL + 系统表/系统视图/系统函数”的方式管理(采集)元数据
1)获取表、视图及表字段等信息
(1)PG_GET_TABLEDEF(tablename)系统信息函数,获取表定义信息。
| SELECT * FROM PG_GET_TABLEDEF(‘test_1’); |
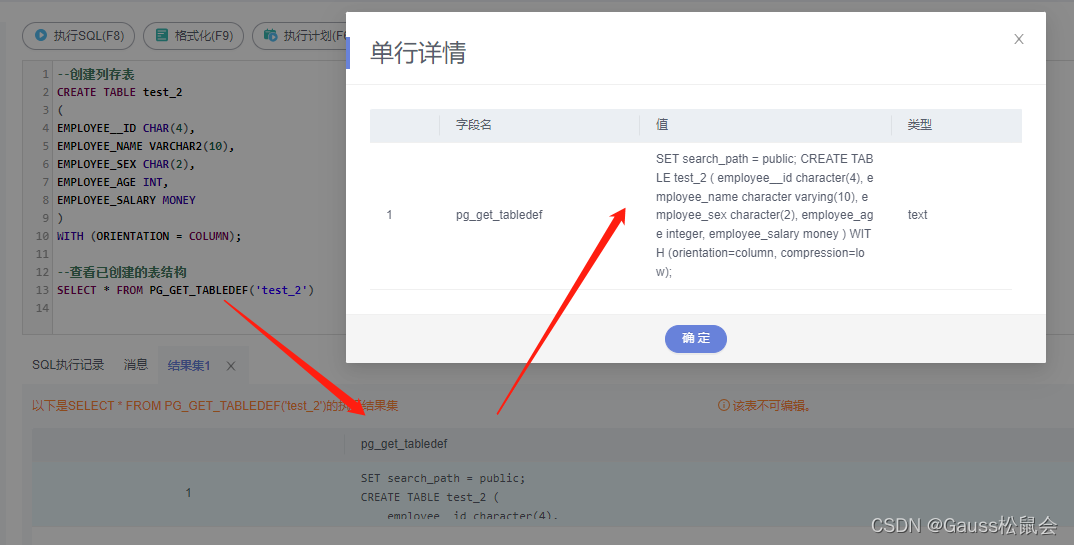
返回类型:text。说明:pg_get_tabledef重构出表定义的CREATE语句,包含了表定义本身、索引信息、comments信息。对于表对象依赖的group、schema、tablespace、server等信息。
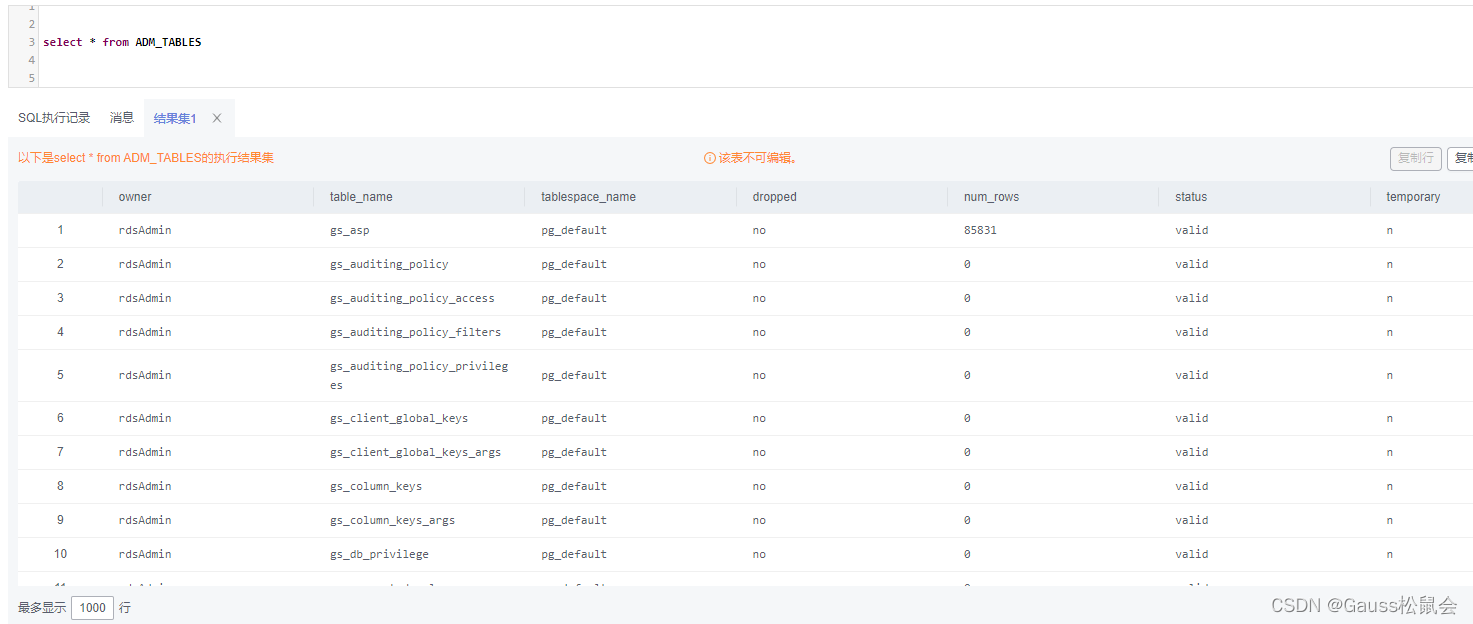
(2)ADM_TABLES视图存储关于数据库下的所有表信息。主要字段:表的所有者、表名、存储表的表空间名、表的估计行数、是否为临时表等
| SELECT * FROM ADM_TABLES; |
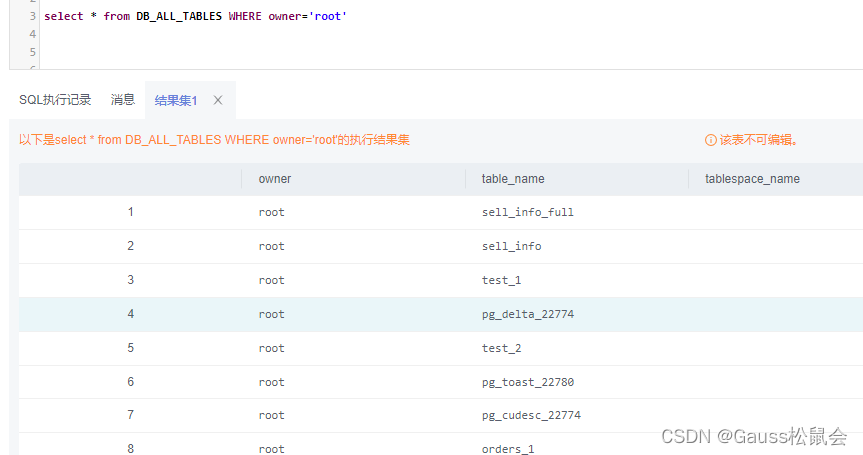
(3)DB_ALL_TABLES视图存储当前用户所能访问的表或视图。主要字段:表或视图的所有者、表或视图的名称、表或视图所在的表空间。
| SELECT * FROM DB_ALL_TABLES; |
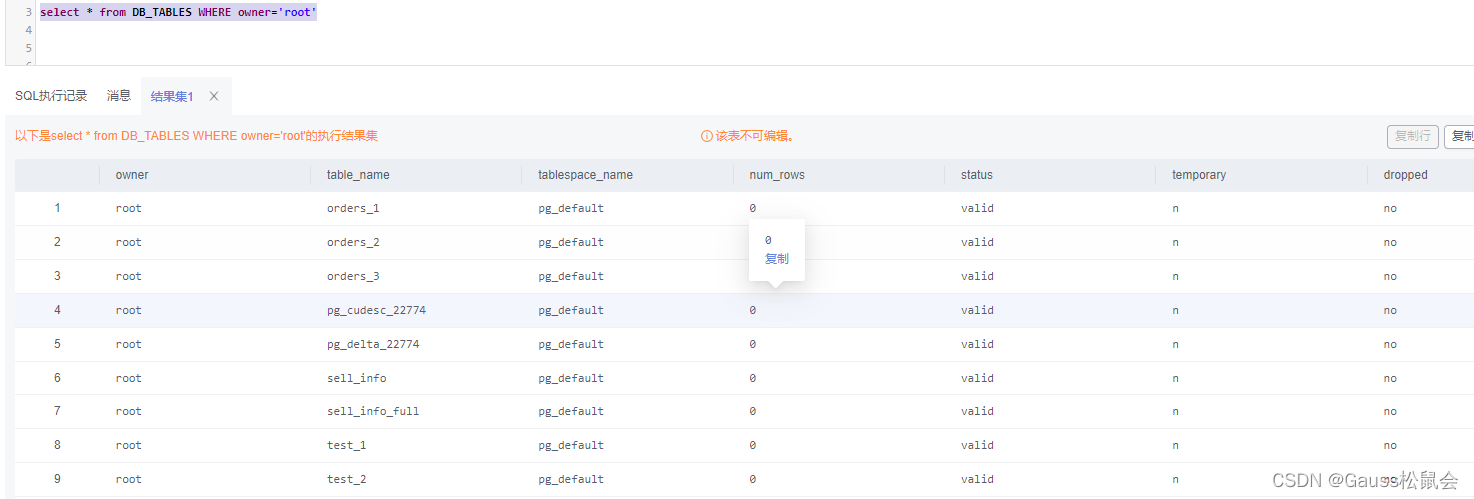
(4)DB_TABLES视图存储当前用户可访问的所有表。主要字段:表的所有者、表名、存储表的表空间名、表的估计行数、是否为临时表等。
| SELECT * FROM DB_TABLES; |
(5)ADM_TAB_COLUMNS视图存储关于表和视图的字段信息。数据库里每个表或视图的每个字段都在ADM_TAB_COLUMNS里有一行。主要字段:表的所有者、表的名称、列名、列的数据类型、列的字节长度等。
| SELECT * FROM ADM_TAB_COLUMNS; |

(6)DB_TAB_COLUMNS视图存储了当前用户可访问的表和视图的列的描述信息。主要字段:表的所有者、表的名称、列名、列的数据类型、列的字节长度等。
| SELECT * FROM DB_TAB_COLUMNS; |

2)获取定时任务信息
MY_JOBS系统视图获取其定义信息。主要字段:作业创建者、作业执行者、作业对应的数据库名称、开始执行时间、结束时间、运行状态等。
| --获取定时任务信息 SELECT * FROM MY_JOBS; |

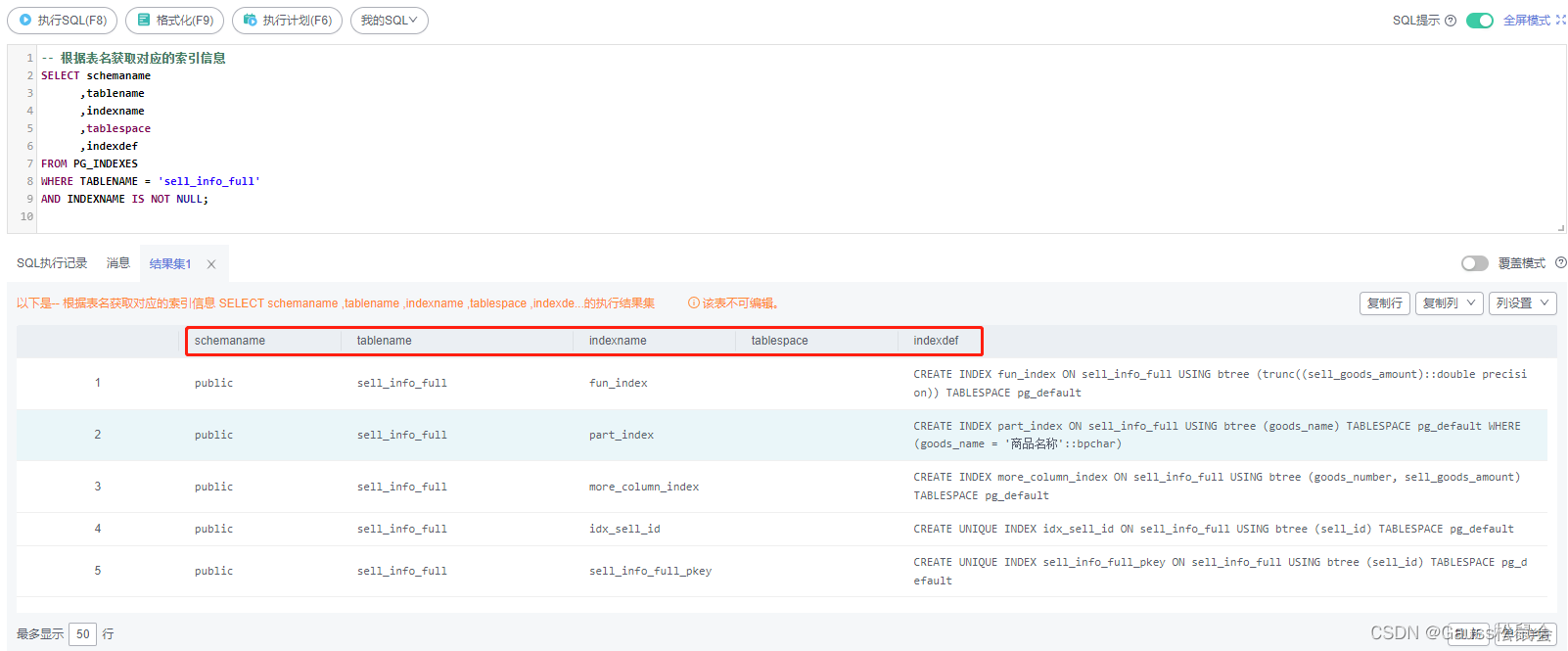
3)获取索引信息
PG_INDEXES系统视图获取表中的索引信息
| -- 根据表名获取对应的索引信息 SELECT schemaname ,tablename ,indexname ,tablespace ,indexdef FROM PG_INDEXES WHERE TABLENAME = 'sell_info_full' AND INDEXNAME IS NOT NULL; |
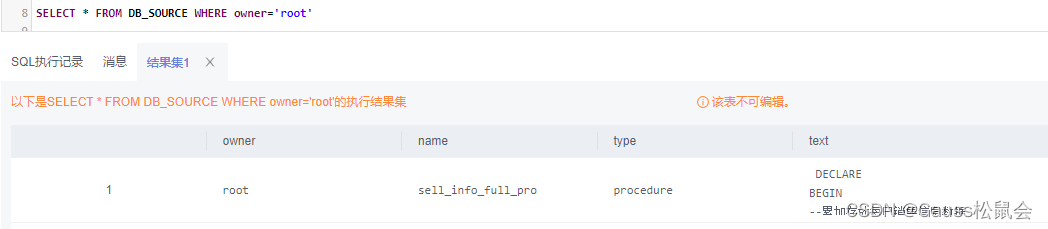
4)获取存储过程、函数、触发器等信息
DB_SOURCE视图存储当前用户可访问的存储过程、函数、触发器的定义信息。该视图同时存在于PG_CATALOG和SYS schema下。 主要字段:对象的所有者、对象名字、对象类型(function, procedure, trigger)、存储对象的文本来源等。
| SELECT * FROM DB_SOURCE; |
GaussDB数据库元数据的获取/采集主要是以系统表、视图、函数等方式获取,其元数据不止包含TABLES、VIEWS、COLUMNS、SOURCE、JOB,还包括USERS、COMMENTS等。 具体可根据实际业务需要进行采集管理。
四、小结
元数据管理从技术角度,元数据管理着企业的数据源系统、数据平台、数据仓库、数据模型、数据库、表、字段以及字段间的数据关系等技术元数据。从业务角度,元数据管理着企业的业务术语表、业务规则、质量规则、安全策略以及表的加工策略、表的生命周期信息等业务元数据。从应用系统角度,元数据管理为数据提供了完整的加工处理全链路跟踪,方便数据的溯源和审计,这对于数据的合规使用越来越重要。通过数据血缘分析,追溯发生数据质量问题和其他错误的根本原因,并对更改后的元数据进行影响分析等。
GaussDB数据库的元数据管理是数据库系统管理工作的核心之一。它可以帮助用户更好地管理和维护数据库,提高数据的安全性和可靠性,减少数据丢失和损坏的风险。同时,元数据管理还可以帮助用户更好地理解和使用数据库,提高工作效率 。
——结束
