孟村建设局网站软文网站
文章目录
- 一、OSI七层参考模型
- 二、TCP/IP体系结构
- 三、TCP/IP参考模型
- 四、沙漏计时器形状的TCP/IP协议族
- 五、两种国际标准对比
- 相似之处
- 不同之处
一、OSI七层参考模型
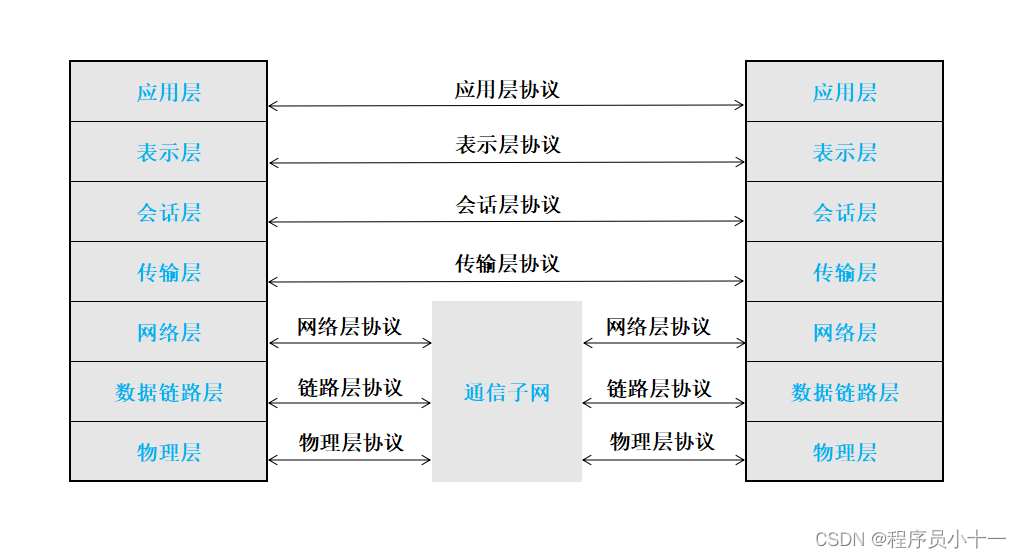
OSI参考模型共分为7层,低三层面向通信,可用软硬件实现;高三层面向信息处理,一般由软件实现;传输层起联系上下层的作用;其中,路由器只有物理层、链路层、网络层三层协议。
二、TCP/IP体系结构
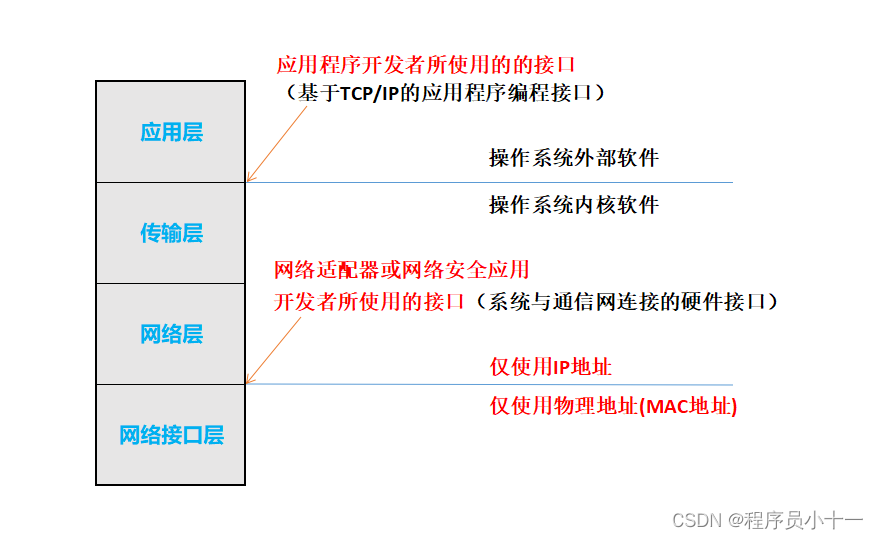
- TCP/IP 是四层的体系结构:应用层、传输层、网络层和网络接口层。
- 网络接口层可以包括多种通信网,如以太网、电话网、PPP、同步数字系列(SDH)等,因特网体系结构仅关注了网络层与这些通信网的接口,如何传输帧是通信网自己的事情。
- IP协议支持多种网络技术互联以形成一个逻辑网络,提供了主机到主机的端到端通道。
- TCP、UDP提供了应用进程的端到端传输通道。
三、TCP/IP参考模型
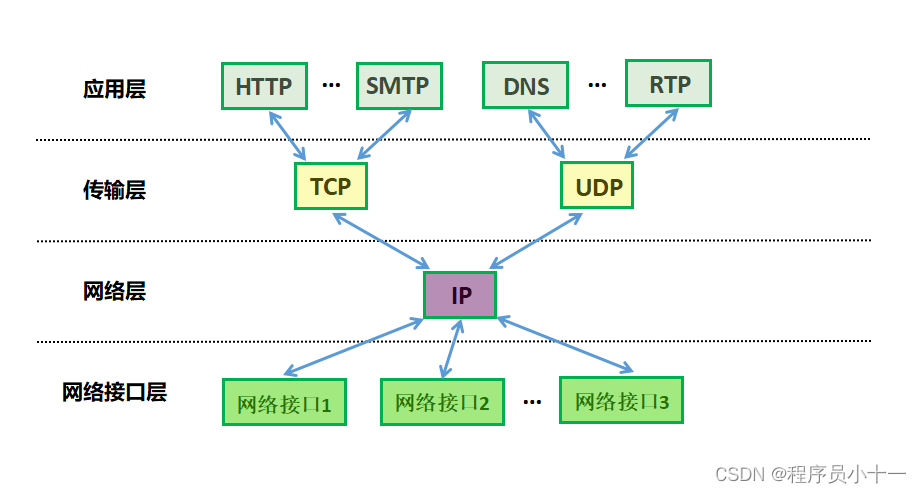
四、沙漏计时器形状的TCP/IP协议族
五、两种国际标准对比

- 国际标准 OSI参考模型并没有得到广泛认可。
- TCP/IP四层参考模型现在获得了广泛的应用。
- TCP/IP参考模型常被称为事实上的国际标准。
相似之处
- 两模型均基于独立协议栈
- 每一层的功能也大体相同
不同之处
- 服务、协议、接口不同
- 协议和模型的关系不同
- 有连接/无连接服务不同
- 协议的具体实现不同
