日本巨乳真人做的视频网站宣传推广的形式有哪些
在过去,服务区公厕常常给人留下脏乱差的印象,成为人们在长途旅行途中不愿停留的地方。然而,随着智慧科技的不断发展和应用,智慧公厕系统的出现改变了人们对服务区公厕的看法,为公共卫生设施的提升注入了新的活力。

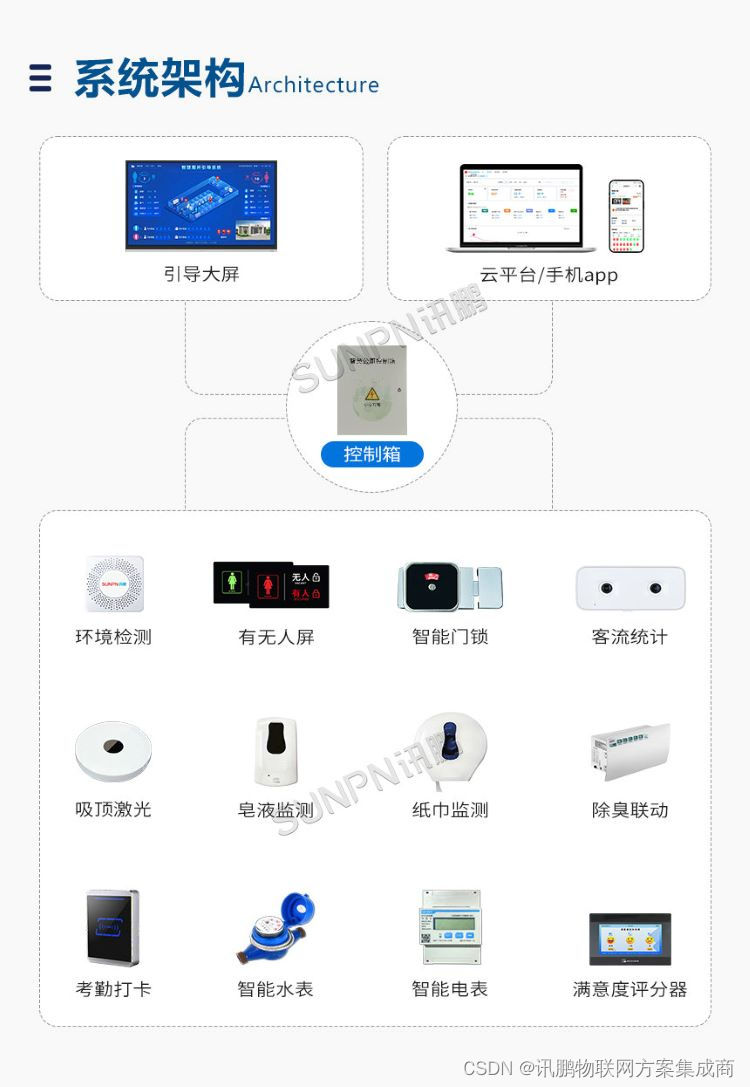
一、智慧公厕系统利用先进的科技手段,实现了公厕的智能化管理和运营。
通过智慧公厕系统智能感知设备,可以实现对公厕的实时监控,包括人流量、环境卫生情况等数据的收集和分析。这种实时监控不仅可以提高公厕的管理效率,也可以为用户提供更好的使用体验。用户可以通过手机App查询公厕的实时卫生状况,选择最近的干净卫生的公厕前往,避免了以往在选择公厕时碰到卫生问题的尴尬局面。

二、智慧公厕系统还提供了智能预约功能
用户可以提前在手机上预约使用公厕的时间,避免排队等候的情况发生。预约功能的出现不仅提升了公厕的使用效率,也提升了用户的体验感,让人们在使用公厕时更加方便快捷。

三、智慧公厕系统还加入了一系列人性化的设计
如自动洗手液、座圈冲洗、暖风烘干等功能,为人们提供了更加舒适、便利的使用体验。这些人性化的设计让公厕不再只是简单的厕所设施,更像是一个为人们提供舒适体验的公共服务设施。

随着智慧公厕系统的不断普及和应用,人们对服务区公厕的看法也在逐渐改变。以往被视为脏乱差的公厕,如今成为了一个兼具高科技和人性化服务的公共设施,受到了更多人的欢迎和喜爱。人们在长途旅行途中,不再抱怨公厕的环境卫生问题,反而会因为智慧公厕系统的便利和舒适而对服务区公厕刮目相看,乐意在此休息放松。
总的来说,智慧公厕系统的出现不仅提升了公共卫生设施的管理水平和服务质量,也改变了人们对服务区公厕的看法,让公厕不再是人们心中的“禁地”,而是一个值得信赖和赞誉的公共服务场所。随着智慧技术的不断发展和应用,相信未来的公共卫生设施将会更加智能化、人性化,为人们的生活带来更多便利和舒适。
【LCY】
