零一云主机网站改版seo建议
【一,概述】
这个是中型PLC
【二,外观】

网口编号:
【2】【3】 //默认ip:192.168.1.xxx
【0】【1】

 可视化授权不如禾川Q系。
可视化授权不如禾川Q系。
【三,总线轴】

因为本次带的轴是台达A2系列伺服
A2最快总线是【1ms】的倍数
ASD-A2-1521-EN 这里N表示比普通版多支持【雷尼绍】编码器,ECMC系列电机
在B3和A3版本上,已经支持雷尼绍编码器了,所以省略了N标记。可以用B3伺服直接带ECMC电机。
总线伺服使能会报【AL3E2】故障
AL3E2故障是同步帧过多

同步帧配置是【Sync0】
所以需要减少这个帧,这里设置比总线节拍,慢10倍


设置慢10倍,调试无问题。但设置慢16倍,电机来回打顿。
参数设置合理,下面就可以正常调试了。

【补充】
P2-08=10 恢复出厂设置【要重新上电】
此时伺服会急停报警AL13
这里我不需要外部io,所以把io全关掉
P2-10=100 常开-无功能【di1】
P2-11=100 常开-无功能【di2】
P2-12=100 常开-无功能【di3】
P2-13=100 常开-无功能【di4】124 原点
P2-14=100 常开-无功能【di5】022 常闭负限位
P2-15=100 常开-无功能【di6】023 常闭正限位
P2-16=100 常开-无功能【di7】021 常闭急停
P2-17=100 常开-无功能【di8】
重新启动PLC,复位伺服就能正常工作了。
【四,轴调试】
光轴能动还不行。
还需要用厂家的软件配置齿轮比,惯量,刚性等
伺服好了之后,还需要配置软件齿轮比。


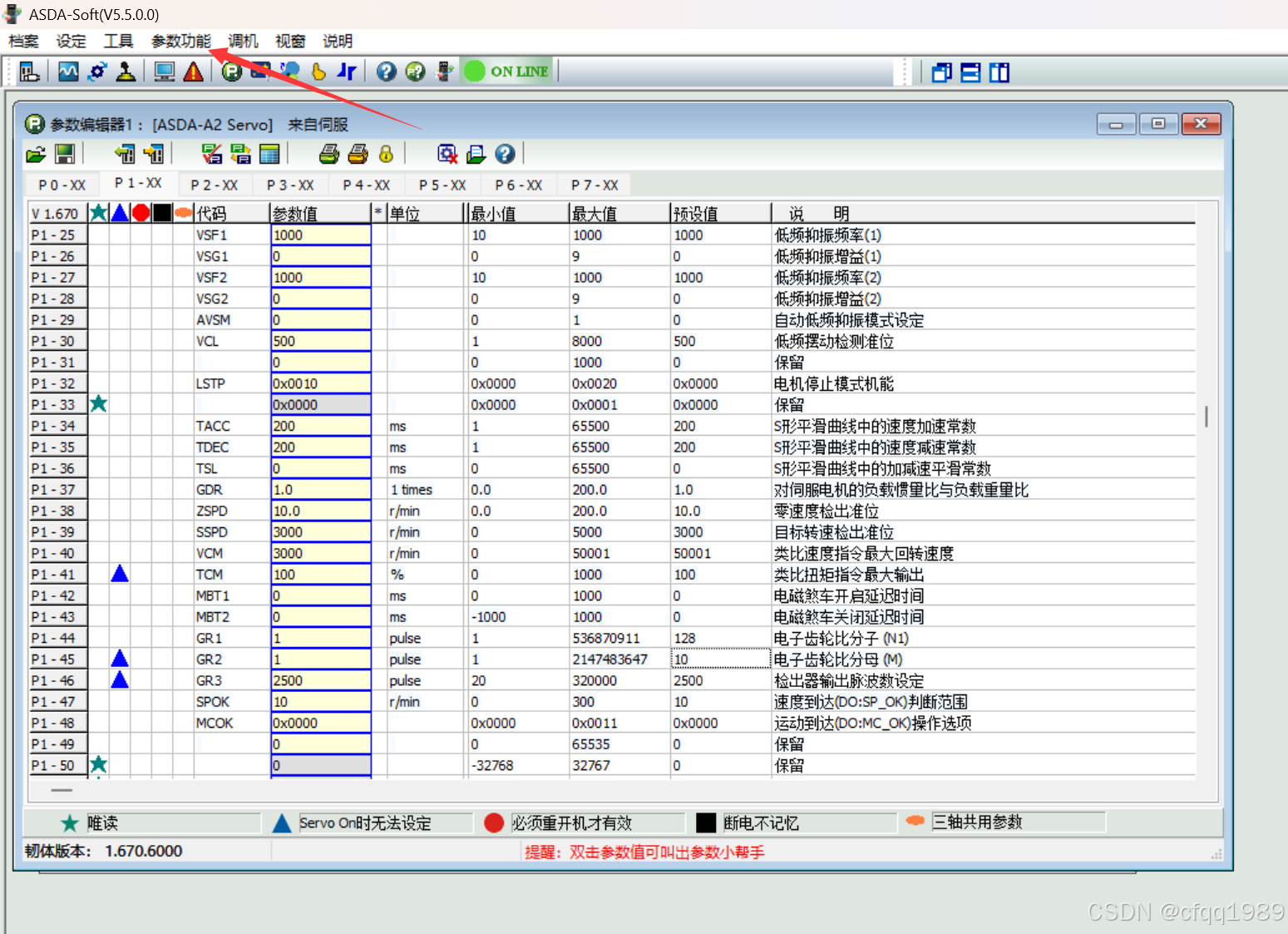
高版本不支持A2,所以用V5.5的版本

手动旋转测试

伺服参数
P1-44和P1-45 是电子齿轮比