白鹭引擎做h5网站一个网站如何推广
本文 我们来说harmonyos中的一种应用模型
Stage模型
官方提供了两种模型 一种是早期的 FA模型 另一种就是就是 harmonyos 3.1才开始的新增的一种模型 Stage模型
目前来讲 Stage 会成为现在乃至将来 长期推进的一种模型
也就是 无论是 现在的harmonyos 4.0 乃至 之后要发布的 harmonyos next 都会建议我们通过 Stage模型开发
本文呢 我们先来看一下Stage模型基本的一个概念
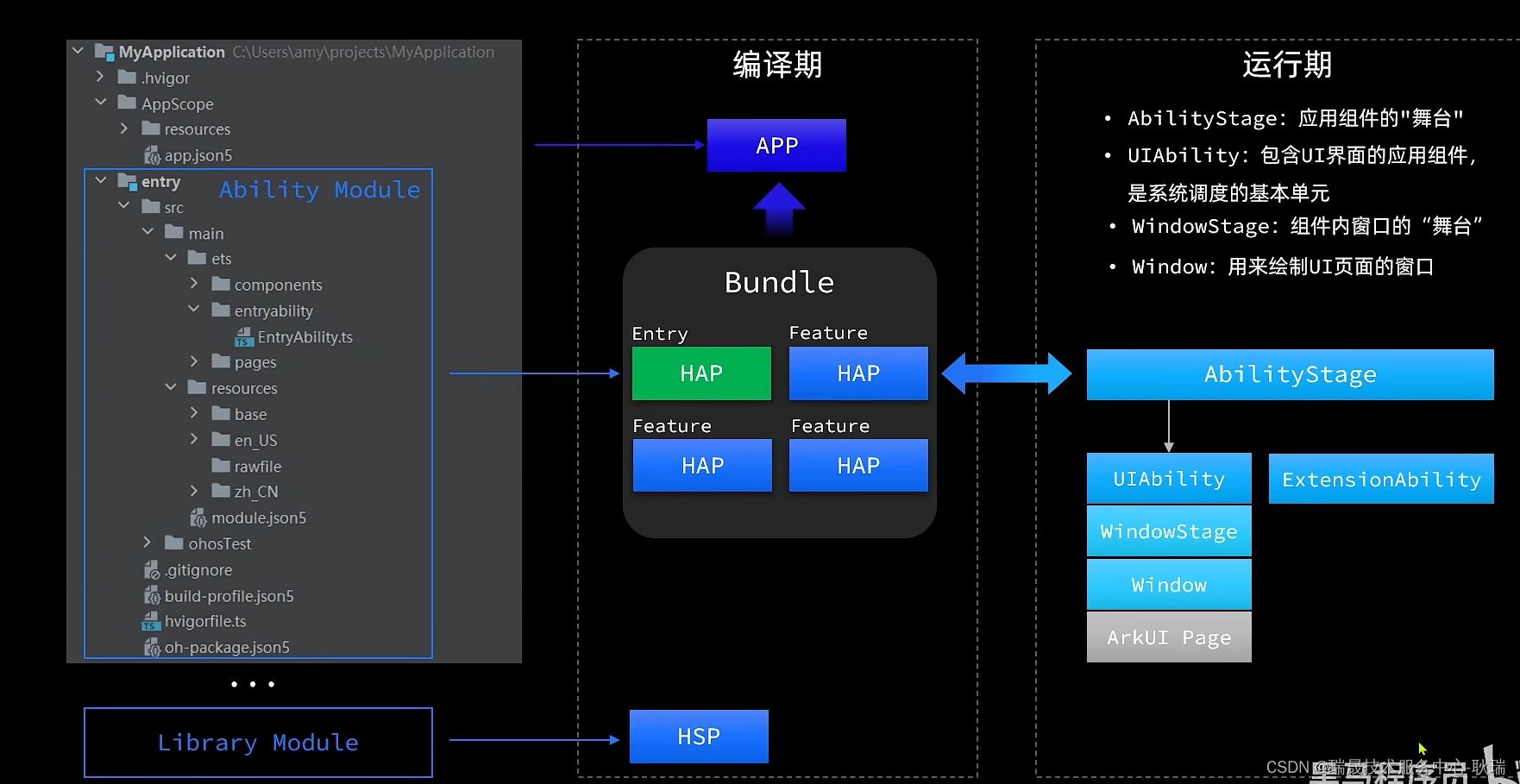
首先 我们项目里都会有一个 entry 子模块
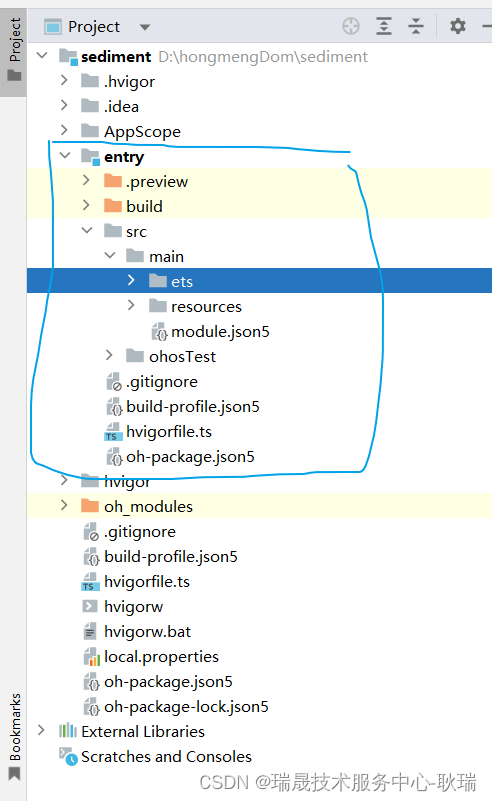
模块是应用的基本单元
它里面就会包含源代码 还有一些资源 以及一些配置文件之类的
那其实想这样的模块 我们在一个应用中还可以创建很多很多
但模块基本来讲,还是就分成两大类
第一类就像我们 entry这样 用来开发我们应用的一些能力的
像这样的 我们就称作 Ability Module
顾名思义 能力模块
一个应用的内部它的能力有很多很多,我们就可以把不同的能力 放到不同的模块开发
比如 大家很熟悉的微信

一个社交类的应用 它的核心功能其实就是社交嘛
那其中 聊天啊 朋友圈啊 好友啊 其实这些都可以分成一个社交类
这部分能力就可以放到同一个模块中
那后来 随着微信的发展 它有出来了一些新的功能 例如小程序呀 视频号呀等等
这些能力相互之间也都是独立的
所以 他们也都可以放在独立的 Ability Module 里面去
这样一来 我们整个应用的能力就都清晰的划分出来了
管理起来也非常的方便
这些属于一类 Ability Module
这些过程当中呢 他们就会有一些通用的 工具 资源 或者组件等等
那如果这些模块,大家都各自去开发,显然是一种重复和浪费
所以 我们就可以把重用的东西抽取出来,放到一个单独的模块里去
这种模块我们就称作 Library Module
顾名思义 就是 一种共享的依赖模块
那么 他们之间 Ability Module 就可以去引用 Library Module
然后 我们回到编辑器
我们选择根目录右键 选择New 就可以看到 module 模块选项了
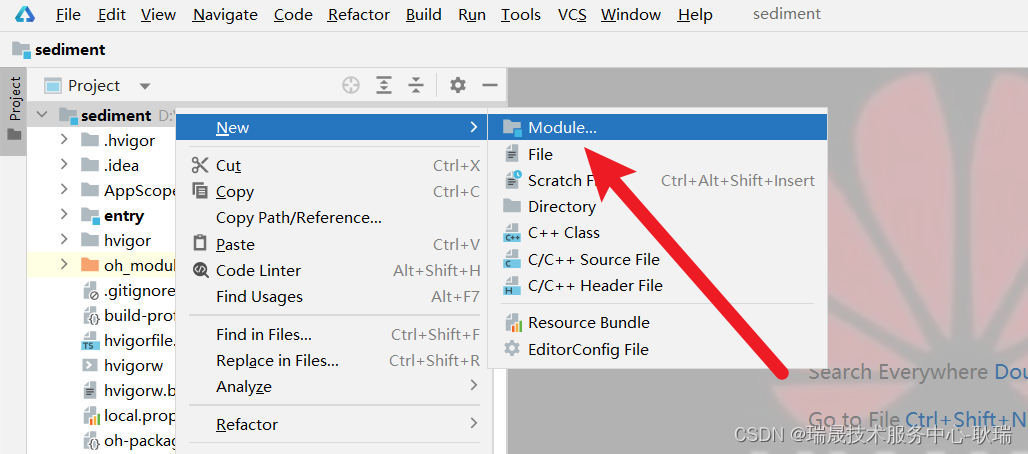
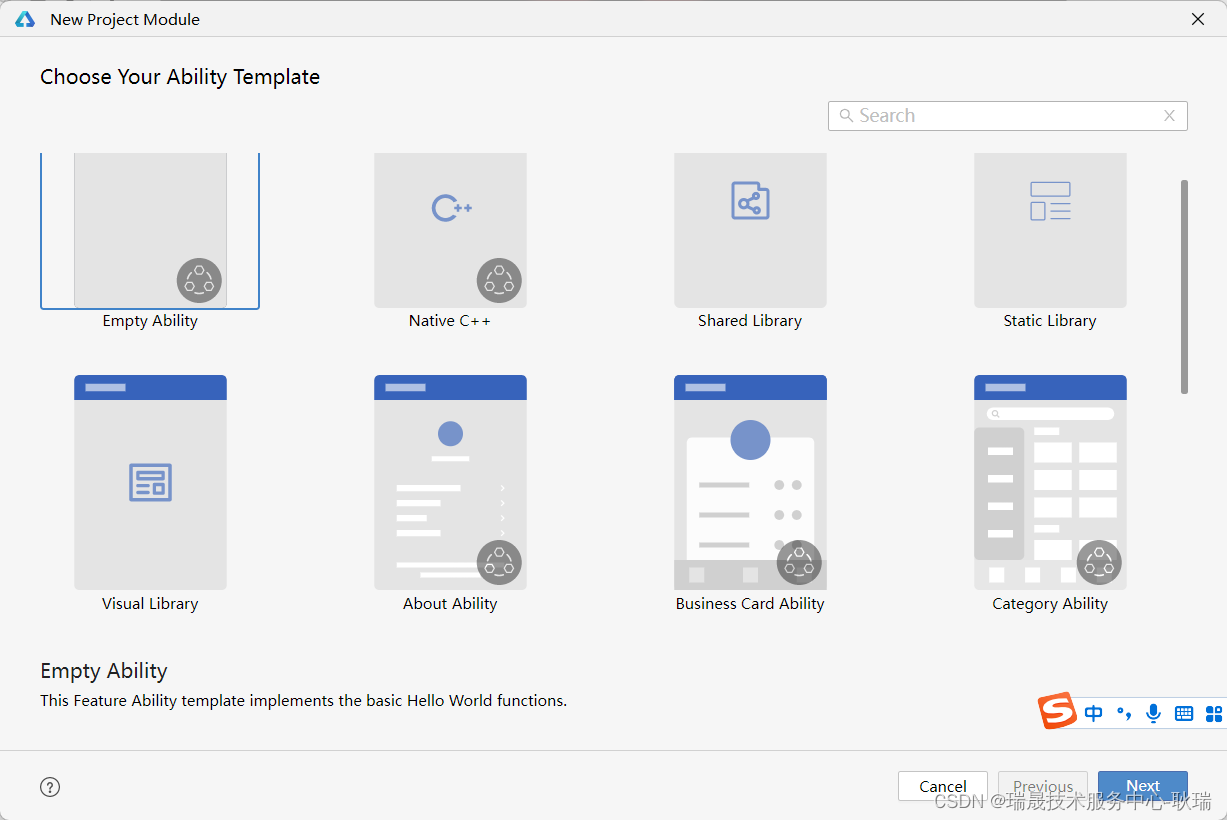
点击之后 我们这里就会有这种 module 的各种模板
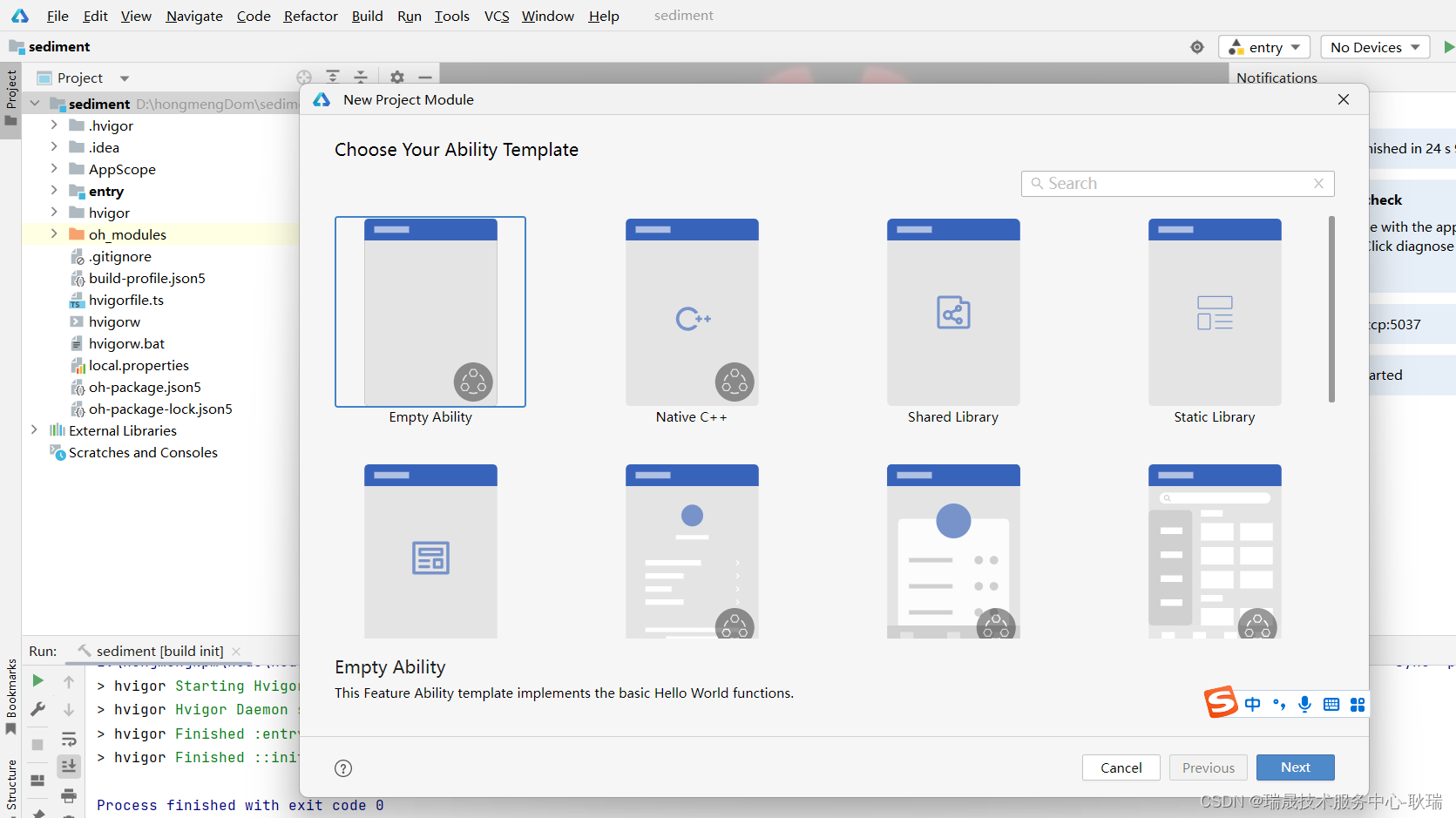
其实这么多 无法就是分成 Ability和Library
那么 这就是Stage模型创建的一个基本的项目结构了
但这是源码 最后整个项目还是会被打包成一个安装包
只是在Stage模型中 为了降低不同模块之间的耦合 每一个模块都可以独立编译或运行的
那么之后所有Ability类型的模块,将来就会被编译成 .HAP 格式的文件
但我们一个App那肯定只能有一个入口呀,对不对?
那么 当我们有多个HAP文件时 那么就要设置一个入口文件 我们将它称之为 Entry 类型的HAP文件
其他就可以理解为一些拓展功能 叫 Feature类型的 HAP
简单说 一个项目只能有一个 Entry类型的HAP 因为你没办法给一个app多个入口,但是呢 可以有多个Feature 拓展功能可以一直往后加呀
最终 我们所有的HAP 肯定还是都要合并到一个app中的
合并到一起之后 我们称之为 Bundle
那么 我们可以设置一个 Bundle
Bundle 会有一个name属性 我们可以给它一个独立标识
最后 Bundle 合并在一起 就是一个app安装包
而且 最大的好处是 首先 Entry 肯定是要的 跑不掉 但其他模块 可以选择性的安装
这样 你就可以让应用没那么大 以及提高安装效率
首先,我们知道,每一个HAP都是可以独立运行的,它在运行时 为了展示我们的界面和一些逻辑
它都会创建一个 AbilityStage 实例 AbilityStage 在这里 被我们翻译为应用组件能力的舞台
这个舞台的意思就很明显了,应用展示自己能力的地方。
AbilityStage 最常见的就是
ExtensionAbility和UIAbility
UIAbility 它是 包含UI界面的应用组件,是系统调度的基本单元。
UIAbility内部会先有一个Windowstage 简单说 就是一个窗口 在这个窗口中展示我们的UI界面