个人域名备案网站名称什么是网络营销策划
redis可视工具AnotherRedisDesktopManager的使用
简介
Another Redis DeskTop Manager 是一个开源项目,提供了以可视化的方式管理 Redis 的功能,可供免费下载安装,也可以在此基础上进行二次开发,主要特点有:
- 支持 Windows 平台和 MacOS 平台
- 支持查询 Key、查看单个 Key、Redis 运行状态
- 支持 String、List、Hash、Set、Zset 类型的可视化添加、修改与删除
下载安装
gitee下载地址:https://gitee.com/qishibo/AnotherRedisDesktopManager
下载对应版本并安装,macm1下载对应的dmg安装包

如果通过brew或者dmg安装后无法打开,报错不受信任或者移到垃圾箱,执行下面命令后再启动即可:
sudo xattr -rd com.apple.quarantine /Applications/Another\ Redis\ Desktop\ Manager.app
使用
新建连接

地址:Redis服务端地址
端口:默认 6379
密码:设置的Redis密码
连接名称:所新建连接的名称,不填会根据地址和端口自动生成
可能报错:Redis Client On Error: ReplyError: WRONGPASS invalid username-password pair or user is disabled. Config right?
解决方法:不写用户名!!!
查看连接
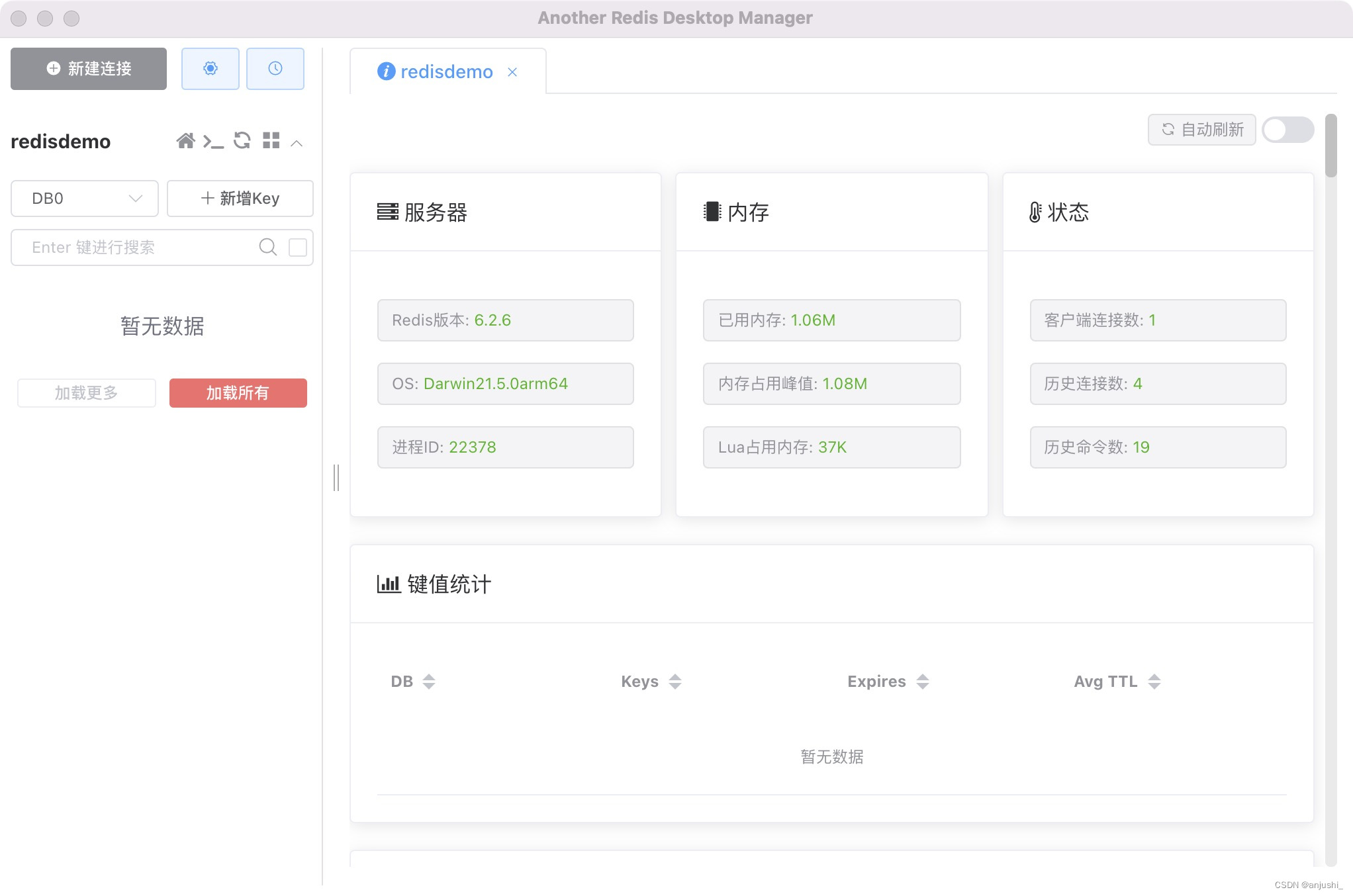
添加数据
点击新增key,添加键值对数据,设置键名和选择值类型,设置键名为uid


一般情况下,不会直接在可视化工具中进行添加数据等操作,而是通过业务代码对Redis进行操作,可视化工具用来查看数据。在可视化工具操作数据一般用于业务测试。
应用设置

