php装修公司网站源码申请域名的方法和流程
目录
第一步:创建一个空仓库
第二步:找到你想上传的文件所在的地址,打开命令窗口,git init
第三步:git add 想上传的文件 ,git commit -m "给这次提交取个名字"
第四步:和咱们在第一步创建的空仓库关联起来
第五步:git push -u origin master把当前分支 master 推送到远程仓库
第一步:创建一个空仓库

右上角加号,新建一个空仓库。
如果不是空仓库,比如有个README文件什么的,到时候可能要考虑合并时有冲突的问题。(Gitee:我这里明明有个README,你传过来的却没有README,你对README做了什么?我还要不要保留README?啊,算了,报个冲突让人类自己想办法吧)
第二步:找到你想上传的文件所在的地址,打开命令窗口,git init
如图,我想传一些Python文件到仓库里去,就在这些文件的父目录:“ 新建文件夹 ” 这个文件夹下,右键打开命令窗口。(那个.git文件夹就是执行 git init 后的效果)

对对,就这个 Git Bash Here。什么,没有?那你走错了,去隔壁看安装教程再来哦(挥手┏(^0^)┛)

输入git init。

注意:只有一次git init。如果你上传的是一个文件夹,不小心在文件夹的里面又git init了,会报错哦。
第三步:git add 想上传的文件 ,git commit -m "给这次提交取个名字"
我这里想把所有.py结尾的文件都上传,可以简写成*.py。(举一反三:*.java,*.c什么的,可以自己摸索一哈)
commit命令里的 -m 选项是为了在命令行中提供提交注释,就是可以给这次提交取个名字或者编个版本号来区分这次提交,不然以后提交得多了,没有注释就看不出来是哪次提交了。

第四步:和咱们在第一步创建的空仓库关联起来
先来看两个命令:
- git remote add:添加远程仓库
- git remote:查看当前的远程仓库
我们先要得到这个远程仓库的网址啊,follow me!

在这呢,这有个HTTPS地址,可以复制,但是啊,命令行不支持粘贴。所以要么记一记,要么用工具给它钉在窗口上抄写下来哦,如下图:

origin 是给这个地址起的别名,别名随便起。查看的时候也是显示别名,看着简洁一些。
让我看看有没有人报错,反正我报了:

404,找不到远程仓库,那应该是网址抄错了。不知道你们是为啥,反正我是因为地址太长,没写全。往后拉一拉,是以git结尾的地址哦

第五步:git push -u origin master把当前分支 master 推送到远程仓库
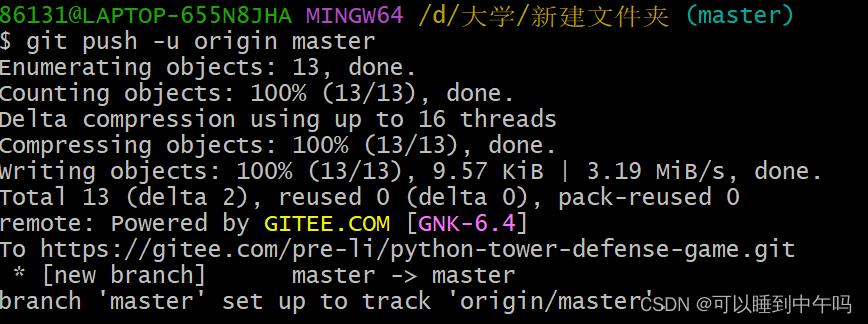
如果远程仓库不是空的,应该先执行这个命令:git pull --rebase origin master
git pull: 从远程分支拉取代码,可以得到远程分支上最新的代码。
git rebase是远程代码合并的一种方式,它和另一种方式git merge的区别:
- git merge将远端master的代码和本地的代码在新增的节点合并,之前的提交会分开去显示。
- git --rebase会将两个分支融合成一个线性的提交,不会形成新的节点。
总之就是git rebase更不容易产生冲突
产生冲突如何解决
在rebase的过程中,有时也会有冲突,这时Git会停止rebase并让用户去解决冲突,解决完冲突后,用git add命令去更新这些内容,然后不用执行git-commit,直接执行git rebase --continue,这样git会继续apply余下的补丁。
好了,到这里就完了。这里讲的都是基本基本的步骤,想要完全理解怎么回事最好还是多看看其他文章,多多使用这个工具,拜拜。
