全球建站新网站应该怎么做seo
一、进程与线程
进程
-
程序由指令和数据组成,但这些指令要运行,数据要读写,就必须将指令加载至 CPU,数据加载至内存。在指令运行过程中还需要用到磁盘、网络等设备。进程就是用来加载指令、管理内存、管理 IO 的
-
当一个程序被运行,从磁盘加载这个程序的代码至内存,这时就开启了一个进程。
-
进程就可以视为程序的一个实例。大部分程序可以同时运行多个实例进程(例如记事本、画图、浏览器等),也有的程序只能启动一个实例进程(例如网易云音乐、360 安全卫士等)
线程
-
一个进程之内可以分为一到多个线程。
-
一个线程就是一个指令流,将指令流中的一条条指令以一定的顺序交给 CPU 执行
-
Java 中,线程作为最小调度单位,进程作为资源分配的最小单位。 在 windows 中进程是不活动的,只是作为线程的容器
二者对比
-
进程基本上相互独立的,而线程存在于进程内,是进程的一个子集
-
进程拥有共享的资源,如内存空间等,供其内部的线程共享
-
进程间通信较为复杂
-
同一台计算机的进程通信称为 IPC(Inter-process communication)
-
不同计算机之间的进程通信,需要通过网络,并遵守共同的协议,例如 HTTP
-
-
线程通信相对简单,因为它们共享进程内的内存,一个例子是多个线程可以访问同一个共享变量
-
线程更轻量,线程上下文切换成本一般上要比进程上下文切换低
二、并行与并发
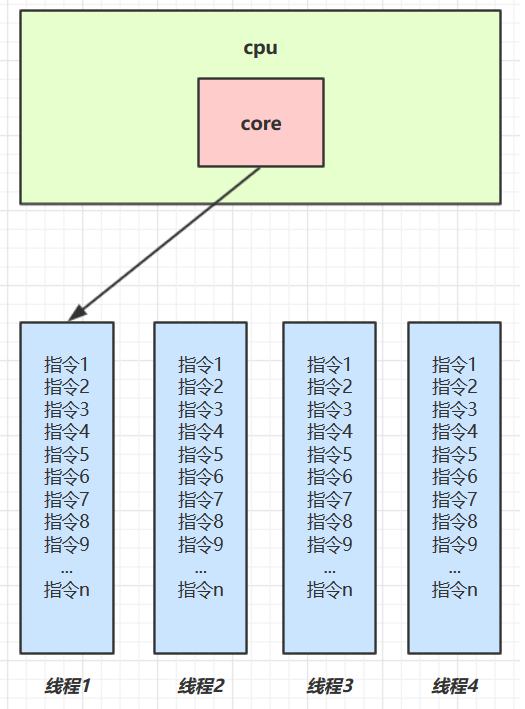
单核 cpu 下,线程实际还是 串行执行 的。操作系统中有一个组件叫做任务调度器,将 cpu 的时间片(windows 下时间片最小约为 15 毫秒)分给不同的线程使用,只是由于 cpu 在线程间(时间片很短)的切换非常快,人类感觉是 同时运行的 。总结为一句话就是:微观串行,宏观并行,
一般会将这种 线程轮流使用 CPU 的做法称为并发,对应的英文单词为 concurrent
| CPU | 时间片 1 | 时间片 2 | 时间片 3 | 时间片 4 |
|---|---|---|---|---|
| core | 线程 1 | 线程 2 | 线程 3 | 线程 4 |
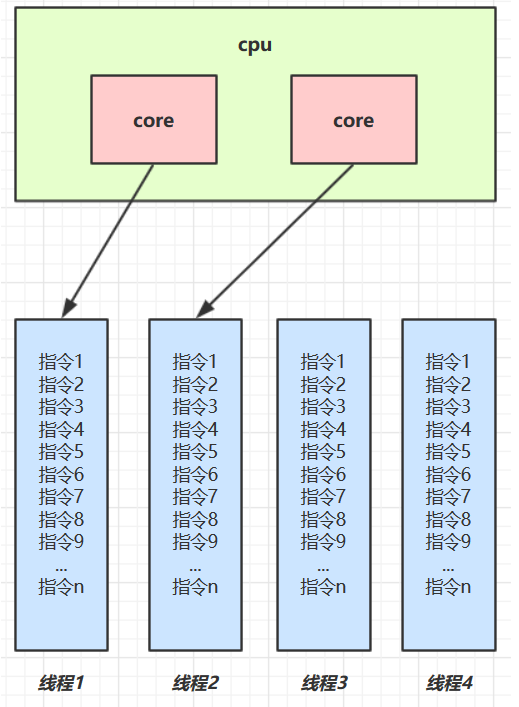
多核 cpu下,每个 核(core)都可以调度运行线程,这时候线程可以是并行的。对应的英文为parallel。在时间片1中,线程1与线程2可以同一时间执行。
| CPU | 时间片 1 | 时间片 2 | 时间片 3 | 时间片 4 |
|---|---|---|---|---|
| core 1 | 线程 1 | 线程 1 | 线程 3 | 线程 3 |
| core 2 | 线程 2 | 线程 4 | 线程 2 | 线程 4 |
引用 Rob Pike 的一段描述:
-
并发(concurrent)是同一时间应对(dealing with)多件事情的能力
-
并行(parallel)是同一时间动手做(doing)多件事情的能力
例子
-
家庭主妇做饭、打扫卫生、给孩子喂奶,她一个人轮流交替做这多件事,这时就是并发
-
家庭主妇雇了个保姆,她们一起这些事,这时既有并发,也有并行
-
保姆做饭,主妇喂奶,并行
-
保姆做饭、打扫卫生,并发
-
-
雇了3个保姆,一个专做饭、一个专打扫卫生、一个专喂奶,互不干扰,这时是并行
-
在实际的应用过程中一般既有并发也有并行。
