漳州本地网公司网站seo公司
文章目录
- 1. 模块简介
- 3. API接口
- 4. 功能介绍
- 4.1. 驱动状态机
- 4.2. Normal定时器
- 4.2.1. Channel状态机
- 4.2.2. 定时模式
- 4.2.3. 已启动时间和待溢出时间获取
- 4.3. 预定义定时器
- 5. 序列图
- 5.1. Continues Mode
- 5.2. One-Shot Mode
- 5.3. Disable/Enable Notifications
- 5.4. Wakeup
1. 模块简介
GPT驱动位于微控制器抽象层(MCAL)。该驱动负责初始化和控制微控制器内部的通用定时器(GTM的TOM/ATOM 或GTP12)。
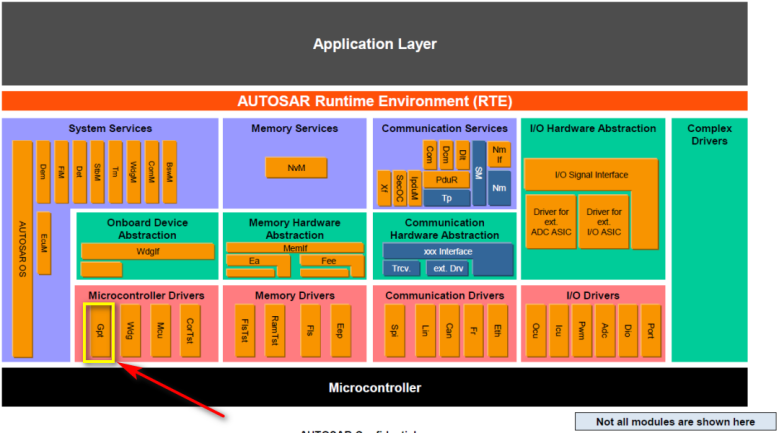
3.2.主要功能
- 支持启动/停止硬件定时器,支持单次(One-Shot)和连续(Continuous)两种模式
- 支持使能/禁止通道中断通知;
- 支持使能/禁止唤醒中断
- 支持1us和100us预定义定时器,用于时间服务模块,也可用于时间测量、超时检测等
- 支持获取定时器启动时间(Gpt_GetTimeElapsed)和待溢出时间(Gpt_GetTimeRemaining)
- 支持中断通知,定时器溢出后触发回调函数
- 支持定时器唤醒功能,用于ECU从低功耗模式恢复
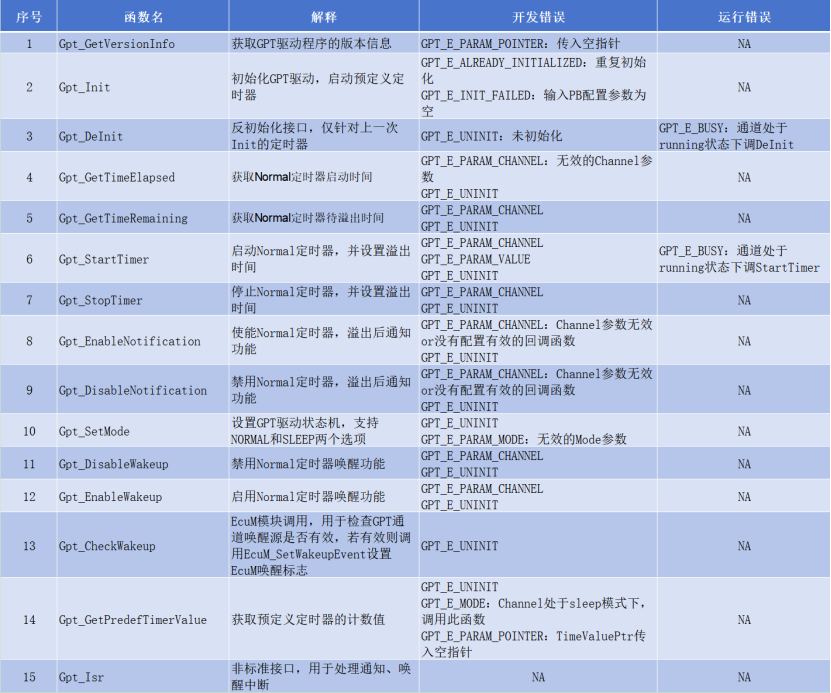
3. API接口
4. 功能介绍
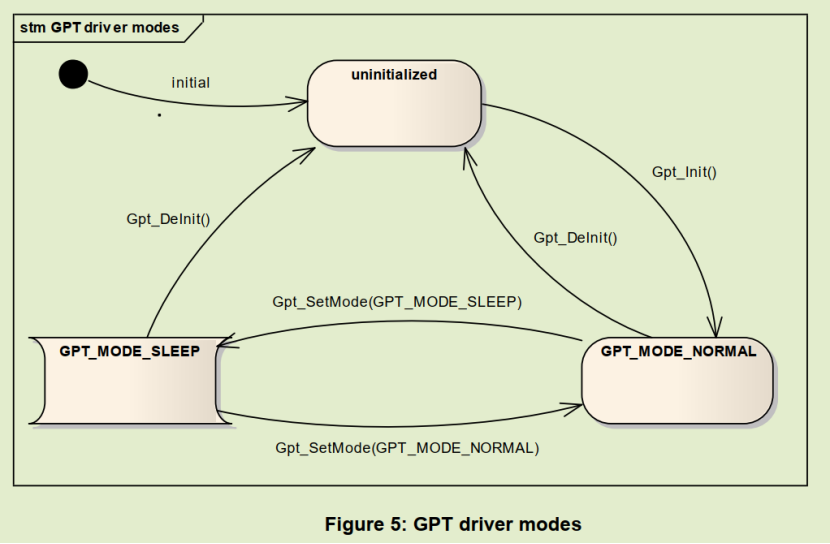
4.1. 驱动状态机
主要关注Normal和Sleep两个核心状态,Gpt模块的基本功能,比如单次 or 连续触发定时中断,预定义定时器等功能均需要在Normal模式下才能使用。Sleep模式需配合EcuM模块进行使用,实现最终系统级的唤醒功能。
4.2. Normal定时器
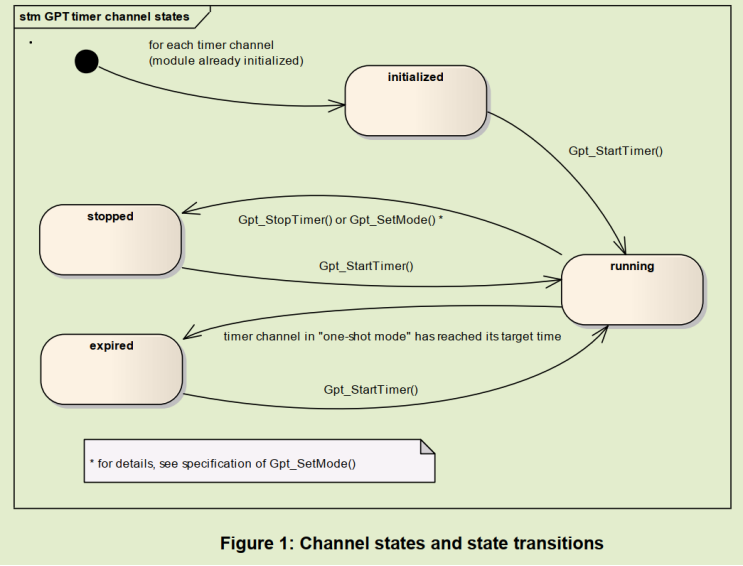
4.2.1. Channel状态机
4.2.2. 定时模式
对于Normal类型的定时器支持One-Shot或Continue两种模式。可通过Gpt_StartTimer和Gpt_StopTimer启动或停止定时器。
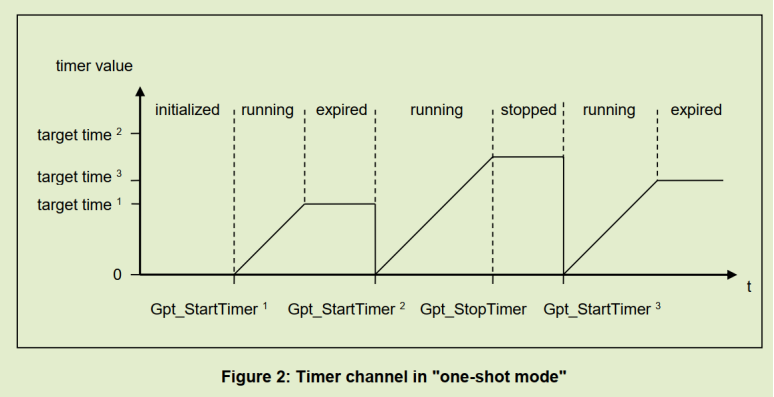
One-Shot模式下,计数到溢出值后,自动停止定时器,并保持计数值不变,通过Gpt_StartTimer启动定时器,定时器切换到running状态,并从0开始计数,溢出后,切换到expired状态,若使能通知,则触发中断函数并调用对应定时器的回调函数。
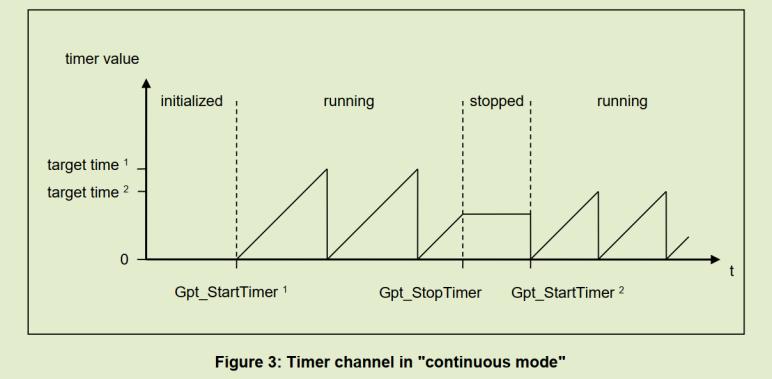
Continue模式下,启动后,定时器按Gpt_StartTimer设置的溢出值周期计数, 直到调用Gpt_StopTimer停止计数器或GTP切换到SLEEP模式。
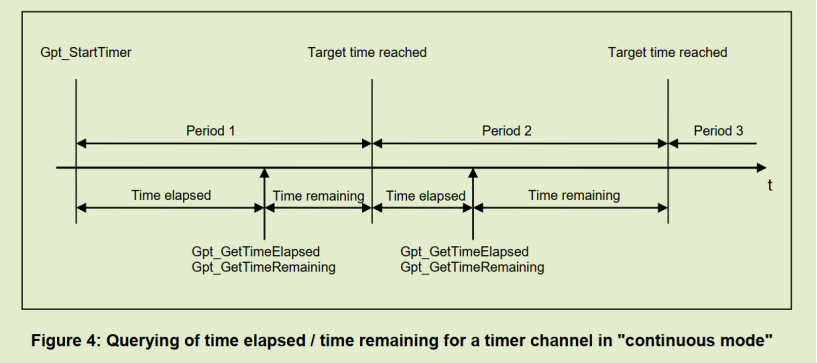
4.2.3. 已启动时间和待溢出时间获取
GTP提供Gpt_GetTimeElapsed、Gpt_GetTimeRemaining两个接口用于Normal定时器指定时间和待溢出时间。
Gpt_GetTimeElapsed在不同通道状态下的返回值和开发错误如下:
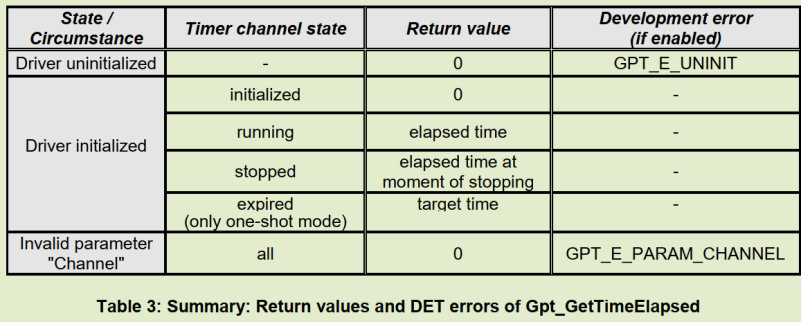
Gpt_GetTimeRemaining在不同通道状态下的返回值和开发错误如下:
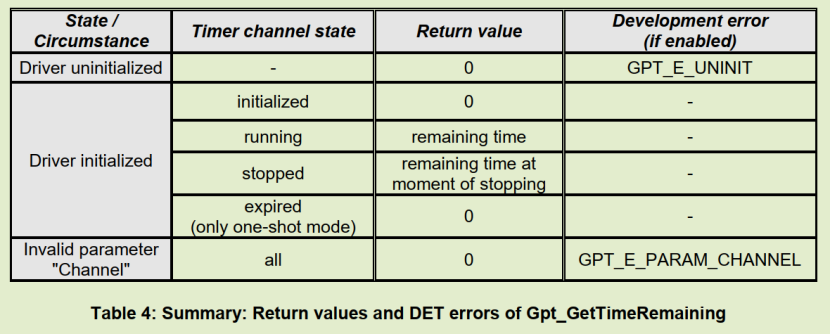
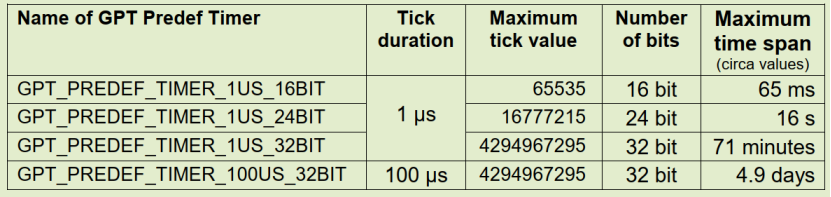
4.3. 预定义定时器
Gpt支持根据分辨率和定时器宽度分为四类预定义定时器,具体如下:
5. 序列图
Normal定时器具体模式、相应接口(不含预定义定时器)具体使用示例如下:
5.1. Continues Mode
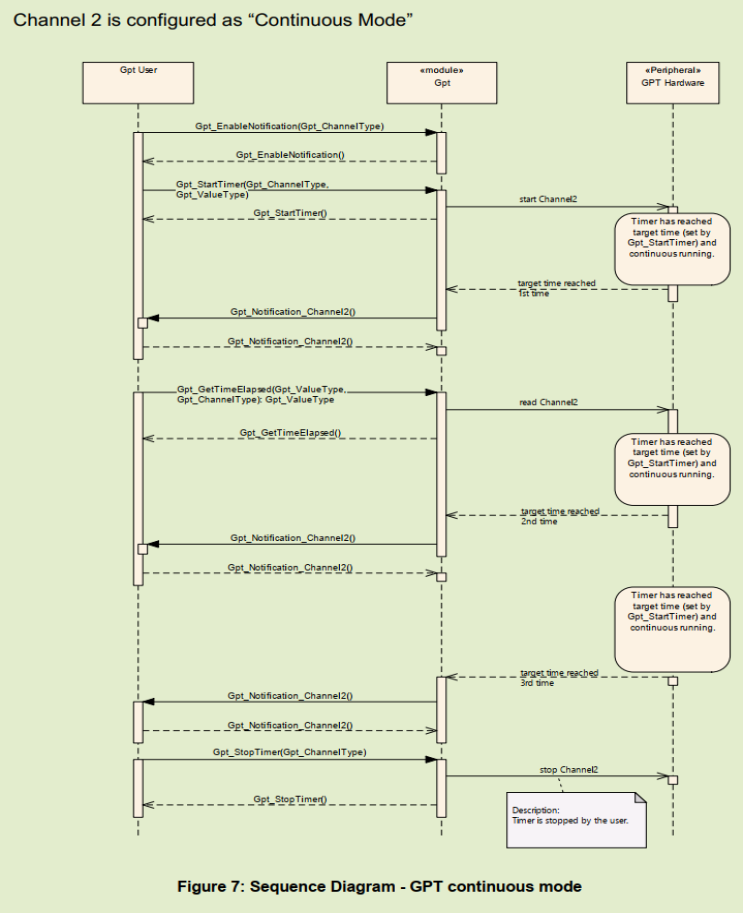
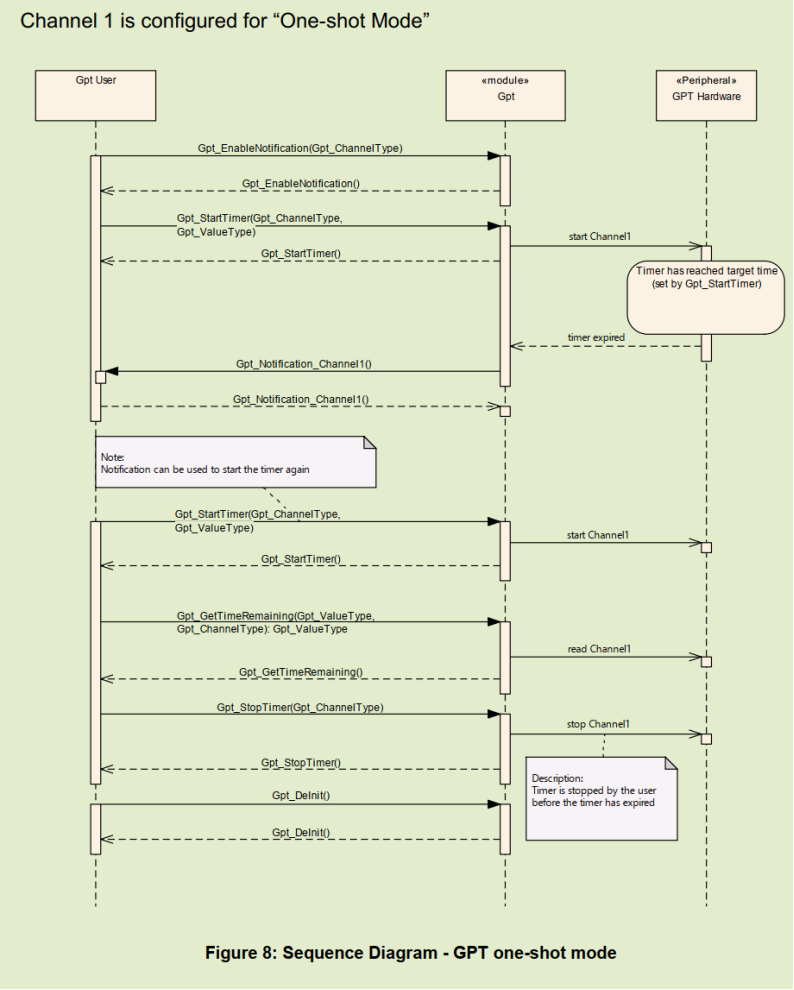
5.2. One-Shot Mode
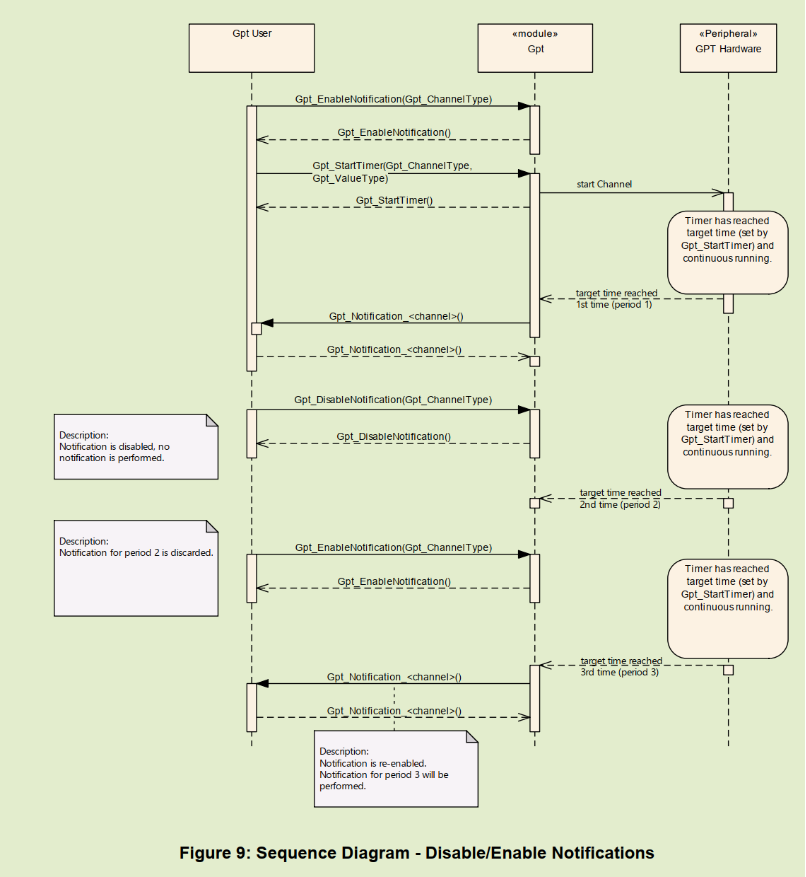
5.3. Disable/Enable Notifications
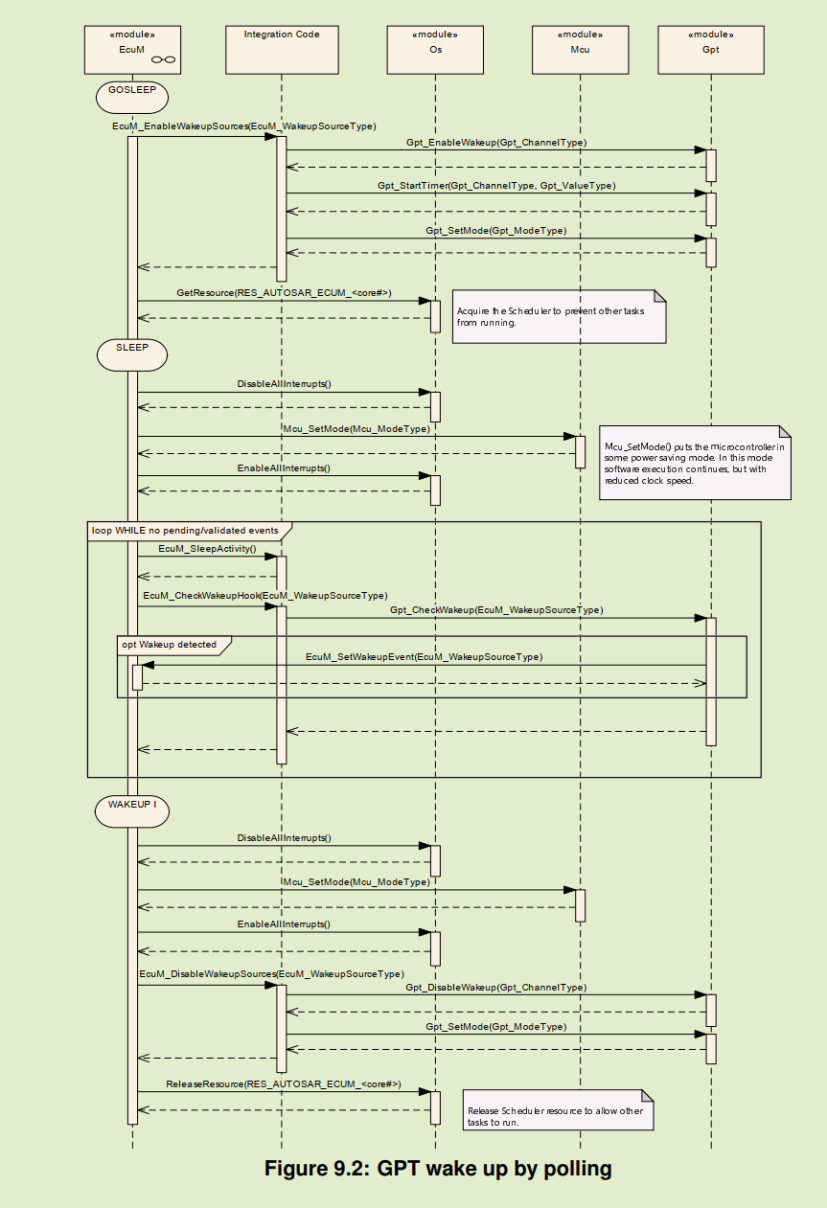
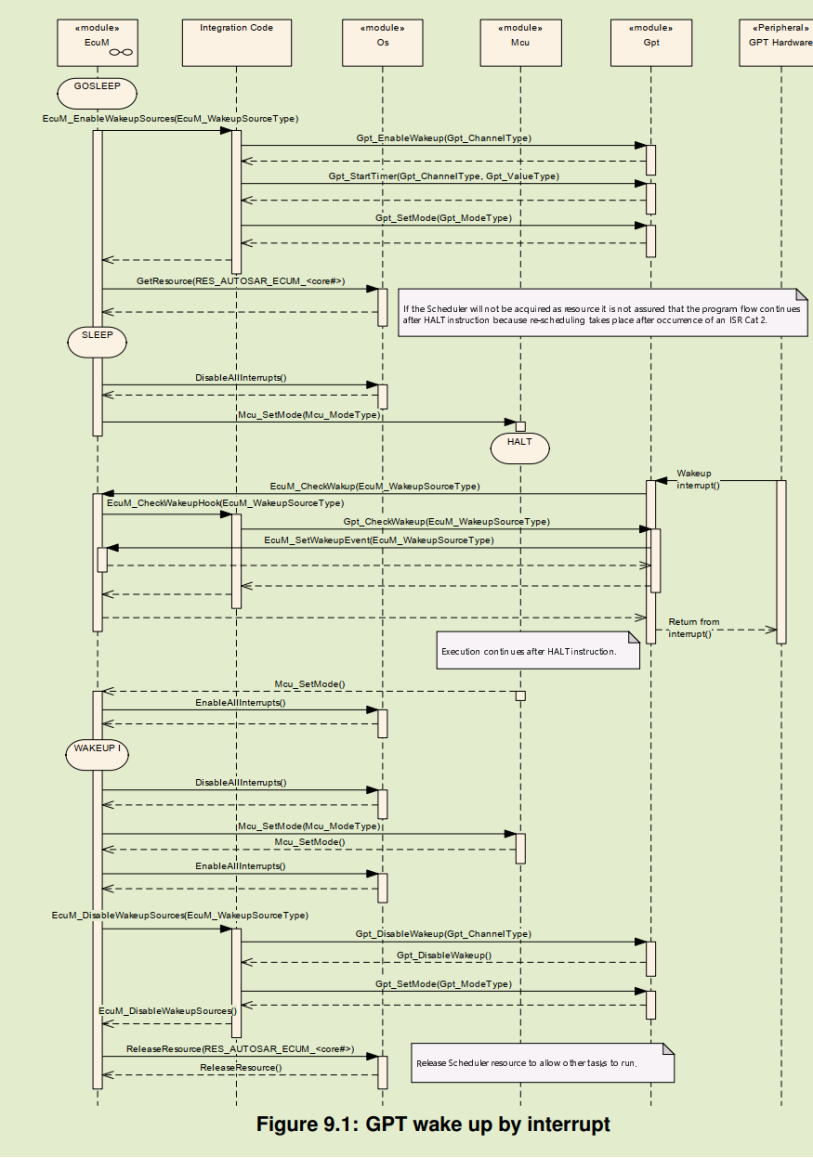
5.4. Wakeup
实际配合EcuM模块进行使用,在EcuM中提供中断和轮询两种方式进行处理,中断方式如下:
轮询流程如下: