南京网站优化公司百度指数是免费的吗
目录
场景
解决方案
解决思路
代码示例
代码改造
Java实现迭代器
迭代器模式的优点
思考
何时选用
场景
大公司收购了一个小公司,大公司的工资系统采用List来记录工资列表,而小公司是采用数组,老板希望通过决策辅助系统来统一查看工资数据不想看到两份不同的工资表。
解析:如何能够以一个统一的方式 来访问 内部实现不同的 聚合对象
解决方案
迭代器模式
定义:

所谓聚合就是指一组对象的组合结构:比如 Java中的集合、数组等
解决思路
要有一个统一的方式来访问,那就要定义这个统一的访问方式,那么按照统一的访问方式定义出来的接口就应该是Iterator接口。(定义访问和遍历元素的接口)
迭代器迭代的是具体的聚合对象,不同的聚合对象应该有不同的迭代器,所以应该抽象出来一个公共的父类,让它提供 操作聚合对象的 公共接口。也是就Aggregate对象(聚合对象)
如何创建?由于迭代器与聚合对象紧密相关,因此让具体的聚合对象来负责创建相应的迭代器对象
代码示例
工资实体
package day13迭代器模式.entity;/*** 工资实体*/
public class PayModel {/*** 支付工资的人员*/private String userName;/*** 支付的工资数额*/private double pay;public String getUserName() {return userName;}public void setUserName(String userName) {this.userName = userName;}public double getPay() {return pay;}public void setPay(double pay) {this.pay = pay;}@Overridepublic String toString() {return "PayModel{" +"userName='" + userName + '\'' +", pay=" + pay +'}';}
}
大公司原有的工资管理对象 使用List
package day13迭代器模式;import day13迭代器模式.entity.PayModel;import java.util.ArrayList;
import java.util.List;/*** 大公司原有的工资管理对象*/
public class PayDa {/*** 聚合对象*/private List list = new ArrayList();/*** 获取工资列表* @return 工资列表*/public List getPayList(){return list;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");list.add(payModel);list.add(payModel1);}
}
小公司原有的工资管理对象 使用数组
package day13迭代器模式;import day13迭代器模式.entity.PayModel;import java.util.ArrayList;
import java.util.List;/*** 小公司原有的工资管理对象*/
public class PayXiao {/*** 用数组管理*/private PayModel[] pms = null;/*** 获取工资列表* @return 工资列表*/public PayModel[] getPays(){return pms;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");pms = new PayModel[2];pms[0] = payModel;pms[1] = payModel1;}
}
Client
package day13迭代器模式;import day13迭代器模式.entity.PayModel;import java.util.Collection;
import java.util.Iterator;
import java.util.List;public class Client {public static void main(String[] args) {// 访问集团的工资列表PayDa payDa = new PayDa();// 先计算再获取payDa.calcPay();List payList = payDa.getPayList();Iterator it = payList.iterator();System.out.println("大公司工资列表: ");while (it.hasNext()){PayModel next = (PayModel)it.next();System.out.println(next);}// 访问小公司的工资列表PayXiao payXiao = new PayXiao();payXiao.calcPay();PayModel[] pays = payXiao.getPays();System.out.println("小公司工资列表: ");for (int i = 0; i < pays.length; i++) {System.out.println(pays[i]);}}
}

发现他们的访问方式是完全不一样的(一个是list,一个是对象数组)。
要使用迭代器来整合上面两个聚合对象,那就需要先定义出抽象的聚合对象和迭代器接口来,再提供相应的实现
代码改造
Iterator
package day13迭代器模式;public interface Iterator {/*** 移动到聚合对象的第一个位置*/public void first();/*** 移动到聚合对象的下一个位置*/public void next();/*** 判断是否移动到聚合对象的最后一个位置* @return true表示已经移动到聚合对象的最后一个位置* false表示没有移动到聚合对象的最后一个位置*/public boolean isDone();/*** 获取迭代的当前元素* @return 迭代的当前元素*/public Object currentItem();
}
定义好统一接口后,就得分别实现,一个是List实现,一个是数组实现
数组实现
package day13迭代器模式.Iterator;import day13迭代器模式.PayXiao;/*** 用来实现访问数组的迭代接口*/
public class ArrayIteratorImpl implements Iterator{/*** 用来存放被迭代的聚合对象*/private PayXiao payXiao = null;/*** 用来记录当前迭代到的位置索引* -1表示刚开始的时候,迭代器指向聚合对象第一个对象之前*/private int index = -1;/*** 构造函数,传入聚合对象*/public ArrayIteratorImpl(PayXiao payXiao){this.payXiao = payXiao;}@Overridepublic void first() {index = 0;}@Overridepublic void next() {if (index < this.payXiao.size()){index = index + 1;}}@Overridepublic boolean isDone() {if (index == this.payXiao.size()){return true;}return false;}@Overridepublic Object currentItem() {return this.payXiao.get(index);}
}
集合实现
package day13迭代器模式.Iterator;import day13迭代器模式.PayDa;public class CollectionIteratorImpl implements Iterator{/*** 用来存放被迭代的聚合对象*/private PayDa payDa = null;/*** 用来记录当前迭代到的位置索引* -1表示刚开始的时候,迭代器指向聚合对象第一个对象之前*/private int index = -1;/*** 构造函数,传入聚合对象*/public CollectionIteratorImpl(PayDa payDa){this.payDa = payDa;}@Overridepublic void first() {index = 0;}@Overridepublic void next() {if (index < this.payDa.size()){index = index + 1;}}@Overridepublic boolean isDone() {if (index == this.payDa.size()){return true;}return false;}@Overridepublic Object currentItem() {return this.payDa.get(index);}
}
迭代器迭代的是具体的聚合对象,不同的聚合对象应该有不同的迭代器,所以应该抽象出来一个公共的父类,让它提供 操作聚合对象的 公共接口。
也是就Aggregate对象(聚合对象)
package day13迭代器模式;import day13迭代器模式.Iterator.Iterator;/*** 迭代器迭代的是具体的聚合对象,不同的聚合对象应该有不同的迭代器,* 所以应该抽象出来一个公共的父类,让它提供 操作聚合对象的 公共接口。* 也是就Aggregate对象(聚合对象)*/
public abstract class Aggregate {/*** 工厂方法,创建对应迭代器对象的接口*/public abstract Iterator createIterator();
}
让PayDa和PayXiao,这两个原有的工资管理对象继承这个Aggregate
PayDa
package day13迭代器模式;import day13迭代器模式.Iterator.CollectionIteratorImpl;
import day13迭代器模式.Iterator.Iterator;
import day13迭代器模式.entity.PayModel;import java.util.ArrayList;
import java.util.List;/*** 大公司原有的工资管理对象*/
public class PayDa extends Aggregate{/*** 聚合对象*/private List list = new ArrayList();/*** 获取工资列表* @return 工资列表*/public List getPayList(){return list;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");list.add(payModel);list.add(payModel1);}@Overridepublic Iterator createIterator() {return new CollectionIteratorImpl(this);}public Object get(int index){Object obj = null;if (index < this.list.size()){obj = this.list.get(index);}return obj;}public int size(){return this.list.size();}
}
PayXiao
package day13迭代器模式;import day13迭代器模式.Iterator.ArrayIteratorImpl;
import day13迭代器模式.Iterator.Iterator;
import day13迭代器模式.entity.PayModel;import java.util.ArrayList;
import java.util.List;/*** 小公司原有的工资管理对象*/
public class PayXiao extends Aggregate{/*** 用数组管理*/private PayModel[] pms = null;/*** 获取工资列表* @return 工资列表*/public PayModel[] getPays(){return pms;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");pms = new PayModel[2];pms[0] = payModel;pms[1] = payModel1;}@Overridepublic Iterator createIterator() {return new ArrayIteratorImpl(this);}public Object get(int index){Object obj = null;if (index < pms.length){obj = pms[index];}return obj;}public int size(){return this.pms.length;}
}
Client
package day13迭代器模式;import day13迭代器模式.entity.PayModel;import java.util.Collection;
import java.util.Iterator;
import java.util.List;public class Client {public static void main(String[] args) {// 访问集团的工资列表PayDa payDa = new PayDa();// 先计算再获取payDa.calcPay();
// List payList = payDa.getPayList();
// Iterator it = payList.iterator();System.out.println("大公司工资列表: ");
// while (it.hasNext()){
// PayModel next = (PayModel)it.next();
// System.out.println(next);
// }test(payDa.createIterator());// 访问小公司的工资列表PayXiao payXiao = new PayXiao();payXiao.calcPay();
// PayModel[] pays = payXiao.getPays();System.out.println("小公司工资列表: ");test(payXiao.createIterator());}private static void test(day13迭代器模式.Iterator.Iterator it){// 循环输出聚合对象中的值// 首先设置迭代器到第一个元素it.first();while (!it.isDone()){// 取出当前的元素来Object o = it.currentItem();System.out.println("当前元素: " + o);it.next();}}
}

迭代器模式的关键思想就是把聚合对象的遍历和访问从聚合对象中分离出来,放入单独的迭代器中。
Java实现迭代器
PayModel类(工资实体)
package day13迭代器Java实现.entity;/*** 工资实体*/
public class PayModel {/*** 支付工资的人员*/private String userName;/*** 支付的工资数额*/private double pay;public String getUserName() {return userName;}public void setUserName(String userName) {this.userName = userName;}public double getPay() {return pay;}public void setPay(double pay) {this.pay = pay;}@Overridepublic String toString() {return "PayModel{" +"userName='" + userName + '\'' +", pay=" + pay +'}';}
}
创建Aggregate,这里使用java.util.Iterator
package day13迭代器Java实现;import java.util.Iterator;/*** 迭代器迭代的是具体的聚合对象,不同的聚合对象应该有不同的迭代器,* 所以应该抽象出来一个公共的父类,让它提供 操作聚合对象的 公共接口。* 也是就Aggregate对象(聚合对象)*/
public abstract class Aggregate {/*** 工厂方法,创建对应迭代器对象的接口*/public abstract Iterator createIterator();
}
PayDa继承该抽象类
package day13迭代器Java实现;import day13迭代器Java实现.entity.PayModel;import java.util.ArrayList;
import java.util.Iterator;
import java.util.List;/*** 大公司原有的工资管理对象*/
public class PayDa extends Aggregate {/*** 聚合对象*/private List<PayModel> list = new ArrayList<PayModel>();/*** 获取工资列表* @return 工资列表*/public List<PayModel> getPayList(){return list;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");list.add(payModel);list.add(payModel1);}@Overridepublic Iterator createIterator() {return list.iterator();}}
PayXiao继承该抽象类
package day13迭代器Java实现;import day13迭代器Java实现.Iterator.ArrayIteratorImpl;
import day13迭代器Java实现.entity.PayModel;import java.util.Iterator;/*** 小公司原有的工资管理对象*/
public class PayXiao extends Aggregate {/*** 用数组管理*/private PayModel[] pms = null;/*** 获取工资列表* @return 工资列表*/public PayModel[] getPays(){return pms;}/*** 计算工资*/public void calcPay(){// 计算工资并把工资数据填充到工资列表中// 为了测试,输入些数据进去PayModel payModel = new PayModel();payModel.setPay(3800);payModel.setUserName("张三");PayModel payModel1 = new PayModel();payModel1.setPay(5800);payModel1.setUserName("李四");pms = new PayModel[2];pms[0] = payModel;pms[1] = payModel1;}@Overridepublic Iterator createIterator() {return new ArrayIteratorImpl(this);}public Object get(int index){Object obj = null;if (index < pms.length){obj = pms[index];}return obj;}public int size(){return this.pms.length;}
}
将小公司的融入大公司,就让小公司来实现这个迭代器,让它进行统一
ArrayIteratorImpl
package day13迭代器Java实现.Iterator;import day13迭代器Java实现.PayXiao;import java.util.Iterator;/*** 用来实现访问数组的迭代接口*/
public class ArrayIteratorImpl implements Iterator {/*** 用来存放被迭代的聚合对象*/private PayXiao payXiao = null;/*** 用来记录当前迭代到的位置索引* -1表示刚开始的时候,迭代器指向聚合对象第一个对象之前*/private int index = 0;/*** 构造函数,传入聚合对象*/public ArrayIteratorImpl(PayXiao payXiao){this.payXiao = payXiao;}@Overridepublic void remove() {Iterator.super.remove();}/*** 判断是否还有下一个元素* @return*/@Overridepublic boolean hasNext() {if (payXiao != null && index < payXiao.size()){return true;}return false;}@Overridepublic Object next() {Object o = null;if (hasNext()){o = payXiao.get(index);// 每取走一个值,就把已访问索引加1index++;}return o;}
}
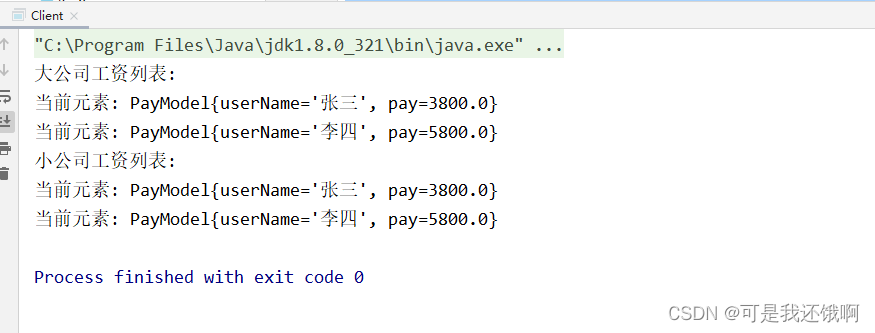
Client
package day13迭代器Java实现;import day13迭代器Java实现.entity.PayModel;import java.util.Iterator;public class Client {public static void main(String[] args) {// 访问集团的工资列表PayDa payDa = new PayDa();// 先计算再获取payDa.calcPay();
// List payList = payDa.getPayList();
// Iterator it = payList.iterator();System.out.println("大公司工资列表: ");
// while (it.hasNext()){
// PayModel next = (PayModel)it.next();
// System.out.println(next);
// }test(payDa.createIterator());// 访问小公司的工资列表PayXiao payXiao = new PayXiao();payXiao.calcPay();
// PayModel[] pays = payXiao.getPays();System.out.println("小公司工资列表: ");test(payXiao.createIterator());}private static void test(Iterator it){// 判断是否还有下一个元素while (it.hasNext()){PayModel next = (PayModel)it.next();System.out.println(next);}}
}

解析:为什么要保留数据的IteratorImpl呢?因为list有iterator方法可以直接调用,数组没有要进行转变,怎么转变呢?就是实现Iterator接口后重写方法next和hasNext这两个方法。以此来跟list相同就可以使用统一的迭代器了。
在Client中,大公司调用自身list的迭代器,小公司调用重写后的迭代器

它new了一个Impl,这个Impl实现的就是java.util.iterator的迭代器且重写了方法

迭代器模式的优点


思考
本质:
控制访问聚合对象中的元素
何时选用

