品牌网站建设开发价格站长工具seo客户端
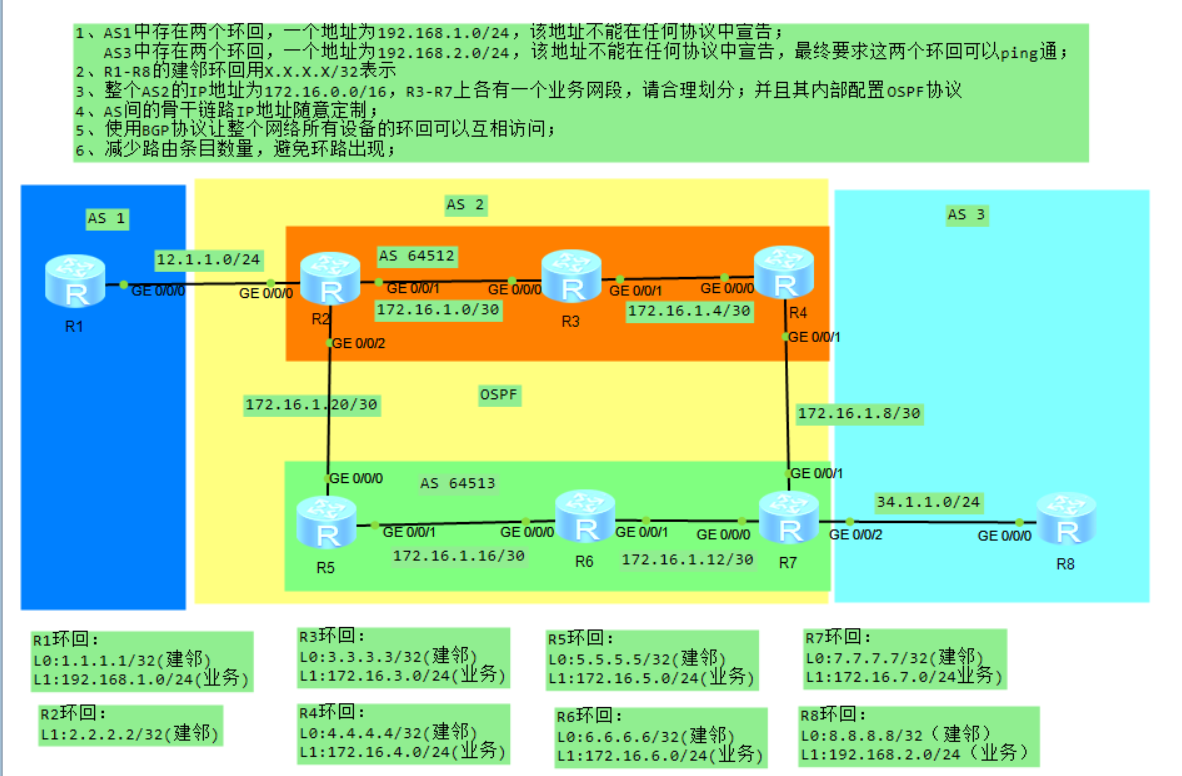
实验需求
1、AS1中存在两个环回,一个地址为192.168.1.0/24,该地址不能在任何协议中宣告;AS3中存在两个环回,一个地址为192.168.2.0/24,该地址不能在任何协议中宣告,最终要求这两个环回可以ping通;
2、R1-R8的建邻环回用x.x.x.x/32表示;整个AS2的IP地址为172.16.0.0/16,请合理划分;并且其内部配置OSPF协议;
3、AS间的骨干链路IP地址随意定制;
4、使用BGP协议让整个网络所有设备的环回可以互相访问;
5、减少路由条目数量,避免环路出现;
需求分析
1. AS1和AS3中的环回地址
要求:
AS1中有两个环回地址(192.168.1.0/24),这两个地址不能被任何协议(如BGP、OSPF等)宣告。
AS3中有两个环回地址(192.168.2.0/24),同样不能被任何协议宣告。
最终这两个环回地址需要能够ping通。
分析:
需要确保这两个地址不通过BGP或OSPF进行广告传播,应该在协议配置中排除它们的宣告。
可能需要通过静态路由或在路由策略中进行特殊配置,保证这些环回地址之间的连通性。
解决方案: 使用静态路由,或者通过BGP/OSPF策略控制这些地址的传播。BGP的network指令可以用来指定哪些网络可以被宣告,而不宣告这些环回地址。
2. R1-R8的环回地址
要求:
R1到R8之间的环回地址使用x.x.x.x/32表示。
对应的AS2的IP地址范围是172.16.0.0/16,需要合理划分该范围并配置OSPF。
分析:
每个路由器的环回地址可以被分配一个唯一的/32地址,用于进行OSPF的邻接建立。
解决方案: 在172.16.0.0/16的地址范围内,可以为每个路由器的环回接口划分一个独立的/32地址。OSPF的邻接可以通过环回地址建立,并且/32地址在OSPF中会被作为一个“可达的网络”进行传播。
3. AS间的骨干链路IP地址
要求:
骨干链路的IP地址可以随意定制。
分析:
骨干链路是连接不同AS的关键,IP地址可以灵活分配,确保网络之间的连通性即可。
解决方案: 可根据需要选择合适的IP地址范围,确保不同AS之间的路由能够顺利传递。一般情况下,可以选择私有地址段(如10.x.x.x、172.x.x.x、192.168.x.x)来作为骨干链路的地址。
4. 使用BGP协议实现环回互通
要求:
使用BGP协议让所有设备的环回接口可以互相访问。
分析:
BGP协议需要在AS间进行配置,广告环回地址。
解决方案: 在每个AS内配置BGP,使得各个AS的路由器能够通过BGP广告环回接口的地址,同时利用AS间的骨干链路互通。需要在BGP配置中合理设置network指令、路由过滤和策略等。
5. 减少路由条目数量,避免环路
要求:
尽量减少路由条目数量,避免路由环路的产生。
分析:
可以通过配置路由过滤(如BGP的prefix-list、route-map等)来限制某些路由的传递,避免不必要的路由条目。
使用OSPF的区域划分,限制路由传播范围,也有助于减少路由表的大小。
解决方案: 对BGP使用合理的策略,避免将不必要的网络广告出去,防止路由环路的出现;使用OSPF的区域划分(例如骨干区域、普通区域)来控制路由的传播。
实验过程:
配置IP和环路
[R1]int g0/0/0
[R1-GigabitEthernet0/0/0]ip add 12.1.1.1 24
[R1-GigabitEthernet0/0/0]int l0
[R1-LoopBack0]ip add 172.16.0.1 32
[R1-LoopBack0]int l1
[R1-LoopBack1]ip add 192.168.1.1 24
[R2]int g0/0/0
[R2-GigabitEthernet0/0/0]ip add 12.1.1.2 24
[R2-GigabitEthernet0/0/0]int g0/0/1
[R2-GigabitEthernet0/0/1]ip add 172.16.1.1 30
[R2-GigabitEthernet0/0/1]int g0/0/2
[R2-GigabitEthernet0/0/2]ip add 172.16.1.21 30
[R2-GigabitEthernet0/0/2]int l0
[R2-LoopBack0]ip add 172.16.0.2 32
[R3]int g0/0/0
[R3-GigabitEthernet0/0/0]ip add 172.16.1.2 30
[R3-GigabitEthernet0/0/0]int g0/0/1
[R3-GigabitEthernet0/0/1]ip add 172.16.1.5 30
[R3-GigabitEthernet0/0/1]int l0
[R3-LoopBack0]ip add 172.16.0.3 32
[R3-LoopBack0]int l1
[R3-LoopBack1]ip add 172.16.3.1 24
[R4]int g0/0/0
[R4-GigabitEthernet0/0/0]ip add 172.16.1.6 30
[R4-GigabitEthernet0/0/0]int g0/0/1
[R4-GigabitEthernet0/0/1]ip add 172.16.1.9 30
[R4-GigabitEthernet0/0/1]int l0
[R4-LoopBack0]ip add 172.16.0.4 32
[R4-LoopBack0]int l1
[R4-LoopBack1]ip add 172.16.4.1 24
[R5]int g0/0/0
[R5-GigabitEthernet0/0/0]ip add 172.16.1.22 30
[R5-GigabitEthernet0/0/0]int g0/0/1
[R5-GigabitEthernet0/0/1]ip add 172.16.1.17 30
[R5-GigabitEthernet0/0/1]int l0
[R5-LoopBack0]ip add 172.16.0.5 32
[R5-LoopBack0]int l1
[R5-LoopBack1]ip add 172.16.5.1 32
[R6]int g0/0/0
[R6-GigabitEthernet0/0/0]ip add 172.16.1.18 30
[R6-GigabitEthernet0/0/0]int g0/0/1
[R6-GigabitEthernet0/0/1]ip add 172.16.1.13 30
[R6-GigabitEthernet0/0/1]int l0
[R6-LoopBack0]ip add 172.16.0.6 32
[R6-LoopBack0]int l1
[R6-LoopBack1]ip add 172.16.6.1 24
[R7]int g0/0/0
[R7-GigabitEthernet0/0/0]ip add 172.16.1.14 30
[R7-GigabitEthernet0/0/0]int g0/0/1
[R7-GigabitEthernet0/0/1]ip add 172.16.1.10 30
[R7-GigabitEthernet0/0/1]int g0/0/2
[R7-GigabitEthernet0/0/2]ip add 34.1.1.7 24
[R7-GigabitEthernet0/0/2]int l0
[R7-LoopBack0]ip address 172.16.0.7 32
[R7-LoopBack0]int l1
[R7-LoopBack1]ip address 172.16.7.1 24
[R8]int g0/0/0
[R8-GigabitEthernet0/0/0]ip address 34.1.1.8 24
[R8-GigabitEthernet0/0/0]int l0
[R8-LoopBack0]ip add 172.16.0.8 32
[R8-LoopBack0]int l1
[R8-LoopBack1]ip add 192.168.2.1 24
ospf协议
[R2]ospf 1 router-id 2.2.2.2
[R2-ospf-1]a 0
[R2-ospf-1-area-0.0.0.0]network 172.16.0.2 0.0.0.0
[R2-ospf-1-area-0.0.0.0]network 172.16.1.0 0.0.0.3
[R2-ospf-1-area-0.0.0.0]network 172.16.1.20 0.0.0.3
[R3]ospf 1 router-id 3.3.3.3
[R3-ospf-1]a 0
[R3-ospf-1-area-0.0.0.0]network 172.16.1.0 0.0.0.3
[R3-ospf-1-area-0.0.0.0]network 172.16.1.4 0.0.0.3
[R3-ospf-1-area-0.0.0.0]network 172.16.0.3 0.0.0.0
[R3-ospf-1-area-0.0.0.0]network 172.16.3.0 0.0.0.255
[R4]ospf 1 router-id 4.4.4.4
[R4-ospf-1]a 0
[R4-ospf-1-area-0.0.0.0]network 172.16.0.4 0.0.0.0
[R4-ospf-1-area-0.0.0.0]network 172.16.1.4 0.0.0.3
[R4-ospf-1-area-0.0.0.0]network 172.16.1.8 0.0.0.3
[R4-ospf-1-area-0.0.0.0]network 172.16.4.0 0.0.0.255
[R5]ospf 1 router-id 5.5.5.5
[R5-ospf-1]a 0
[R5-ospf-1-area-0.0.0.0]network 172.16.1.20 0.0.0.3
[R5-ospf-1-area-0.0.0.0]network 172.16.1.16 0.0.0.3
[R5-ospf-1-area-0.0.0.0]network 172.16.0.5 0.0.0.0
[R5-ospf-1-area-0.0.0.0]network 172.16.5.0 0.0.0.255
[R6]ospf 1 router-id 6.6.6.6
[R6-ospf-1]a 0
[R6-ospf-1-area-0.0.0.0]network 172.16.0.6 0.0.0.0
[R6-ospf-1-area-0.0.0.0]network 172.16.1.12 0.0.0.3
[R6-ospf-1-area-0.0.0.0]network 172.16.1.16 0.0.0.3
[R6-ospf-1-area-0.0.0.0]network 172.16.6.0 0.0.0.255
[R7]ospf 1 router-id 7.7.7.7
[R7-ospf-1]a 0
[R7-ospf-1-area-0.0.0.0]network 172.16.0.7 0.0.0.0
[R7-ospf-1-area-0.0.0.0]network 172.16.1.8 0.0.0.3
[R7-ospf-1-area-0.0.0.0]network 172.16.1.12 0.0.0.3
[R7-ospf-1-area-0.0.0.0]network 172.16.7.0 0.0.0.255
BGP建邻
[R1]bgp 1
[R1-bgp]peer 12.1.1.2 as-number 2
[R2]bgp 64512
[R2-bgp]confederation id 2
[R2-bgp]confederation peer-as 64513
[R2-bgp]peer 12.1.1.1 as-number 1
[R2-bgp]peer 172.16.1.22 as-number 64513
[R2-bgp]peer 172.16.1.22 next-hop-local
[R5]bgp 64513
[R5-bgp]confederation id 2
[R5-bgp]confederation peer-as 64512
[R5-bgp]peer 172.16.1.21 as-number 64512
[R5-bgp]peer 172.16.1.21 next-hop-local
[R7]bgp 64513
[R7-bgp]peer 34.1.1.8 as-number 3
[R8]bgp 3
[R8-bgp]peer 34.1.1.7 as-number 2
IBGP建邻
[R2]bgp 64512
[R2-bgp]peer 172.16.0.3 as-number 64512
[R2-bgp]peer 172.16.0.3 connect-interface l0
[R2-bgp]peer 172.16.0.3 next-hop-local
[R3]bgp 64512
[R3-bgp]confederation id 2
[R3-bgp]peer 172.16.0.2 as-number 64512
[R3-bgp]peer 172.16.0.2 connect-interface l0
[R3-bgp]peer 172.16.0.4 as-number 64512
[R3-bgp]peer 172.16.0.4 connect-interface l0
[R4]bgp 64512
[R4-bgp]confederation id 2
[R4-bgp]peer 172.16.0.3 as-number 64512
[R4-bgp]peer 172.16.0.3 next-hop-local
[R5]bgp 64513
[R5-bgp]peer 172.16.0.6 as-number 64513
[R5-bgp]peer 172.16.0.6 connect-interface l0
[R5-bgp]peer 172.16.0.6 next-hop-local
[R6]bgp 64513
[R6-bgp]confederation id 2
[R6-bgp]peer 172.16.0.5 as-number 64513
[R6-bgp]peer 172.16.0.5 connect-interface l0
[R6-bgp]peer 172.16.0.7 as-number 64513
[R6-bgp]peer 172.16.0.7 connect-interface l0
[R7]bgp 64513
[R7-bgp]confederation id 2
[R7-bgp]peer 172.16.0.6 as-number 64513
[R7-bgp]peer 172.16.0.6 connect-interface l0
[R7-bgp]peer 172.16.0.6 next-hop-local
配置反射器
[R3-bgp]peer 172.16.0.4 reflect-client
[R6-bgp]peer 172.16.0.7 reflect-client
BGP宣告环回
[R2]ip route-static 172.16.0.0 16 NULL 0
[R2-bgp]network 172.16.0.0 16
[R7]ip route-static 172.16.0.0 16 NULL 0
[R7-bgp]network 172.16.0.0 16
R1 R8环回互访
[R1]interface Tunnel 0/0/0
[R1-Tunnel0/0/0]ip add 10.1.1.1 24
[R1-Tunnel0/0/0]tunnel-protocol gre
[R1-Tunnel0/0/0]source 172.16.0.1
[R1-Tunnel0/0/0]destination 172.16.0.8
[R1]ip route-static 192.168.2.0 24 10.1.1.2
[R8]int Tunnel 0/0/0
[R8-Tunnel0/0/0]ip address 10.1.1.2 24
[R8-Tunnel0/0/0]tunnel-protocol gre
[R8-Tunnel0/0/0]source 172.16.0.8
[R8-Tunnel0/0/0]destination 172.16.0.1
[R8]ip route-static 192.168.1.0 24 10.1.1.1
———————————————————————————————————————————
一、BGP路由选路原则(13条)
1. 丢弃下一跳(NEXT_HOP)不可达的路由。
2. 优选Preferred-value值最大的路由(默认0,取值0~65535,H3C和华为私有属性)。
3. 优选本地优先级(LOCAL_PREF)最高的路由。
4. 依次选择network命令生成的路由、import-route命令引入的路由、聚合路由。
5. 优选AS路径(AS_PATH)最短的路由。
6. 依次选择ORIGIN属性为IGP、EGP、Incomplete的路由。
7. 优选MED值最低的路由。
8. 依次选择从EBGP、联盟EBGP、联盟IBGP、IBGP学来的路由。
9. 优选下一跳度量值(通过IGP到达下一跳的度量)最低的路由。
10. 优选CLUSTER_LIST长度最短的路由。
11. 优选ORIGINATOR_ID最小的路由。
12. 优选Router ID最小的路由器发布的路由。
13. 优选IP地址最小的对等体发布的路由。
二、BGP负载分担时的选路
1. 背景:BGP默认选出唯一最优路由,可通过配置命令或路由策略修改属性实现负载分担,如 maximum load-balancing 2 允许最多2条等价路径。
2. 与IGP的区别:
- IGP通过自身路由算法,对度量值相等的路由进行负载分担。
- BGP无路由计算算法,基于选路规则有条件地实现负载分担。
三、BGP路由的发布策略
- 只将最优路由发布给对等体(默认发布BGP路由表最优路由,配置 active-route-advertise 则发布IP路由表最优路由)。
- 只发布自己使用的最优路由。
- 从EBGP获得的路由向所有BGP对等体发布。
- 从IBGP获得的路由不向IBGP对等体发布(IBGP水平分割),但会发布给EBGP对等体。
- BGP连接建立后,向新对等体发布所有满足条件的路由,后续仅在路由变化时发布更新。
四、BGP属性(控制选路的方法)
1. 公认属性(所有路由器必须识别)
公认必遵属性(BGP路由必须携带)
- AS_path:记录路由经过的AS编号,用于AS防环,选路时AS_PATH短的优先。
- next-hop:下一跳地址。向EBGP邻居发布路由时,下一跳为EBGP邻居地址;向IBGP邻居发布时,下一跳不变,可通过命令修改为本地地址。
- origin:描述路由来源,属性值优选顺序为IGP>EGP>Incomplete。
公认可选属性(所有路由器识别,非必须携带)
- local-perference:本地优先级,仅在IBGP邻居间传递,默认值100,值大的优先,用于AS内选择离开本AS的最佳路由。
- Atomic-aggregate:自动聚合属性,BGP支持自动或手动聚合。
2. 可选属性
可选传递属性(路由器可不识别,但会传递)
- aggregator:手动聚合属性。
- community:团体属性。
可选非传递属性(路由器可不识别,且不传递)
- clustor_list:集群列表。
- originator_id:集群ID。
- MED:多出口鉴别器,用于判断流量进入AS的最优路径,仅在相邻AS间传递,默认值0(network路由)或原IGP的cost(引入路由),值小的优先。
3. preferred-value
- 首选项,H3C和华为私有属性,默认0,取值0~65535,值大的路由优先。
五、属性控制的选择建议
1. 影响下游所有路由器选路:使用AS-PATH。
2. 影响本AS内部某个路由器选路:使用Local-preference。
3. 影响下游某一个AS的路由器选路:使用MED。
4. 影响某一台路由器选路:使用preferred-value。
六、属性控制方法
通过路由策略实现,对匹配的路由用 Apply 子句修改属性,在邻居的入/出方向调用策略,空节点允许其他网段通过。
BGP对等体组、聚合、路由反射器、联盟、团体属性
七、BGP协议特性
1. 负责在自治系统间传递路由,AS内部路由扩散依靠IGP。
2. 是路径矢量协议,一跳为一个自治系统,路由在AS间传递时下一跳会变化,在AS内部传递时下一跳不变。
3. 具有AS防环机制,通过AS_PATH属性,当路由的AS_PATH中包含本AS编号时不学习该路由。
4. 基于TCP协议传输,端口号179,需手动配置邻居。
5. 第一次网络收敛发送完整路由表,后续只发送增量更新。
6. 有多种属性可控制路由选择。
7. 支持路由聚合。
8. 可进行路由过滤和路由策略配置。
八、BGP基本术语
- BGP Speaker:运行BGP协议的路由器。
- BGP Peer:相互存在TCP连接、交换路由信息的BGP Speaker。
- BGP对等体:
- EBGP对等体:跨AS的邻居,一般物理直连,从其获得的路由会向所有对等体通告。
- IBGP对等体:同一AS内部的邻居。
- 邻居可以直连,也可以非直连。
九、BGP规划问题(路由黑洞)
- 产生原因:IBGP邻居之间存在未运行BGP协议的路由器,无法获得BGP路由,导致数据包被丢弃。
- 解决方法:
- BGP引入IGP。
- 在黑洞路由器上配置目的网段的静态路由。
- 建立IBGP全连接(存在IBGP水平分割机制,从IBGP邻居学习的路由不传递给其他IBGP邻居)。
- 使用BGP路由反射器(无视IBGP防环机制,减少邻居关系数量)。
- 采用BGP联盟(减少邻居关系数量,受IBGP水平分割限制)。
十、BGP环路问题(水平分割)
- EBGP水平分割:通过AS_PATH属性防环,学习到的路由中若有本地AS号则拒绝学习。
- IBGP水平分割:路由器从一个IBGP对等体学习到的BGP路由,不会通告给其他IBGP对等体。
十一、BGP消息种类
- 头部信息:包含标记(解决协议兼容性)、长度(指示报文长度)、类型(指示报文类型)。
- 数据包种类:
- Open:建立BGP对等体连接,携带route-id,包含保持时间、可选参数等。
- Keepalive:周期性发送以保持连接有效性,默认每60秒发送,超时时间180秒。
- Update:携带路由更新信息,包括要撤销和新增的路由及相关属性。
- Notification:检测到错误状态时发送,之后关闭BGP连接。
- Router-refresh:改变路由策略后,要求对等体重发指定地址族的完整路由表,仅支持该能力的路由器会响应。
十二、BGP状态机
- Idle:空闲状态,停留30秒,准备TCP连接并监视远程对等体。
- Connect:TCP连接中,连接失败进入Active状态。
- Active:TCP主动连接方,连接未成功则反复尝试。
- OpenSent:成功建立TCP连接,发送open报文,等待对方open报文。
- OpenConfirm:收到open报文,发送Keepalive报文,等待第一个Keepalive报文。
- Established:收到Keepalive报文,成功建立邻居关系。
十三、BGP邻居建立条件
- IBGP:
- 物理口建邻:建议使用直连接口地址。
- 环回口建邻:对方接口有IP地址且TCP可达,更新源地址需与指定邻居地址一致,无需直连。
- EBGP:
- 物理口建邻:建议使用直连接口地址。
- 环回口建邻:对方接口有IP地址且TCP可达,可修改最大跳数实现非直连,更新源地址需与指定邻居地址一致。
- 注意:默认IBGP邻居间数据包TTL为255,EBGP为1,环回建立EBGP邻居需修改TTL值。
十四、BGP基本配置
1. 启动与创建连接:启动BGP,配置router-id,指定对等体及AS号,创建地址族并使能交换路由信息能力。
2. 优化连接:指定建立TCP连接的源接口,设置EBGP对等体最大跳数。
3. 生成路由:将本地路由发布到BGP路由表,或引入其它路由协议的路由。
4. 查看命令:display bgp peer(查看对等体信息)、display bgp routing-table(查看路由表)。
